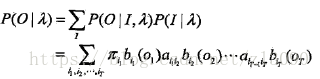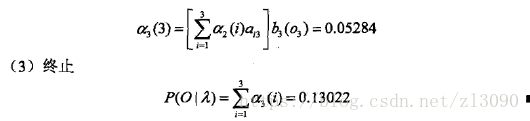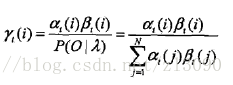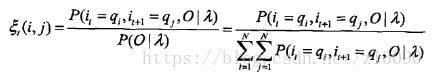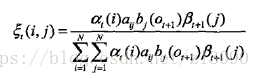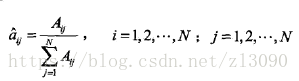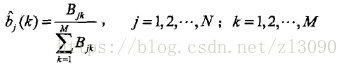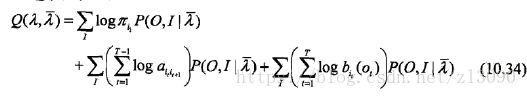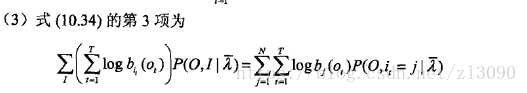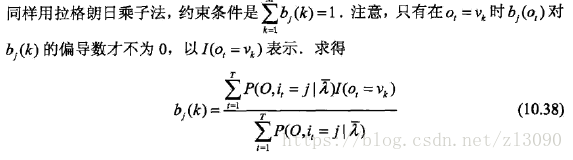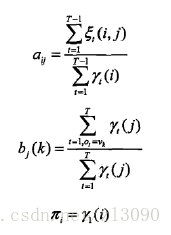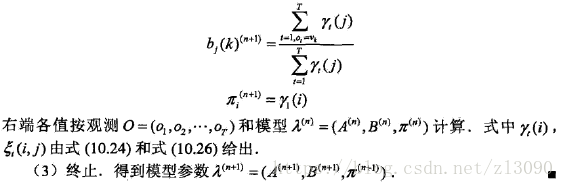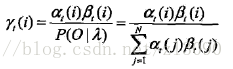【统计学习方法-李航-笔记总结】十、隐马尔可夫模型

本文是李航老师《统计学习方法》第十章的笔记，欢迎大佬巨佬们交流。

主要参考博客:

https://www.cnblogs.com/YongSun/p/4767667.html

https://www.cnblogs.com/naonaoling/p/5701634.html

https://www.cnblogs.com/fxjwind/p/3949993.html

主要内容：

1. 隐马尔可夫模型的基本概念

2. 概率计算算法

3. 学习算法

4. 预测算法

隐马尔可夫模型(hidden Markov model, HMM)是可用于标注问题的统计学习模型，标注问题的目的在于学习一个模型，使它能够对观测序列给出标记序列作为预测，HMM描述由隐藏的马尔可夫链随机生成观测序列的过程，属于生成模型。

1. 隐马尔可夫模型的基本概念

（1）补充马尔科夫概念：

马尔科夫假设：当前的状态只与之前的状态有关

马尔科夫过程：当前的状态只与前n个状态有关，被称为n阶马尔科夫模型。

马尔科夫链：可以理解为带有概率的状态转移链

一阶马尔科夫模型：当前的状态只与前一状态有关：

（a）若有M个状态，则共有M*M个状态转移

（b）转移概率：每一个状态转移都有一定的概率，称为~，所有的转移概率用一个M*M的矩阵表示

（c）每一个系统开始的时候，需要一个初始概率，称为π向量，表示每种状态作为初始状态出现的概率

隐马尔科夫模型：可能存在这样一种情况，我们想要的状态并不能直接观察得到，但是这个状态和其他某种可观测的状态之间存在一定的概率关系，也就是说可以通过那种可观测的状态（观测状态），来求解我们想要得到的状态（隐状态），这就是隐马尔科夫模型的主要思想。

（2）隐马尔可夫模型的定义

(a) 隐马尔可夫模型：隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列，称为状态序列(state sequence)：每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列(observation sequenoe )。序列的每一个位置又可以看作是一个时刻。

隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。隐马尔可夫模型的形式定义如下：

设Q是所有可能的状态的集合，V是所有可能的观测的集：

其中，N是可能的状态数，M是可能的观测数；

I是长度为T的状态序列，O是对应的观测序列：

A是状态转移概率矩阵：

其中，

表示：在时刻t处于状态qi的条件下在时刻t+1转移到状态qj的概率。

B是观测概率矩阵：

其中，

表示：在时刻t处于状态qj的条件下生成观测vk的概率。

π是初始状态概率向量：

其中，

表示：时刻t =1处于状态qi的概率。

(b)隐马尔可夫模型的三要素：

隐马尔可夫模型由初始状态概率向量π、状态转移概率矩阵A和观测概率矩阵B决定，其中，π个A决定状态序列，B决定观测序列。A，B，π称为隐马尔可夫模型的三要素，因此，隐马尔可夫模型λ可以用三元符号表示，即：。

状态转移概率矩阵A与初始状态概率向量π确定了隐藏的马尔可夫链，生成不可观测的状态序列。

观测概率矩阵B确定了如何从状态生成观测，与状态序列综合确定了如何产生观测序列。

(c)隐马尔可夫模型的两个基本假设：

假设一：齐次马尔可夫性假设，即假设隐藏的马尔可夫链在任意时刻t的状态只依赖于其前一时刻的状态，与其他时刻的状态及观测无关，也与时刻t无关，即：

假设二：观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测及状态无关：

隐马尔可夫模型可以用于标注，这时状态对应着标记。标注问题是给定观测的序列预测其对应的标记序列可以假设标注问题的数据是由隐马尔可夫模型生成的。这样我们可以利用隐马尔可夫模型的学习与预测算法进行标注。

有描述隐马尔可夫模型的例子如下：

解释：B的行列代表每个盒子得到红球或白球状态的概率。

（3）观测序列的生成过程

根据隐马尔可夫模型的定义，可将一个长度为T的观测序列的生成过程描述如下：

（4）隐马尔可夫模型的三个基本问题

(a)概率计算问题。给定模型和观测序列O=(o1,o2,... ,oT)，计算在模型λ下观测序列O出现的概率。

(b)学习问题。己知观测序列O=(o1,o2,... ,oT)，估计模型参数，使得在该模型下观测序列概率最大。即用极大似然估计的方法估计参数。

(c)预测问题，也称为解码(decoding)问题。己知模型和观测序列O=(o1,o2,... ,oT)，求对给定观测序列条件概率P(I | O)最大的状态序列I=(i1,i2,... ,iT)，即给定观测序列，求最有可能的对应的状态序列。

2. 概率计算算法

（1）直接计算（概念上可行实际不可行的方法）

给定模型和观测序列，需要计算观测序列O出现的概率。

最直接的想法是按照概率公式直接计算，通过列举所有可能的长度状态为T的序列I=(i1,i2,...,iT)，求各个状态序列I与观测序列O=(o1,o2,...,oT)的联合概率P(O,I|λ)，然后对所有可能的状态序列求和，得到,即：

状态序列I的概率是：

对固定的状态序列I，观测序列O的概率是：

O和I同时出现的联合概率为：

然后，对所有可能的状态序列I求和，得到观测序列O的概率：

但是，最后一个公式的计算量很大，是 $O(TN^T)$ 阶的，因此直接计算不可行。

（2）前向算法

前向概率：给定隐马尔可夫模型λ，定义到时刻t部分观测序列为o1,o2,...,ot，且状态为qi的概率为前向概率，记作：

可以递推地求得前项概率及观测序列概率。

观测序列概率的前向算法：

步骤(1)初始化前向概率，是初始时刻的状态i1=qi和观测o1的联合概率。

步骤(2)是前向概率的递推公式，计算到时刻t+1部分观测序列为o1,o2,... ,ot ,ot+1且在时刻t+1处于状态qi的前向概率，如图10.1所示。

αi(j)是到时刻t观测到o1,o2,... ,ot并在时刻t处于状态qj的前向概率，那么乘积αi(j)*αji就是到时刻t观测到o1,o2,... ,ot在在时刻t处于状态qj而在时刻t+1到达状态qi的联合概率。对这个乘积在时刻t的所有可能的N个状态qj求和，其结果就是到时刻t观测为o1,o2,... ,ot并在时刻t+1处于状态qi的联合概率。方括弧里的值与观测概率bi(ot+1)的乘积恰好是到时刻t+1观测到

o1,o2,... ,ot ,ot+1且在时刻t+1处于状态qi的前向概率。

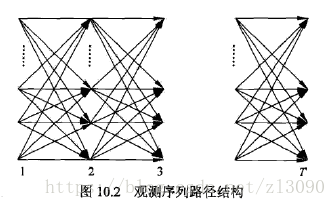
算法高效性的分析：高效的关键是其局部计算前向概率，然后利用路径结构（如下图所示）将前向概率递推到全局。具体地，在时刻t=1，计算α1(i)的N个值；在时刻t = 1,2,...,T-1，计算 $\alpha _{i+1}(i)$ 的N个值，而且每个时刻的 $\alpha _{i+1}(i)$ 的计算利用前一时刻N个 $\alpha _{i}(j)$ ，这样计算量减少的原因在于每一次直接引用前一次的计算结果，避免重复计算，计算量是 $O(N^2T)$ 阶。

看下面例子的计算来帮助理解计算过程：

（3）后向算法

后向概率：给定隐马尔可夫模型λ，定义在时刻t状态为qi的条件下，从t+1到T的部分观测序列为的概率为后向概率，记作：。

可以用递推的方法求得后向概率及观测序列概率，算法描述：

步骤(1)初始化初始化后向概率，对最终时刻的所有状态qi规定。

步骤(2)是后向概率的递推公式，如图10.3所示，为了计算在时刻t部状态为qi的条件下，从t+1到T的部分观测序列为ot+1,ot+2 ,... ,oT的后向概率。只需考虑在时刻t十1所有可能的N个状态qj的转移概率(即aij项)，以及在此状态下的观测ot+1的观测概率(即bj(oi+1)项)，然后考虑状态qj之后的观测序列的后向概率(即项)。

步骤(3)求解的思路与步骤(2)一致，只是初始概率代替转移概率。

后向概率递推公式的图解如下，它和前项的关系是可以看做图10.2的从一个点出发往前看（由它前面的计算得到它，也就是前像计算），以及从这个点出发往后看（由后边的计算得到它，后向计算）。

利用前向概率和后向概率的定义可以吧观测序列概率P(O|λ)统一写成：

当t=1或者t=T-1时，分别为式(10.17)和(10.21)

（4）一些概率与期望值的计算

（a）给定模型λ和观测O，在时刻t处于状态qi的概率，记为:

可以通过前向后向概率计算：

由前向概率和后向概率可知：

于是：

（b）给定模型λ和观测O，在时刻t处于状态qi且在t+1时刻处于状态qj的概率，记为：

可以通过前向后向概率计算：

而：

因此：

（c）将和对各个时刻t求和，可以得到一些有用的期望值：

在观测O下状态i出现的期望值：

在观测O下由状态i转移的期望值：

在观测O下由状态i转移到状态j的期望值：

3. 学习算法

隐马尔可夫模型的学习，根据训练数据是包括观测序列和对应的状态序列还是只有观测序列，可以分别由监督学习与非监督学习实现。

（1）监督学习方法

假设已给训练数据包含S个长度相同的观测序列和对应的状态序列｛(O1,I1),...,(Os,Is)｝，利用极大似然估计法来估计隐马尔可夫模型的参数。

（a）转移概率aij的估计
设样本中时t处于状态i时刻t+1转移到状态j的频数为Aij，那么状态转移概率的估计是

（b）观测概率bj(k)的估计

设样本中状态为j并观测为k的频数是Bjk，那么状态为j观测为k的概率的估计是

（c）初始状态概率的估计为S个样本中初始状态为qi的频率

（2）Baum-Welch算法

假设给定训练数据只包含S个长度为T的观测序列｛O1,...,Os)｝而没有对应的状态序列，目标是学习隐马尔可夫模型的参数。将观测序列数据看作观测数据O，状态序列数据看作不可观测的隐数据I，那么隐马尔可夫模型事实上是一个含有隐变量的概率模型：

它的参数学习可以由EM算法实现：

（a）确定完全数据的对数似然函数：

完全数据由观测数据和隐数据组成（O，I）=(o1,o2,... ,oT,i1,i2,... ,iT)，对数似然函数是

（b）EM算法的E步：求Q函数

其中 $\overline{\lambda }$ 是隐马尔可夫模型的当前估计值，λ是要极大化的隐马尔可夫模型参数：

于是：

（c）EM的M步：极大化Q函数求模型参数A,B,π

单独极大化上式(10.34)的每一项：

（3）Baum-Welch模型参数估计公式

将式(10.36)至(10.38)中的各概率分别用表示，可将相应的公式写成：

Baum-Welch算法：

4. 预测算法

（1）近似算法

近似算法的想法是：在每个时刻t选择在该时刻最有可能出现的状态 $i_{t}^{*}$ ，得到一个状态序列作为预测的结果。

在每一时刻t最有可能的状态 $i_{t}^{*}$ 通过下式得到：

近似算法的优点是计算简单，其缺点是不能保证预测的状态序列整体是最有可能的状态序列，因为预测的状态序列可能有实际不发生的部分。该方法得到的状态序列中有可能存在转移概率为0的相邻状态。

（2）维特比算法

维特比算法实际是用动态规划解隐马尔可夫模型预侧问题，即用动态规划(dynamic programming)求概率最大路径(最优路径)。一条路径对应着一个状态序列。

根据动态规划原理，最优路径具有这样的特性：如果最优路径在时刻t通过结点 $i_{t}^{*}$ ，那么这一路径从结点 $i_{t}^{*}$ 到终点 $i_{T}^{*}$ 的部分路径，对于从 $i_{t}^{*}$ 到 $i_{T}^{*}$ 的所有可能的部分路径来说，必须是最优的。依据这一原理，我们只需从时刻t=1开始，递推地计算在时刻t状态为i的各条部分路径的最大概率，直至得到时刻t=T状态为i的各条路径的最大概率。时刻t=T的最大概率即为最优路径的概率P*。

最优路径的终结点 $i_{T}^{*}$ 也同时得到。之后，从终结点 $i_{T}^{*}$ 开始，由后向前逐步求得结点。

维特比算法描述：

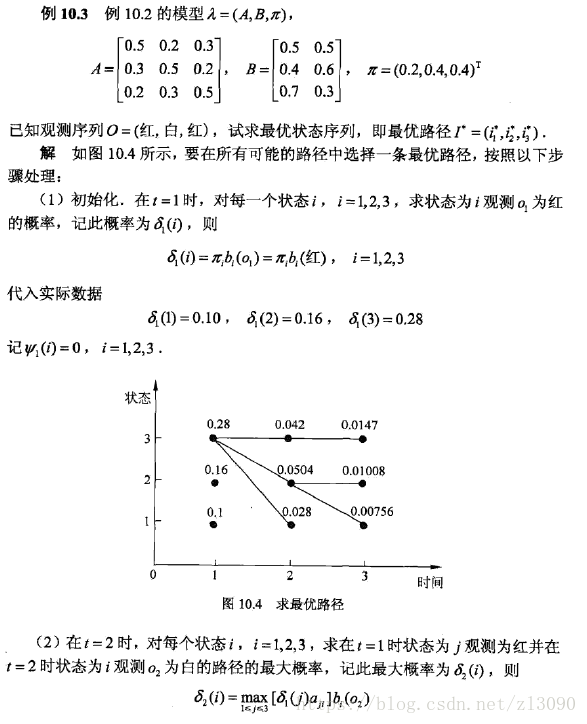
维特比算法的例子：

【统计学习方法-李航-笔记总结】十、隐马尔可夫模型

猜你喜欢