什么是独立同分布?
百度:
在概率统计理论中,指随机过程中,任何时刻的取值都为随机变量,如果这些随机变量服从同一分布,并且互相独立,那么这些随机变量是独立同分布。如果随机变量X1和X2独立,是指X1的取值不影响X2的取值,X2的取值也不影响X1的取值且随机变量X1和X2服从同一分布,这意味着X1和X2具有相同的分布形状和相同的分布参数,对离随机变量具有相同的分布律,对连续随机变量具有相同的概率密度函数,有着相同的分布函数,相同的期望、方差。如实验条件保持不变,一系列的抛硬币的正反面结果是独立同分布。
西瓜书:
输入空间中的所有样本服从一个隐含未知的分布,训练数据所有样本都是独立地从这个分布上采样而得。
为什么机器学习中, 要假设我们的数据是独立同分布的?
我们知道,机器学习就是利用当前获取到的信息(或数据)进行训练学习,用以对未来的数据进行预测、模拟。所以都是建立在历史数据之上,采用模型去拟合未来的数据。因此需要我们使用的历史数据具有总体的代表性。
为什么要有总体代表性?我们要从已有的数据(经验) 中总结出规律来对未知数据做决策,如果获取训练数据是不具有总体代表性的,就是特例的情况,那规律就会总结得不好或是错误,因为这些规律是由个例推算的,不具有推广的效果。
通过独立同分布的假设,就可以大大减小训练样本中个例的情形。
机器学习并不总是要求数据同分布。在不少问题中要求样本(数据)采样自同一个分布是因为希望用训练数据集训练得到的模型可以合理用于测试集,使用同分布假设能够使得这个做法解释得通。
由于现在的机器学习方向的内容已经变得比较广,存在不少机器学习问题并不要求样本同分布,比如一些发表在机器学习方向上的online算法就对数据分布没啥要求,关心的性质也非泛化性。
参考
链接:https://www.zhihu.com/question/41222495/answer/103066614
链接:https://www.zhihu.com/question/41222495/answer/103004055
什么是联合概率分布?
联合概率分布简称联合分布,是两个及以上随机变量组成的随机向量的概率分布。根据随机变量的不同,联合概率分布的表示形式也不同。对于离散型随机变量,联合概率分布可以以列表的形式表示,也可以以函数的形式表示;对于连续型随机变量,联合概率分布通过一非负函数的积分表示。
作者:tiankong_
来源:CSDN
原文:https://blog.csdn.net/tiankong_/article/details/78332666 !
欧氏距离(EUCLIDEAN DISTANCE)
欧氏距离定义: 欧氏距离( Euclidean distance)是一个通常采用的距离定义,它是在m维空间中两个点之间的真实距离。
在二维和三维空间中的欧式距离的就是两点之间的距离,二维的公式是
d = sqrt((x1-x2)^+(y1-y2)^)
三维的公式是
d=sqrt(x1-x2)^+(y1-y2)^+(z1-z2)^)
推广到n维空间,欧式距离的公式是
d=sqrt( ∑(xi1-xi2)^ ) 这里i=1,2..n
xi1表示第一个点的第i维坐标,xi2表示第二个点的第i维坐标
n维欧氏空间是一个点集,它的每个点可以表示为(x(1),x(2),...x(n)),其中x(i)(i=1,2...n)是实数,称为x的第i个坐标,两个点x和y=(y(1),y(2)...y(n))之间的距离d(x,y)定义为上面的公式.
欧氏距离看作信号的相似程度。 距离越近就越相似,就越容易相互干扰,误码率就越高。
目前该距离也会用于Web2.0的数据相似程度的分析,例如:用户喜好的相似程度。不过笔者不知道为什么是两变量的差值平方和?得好好再研究研究
====补充====
网上google一下,终于明白了,看下图,解释太明显了
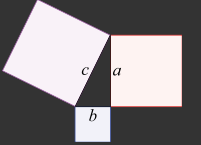
其实就是我们学的最简单的公式:a2+b2=c2,因此,两点距离其实就是:sqrt((x1-x2)^+(y1-y2)^)
监督学习与无监督学习
机器学习的常用方法,主要分为有监督学习(supervised learning)和无监督学习(unsupervised learning)。监督学习,就是人们常说的分类,通过已有的训练样本(即已知数据以及其对应的输出)去训练得到一个最优模型(这个模型属于某个函数的集合,最优则表示在某个评价准则下是最佳的),再利用这个模型将所有的输入映射为相应的输出,对输出进行简单的判断从而实现分类的目的,也就具有了对未知数据进行分类的能力。在人对事物的认识中,我们从孩子开始就被大人们教授这是鸟啊、那是猪啊、那是房子啊,等等。我们所见到的景物就是输入数据,而大人们对这些景物的判断结果(是房子还是鸟啊)就是相应的输出。当我们见识多了以后,脑子里就慢慢地得到了一些泛化的模型,这就是训练得到的那个(或者那些)函数,从而不需要大人在旁边指点的时候,我们也能分辨的出来哪些是房子,哪些是鸟。监督学习里典型的例子就是KNN、SVM。无监督学习(也有人叫非监督学习,反正都差不多)则是另一种研究的比较多的学习方法,它与监督学习的不同之处,在于我们事先没有任何训练样本,而需要直接对数据进行建模。这听起来似乎有点不可思议,但是在我们自身认识世界的过程中很多处都用到了无监督学习。比如我们去参观一个画展,我们完全对艺术一无所知,但是欣赏完多幅作品之后,我们也能把它们分成不同的派别(比如哪些更朦胧一点,哪些更写实一些,即使我们不知道什么叫做朦胧派,什么叫做写实派,但是至少我们能把他们分为两个类)。无监督学习里典型的例子就是聚类了。聚类的目的在于把相似的东西聚在一起,而我们并不关心这一类是什么。因此,一个聚类算法通常只需要知道如何计算相似度就可以开始工作了。
那么,什么时候应该采用监督学习,什么时候应该采用非监督学习呢?我也是从一次面试的过程中被问到这个问题以后才开始认真地考虑答案。一种非常简单的回答就是从定义入手,如果我们在分类的过程中有训练样本(training data),则可以考虑用监督学习的方法;如果没有训练样本,则不可能用监督学习的方法。但是事实上,我们在针对一个现实问题进行解答的过程中,即使我们没有现成的训练样本,我们也能够凭借自己的双眼,从待分类的数据中人工标注一些样本,并把他们作为训练样本,这样的话就可以把条件改善,用监督学习的方法来做。当然不得不说的是有时候数据表达的会非常隐蔽,也就是说我们手头的信息不是抽象的形式,而是具体的一大堆数字,这样我们很难凭借人本身对它们简单地进行分类。这个说的好像有点不大明白,举个例子说就是在bag-of-words模型的时候,我们利用k-means的方法聚类从而对数据投影,这时候用k-means就是因为我们当前到手的只有一大堆数据,而且是很高维的,当我们想把他们分为50个类的时候,我们已经无力将每个数据标记说这个数应该是哪个类,那个数又应该是哪个类了。所以说遇到这种情况也只有无监督学习能够帮助我们了。那么这么说来,能不能再深入地问下去,如果有训练样本(或者说如果我们可以获得到一些训练数据的话),监督学习就会比无监督学习更合适呢?(照我们单纯地想,有高人教总比自己领悟来的准,来的快吧!)我觉得一般来说,是这样的,但是这要具体看看训练数据的获取。本人在最近课题的研究中,手动标注了大量的训练样本(当然这些样本基本准确了),而且把样本画在特征空间中发现线性可分性非常好,只是在分类面附近总有一些混淆的数据样本,从而用线性分类器进行分类之后这样样本会被误判。然而,如果用混合高斯模型(GMM)来分的话,这些易混淆的点被正确分类的更多了。对这个现象的一个解释,就是不管是训练样本,还是待聚类的数据,并不是所有数据都是相互独立同分布的。换句话说,数据与数据的分布之间存在联系。在我阅读监督学习的大量材料中,大家都没有对训练数据的这一假设(独立同分布)进行说明,直到我阅读到一本书的提示后才恍然大悟。对于不同的场景,正负样本的分布如果会存在偏移(可能是大的偏移,也可能偏移比较小),这样的话用监督学习的效果可能就不如用非监督学习了。
---------------------
作者:姜文晖
来源:CSDN
原文:https://blog.csdn.net/jwh_bupt/article/details/7654120
深入浅出--梯度下降法及其实现
- 梯度下降的场景假设
- 梯度
- 梯度下降算法的数学解释
- 梯度下降算法的实例
- 梯度下降算法的实现
- Further reading
本文将从一个下山的场景开始,先提出梯度下降算法的基本思想,进而从数学上解释梯度下降算法的原理,最后实现一个简单的梯度下降算法的实例!
梯度下降的场景假设
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
 image.png
image.png
我们同时可以假设这座山最陡峭的地方是无法通过肉眼立马观察出来的,而是需要一个复杂的工具来测量,同时,这个人此时正好拥有测量出最陡峭方向的能力。所以,此人每走一段距离,都需要一段时间来测量所在位置最陡峭的方向,这是比较耗时的。那么为了在太阳下山之前到达山底,就要尽可能的减少测量方向的次数。这是一个两难的选择,如果测量的频繁,可以保证下山的方向是绝对正确的,但又非常耗时,如果测量的过少,又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率,来确保下山的方向不错误,同时又不至于耗时太多!
梯度下降
梯度下降的基本过程就和下山的场景很类似。
首先,我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值,也就是山底。根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向(在后面会详细解释)
所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段。那么为什么梯度的方向就是最陡峭的方向呢?接下来,我们从微分开始讲起
微分
看待微分的意义,可以有不同的角度,最常用的两种是:
- 函数图像中,某点的切线的斜率
-
函数的变化率
几个微分的例子:
 image.png
image.png
上面的例子都是单变量的微分,当一个函数有多个变量的时候,就有了多变量的微分,即分别对每个变量进行求微分

梯度
梯度实际上就是多变量微分的一般化。
下面这个例子:

我们可以看到,梯度就是分别对每个变量进行微分,然后用逗号分割开,梯度是用<>包括起来,说明梯度其实一个向量。
梯度是微积分中一个很重要的概念,之前提到过梯度的意义
- 在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率
- 在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向
这也就说明了为什么我们需要千方百计的求取梯度!我们需要到达山底,就需要在每一步观测到此时最陡峭的地方,梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。所以我们只要沿着梯度的方向一直走,就能走到局部的最低点!

梯度下降算法的数学解释
上面我们花了大量的篇幅介绍梯度下降算法的基本思想和场景假设,以及梯度的概念和思想。下面我们就开始从数学上解释梯度下降算法的计算过程和思想!

此公式的意义是:J是关于Θ的一个函数,我们当前所处的位置为Θ0点,要从这个点走到J的最小值点,也就是山底。首先我们先确定前进的方向,也就是梯度的反向,然后走一段距离的步长,也就是α,走完这个段步长,就到达了Θ1这个点!

下面就这个公式的几个常见的疑问:
- α是什么含义?
α在梯度下降算法中被称作为学习率或者步长,意味着我们可以通过α来控制每一步走的距离,以保证不要步子跨的太大扯着蛋,哈哈,其实就是不要走太快,错过了最低点。同时也要保证不要走的太慢,导致太阳下山了,还没有走到山下。所以α的选择在梯度下降法中往往是很重要的!α不能太大也不能太小,太小的话,可能导致迟迟走不到最低点,太大的话,会导致错过最低点!

- 为什么要梯度要乘以一个负号?
梯度前加一个负号,就意味着朝着梯度相反的方向前进!我们在前文提到,梯度的方向实际就是函数在此点上升最快的方向!而我们需要朝着下降最快的方向走,自然就是负的梯度的方向,所以此处需要加上负号
梯度下降算法的实例
我们已经基本了解了梯度下降算法的计算过程,那么我们就来看几个梯度下降算法的小实例,首先从单变量的函数开始
单变量函数的梯度下降
我们假设有一个单变量的函数

函数的微分

初始化,起点为

学习率为

根据梯度下降的计算公式

我们开始进行梯度下降的迭代计算过程:

如图,经过四次的运算,也就是走了四步,基本就抵达了函数的最低点,也就是山底

多变量函数的梯度下降
我们假设有一个目标函数

现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0,0)点。但是接下来,我们会从梯度下降算法开始一步步计算到这个最小值!
我们假设初始的起点为:

初始的学习率为:

函数的梯度为:

进行多次迭代:

我们发现,已经基本靠近函数的最小值点

梯度下降算法的实现
下面我们将用python实现一个简单的梯度下降算法。场景是一个简单的线性回归的例子:假设现在我们有一系列的点,如下图所示

我们将用梯度下降法来拟合出这条直线!
首先,我们需要定义一个代价函数,在此我们选用均方误差代价函数

此公示中
- m是数据集中点的个数
- ½是一个常量,这样是为了在求梯度的时候,二次方乘下来就和这里的½抵消了,自然就没有多余的常数系数,方便后续的计算,同时对结果不会有影响
- y 是数据集中每个点的真实y坐标的值
-
h 是我们的预测函数,根据每一个输入x,根据Θ 计算得到预测的y值,即
 image.png
image.png
我们可以根据代价函数看到,代价函数中的变量有两个,所以是一个多变量的梯度下降问题,求解出代价函数的梯度,也就是分别对两个变量进行微分

明确了代价函数和梯度,以及预测的函数形式。我们就可以开始编写代码了。但在这之前,需要说明一点,就是为了方便代码的编写,我们会将所有的公式都转换为矩阵的形式,python中计算矩阵是非常方便的,同时代码也会变得非常的简洁。
为了转换为矩阵的计算,我们观察到预测函数的形式

我们有两个变量,为了对这个公式进行矩阵化,我们可以给每一个点x增加一维,这一维的值固定为1,这一维将会乘到Θ0上。这样就方便我们统一矩阵化的计算

然后我们将代价函数和梯度转化为矩阵向量相乘的形式

coding time
首先,我们需要定义数据集和学习率
1 import numpy as np 2 3 # Size of the points dataset. 4 m = 20 5 6 # Points x-coordinate and dummy value (x0, x1). 7 X0 = np.ones((m, 1)) 8 X1 = np.arange(1, m+1).reshape(m, 1) 9 X = np.hstack((X0, X1)) 10 11 # Points y-coordinate 12 y = np.array([ 13 3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12, 14 11, 13, 13, 16, 17, 18, 17, 19, 21 15 ]).reshape(m, 1) 16 17 # The Learning Rate alpha. 18 alpha = 0.01
接下来我们以矩阵向量的形式定义代价函数和代价函数的梯度
1 def error_function(theta, X, y): 2 '''Error function J definition.''' 3 diff = np.dot(X, theta) - y 4 return (1./2*m) * np.dot(np.transpose(diff), diff) 5 6 def gradient_function(theta, X, y): 7 '''Gradient of the function J definition.''' 8 diff = np.dot(X, theta) - y 9 return (1./m) * np.dot(np.transpose(X), diff)
最后就是算法的核心部分,梯度下降迭代计算
1 def gradient_descent(X, y, alpha): 2 '''Perform gradient descent.''' 3 theta = np.array([1, 1]).reshape(2, 1) 4 gradient = gradient_function(theta, X, y) 5 while not np.all(np.absolute(gradient) <= 1e-5): 6 theta = theta - alpha * gradient 7 gradient = gradient_function(theta, X, y) 8 return theta
当梯度小于1e-5时,说明已经进入了比较平滑的状态,类似于山谷的状态,这时候再继续迭代效果也不大了,所以这个时候可以退出循环!
完整的代码如下
1 import numpy as np 2 3 # Size of the points dataset. 4 m = 20 5 6 # Points x-coordinate and dummy value (x0, x1). 7 X0 = np.ones((m, 1)) 8 X1 = np.arange(1, m+1).reshape(m, 1) 9 X = np.hstack((X0, X1)) 10 11 # Points y-coordinate 12 y = np.array([ 13 3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12, 14 11, 13, 13, 16, 17, 18, 17, 19, 21 15 ]).reshape(m, 1) 16 17 # The Learning Rate alpha. 18 alpha = 0.01 19 20 def error_function(theta, X, y): 21 '''Error function J definition.''' 22 diff = np.dot(X, theta) - y 23 return (1./2*m) * np.dot(np.transpose(diff), diff) 24 25 def gradient_function(theta, X, y): 26 '''Gradient of the function J definition.''' 27 diff = np.dot(X, theta) - y 28 return (1./m) * np.dot(np.transpose(X), diff) 29 30 def gradient_descent(X, y, alpha): 31 '''Perform gradient descent.''' 32 theta = np.array([1, 1]).reshape(2, 1) 33 gradient = gradient_function(theta, X, y) 34 while not np.all(np.absolute(gradient) <= 1e-5): 35 theta = theta - alpha * gradient 36 gradient = gradient_function(theta, X, y) 37 return theta 38 39 optimal = gradient_descent(X, y, alpha) 40 print('optimal:', optimal) 41 print('error function:', error_function(optimal, X, y)[0,0])
运行代码,计算得到的结果如下

所拟合出的直线如下

小结
至此,我们就基本介绍完了梯度下降法的基本思想和算法流程,并且用python实现了一个简单的梯度下降算法拟合直线的案例!
最后,我们回到文章开头所提出的场景假设:
这个下山的人实际上就代表了反向传播算法,下山的路径其实就代表着算法中一直在寻找的参数Θ,山上当前点的最陡峭的方向实际上就是代价函数在这一点的梯度方向,场景中观测最陡峭方向所用的工具就是微分 。在下一次观测之前的时间就是有我们算法中的学习率α所定义的。
可以看到场景假设和梯度下降算法很好的完成了对应!
Further reading
作者:六尺帐篷
链接:https://www.jianshu.com/p/c7e642877b0e
來源:简书
逻辑回归通过拟合曲线(或者学习超平面)实现分类,决策树通过寻找最佳划分特征进而学习样本路径实现分类,支持向量机通过寻找分类超平面进而最大化类别间隔实现分类。相比之下,朴素贝叶斯独辟蹊径,通过考虑特征概率来预测分类。
参考:https://blog.csdn.net/li8zi8fa/article/details/76176597

