一.基本概念
1、顶点(vertex)
表示某个事物或对象。由于图的术语没有标准化,因此,称顶点为点、节点、结点、端点等都是可以的。
2、边(edge)
通俗点理解就是两个点相连组合成一条边,表示事物与事物之间的关系。需要注意的是边表示的是顶点之间的逻辑关系,粗细长短都无所谓的。包括上面的顶点也一样,表示逻辑事物或对象,画的时候大小形状都无所谓。
3、同构(Isomorphism )
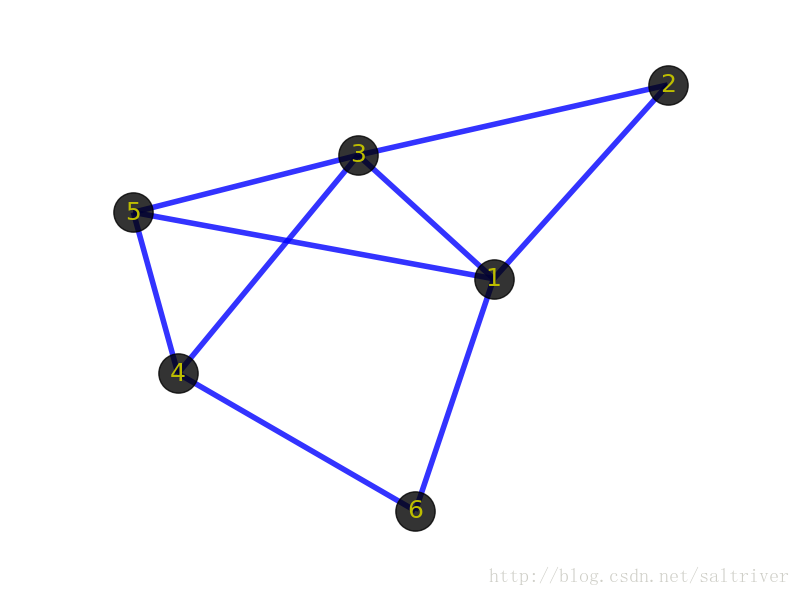
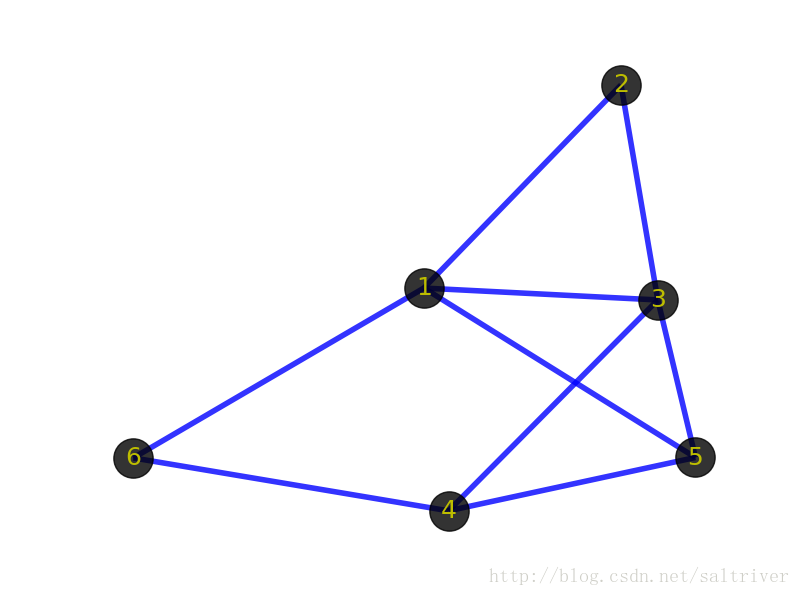
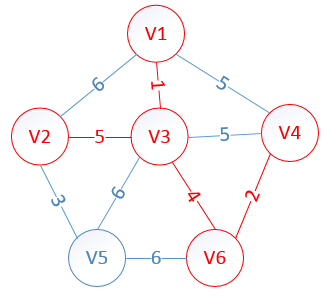
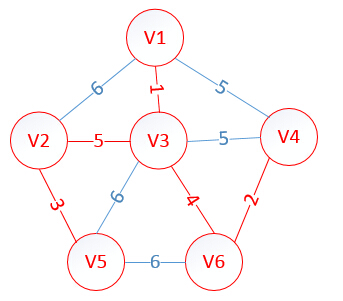
先看看下面2张图:
首先你的感觉是这2个图肯定不一样。但从图(graph)的角度出发,这2个图是一样的,即它们是同构的。前面提到顶点和边指的是事物和事物的逻辑关系,不管顶点的位置在哪,边的粗细长短如何,只要不改变顶点代表的事物本身,不改变顶点之间的逻辑关系,那么就代表这些图拥有相同的信息,是同一个图。同构的图区别仅在于画法不同。
4、有向/无向图(Directed Graph/ Undirected Graph)
最基本的图通常被定义为“无向图”,与之对应的则被称为“有向图”。两者唯一的区别在于,有向图中的边是有方向性的。有向图和无向图的许多原理和算法是相通的。
5、权重(weight)
边的权重(或者称为权值、开销、长度等),也是一个非常核心的概念,即每条边都有与之对应的值。例如当顶点代表某些物理地点时,两个顶点间边的权重可以设置为路网中的开车距离。有时候为了应对特殊情况,边的权重可以是零或者负数,也别忘了“图”是用来记录关联的东西,并不是真正的地图。
6、路径/最短路径(path/shortest path)
在图上任取两顶点,分别作为起点(start vertex)和终点(end vertex),我们可以规划许多条由起点到终点的路线。不会来来回回绕圈子、不会重复经过同一个点和同一条边的路线,就是一条“路径”。两点之间存在路径,则称这2个顶点是连通的(connected)。
还是上图的例子,北京->上海->广州,是一条路径,北京->武汉->广州,是另一条路径,北京—>武汉->上海->广州,也是一条路径。而北京->武汉->广州这条路径最短,称为最短路径。
路径也有权重。路径经过的每一条边,沿路加权重,权重总和就是路径的权重(通常只加边的权重,而不考虑顶点的权重)。在路网中,路径的权重,可以想象成路径的总长度。在有向图中,路径还必须跟随边的方向。
值得注意的是,一条路径包含了顶点和边,因此路径本身也构成了图结构,只不过是一种特殊的图结构。
7、环(loop)
环,也成为环路,是一个与路径相似的概念。在路径的终点添加一条指向起点的边,就构成一条环路。通俗点说就是绕圈。与路径一样,有向图中的环路也必须跟随边的方向。环本身也是一种特殊的图结构。
8、连通图/连通分量(connected graph/connected component)
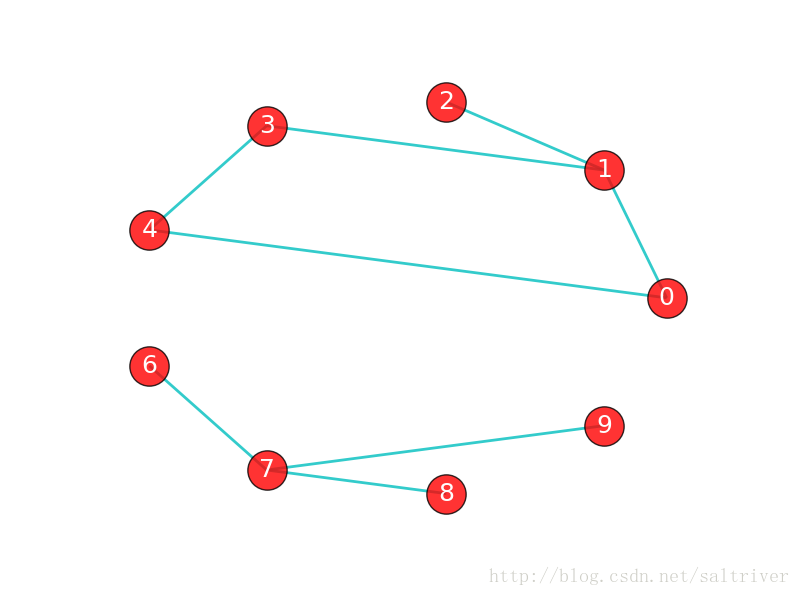
如果在图G中,任意2个顶点之间都存在路径,那么称G为连通图(注意是任意2顶点)。上面那张城市之间的图,每个城市之间都有路径,因此是连通图。而下面这张图中,顶点8和顶点2之间就不存在路径,因此下图不是一个连通图,当然该图中还有很多顶点之间不存在路径。
上图虽然不是一个连通图,但它有多个连通子图:0,1,2顶点构成一个连通子图,0,1,2,3,4顶点构成的子图是连通图,6,7,8,9顶点构成的子图也是连通图,当然还有很多子图。我们把一个图的最大连通子图称为它的连通分量。0,1,2,3,4顶点构成的子图就是该图的最大连通子图,也就是连通分量。连通分量有如下特点:
1)是子图;
2)子图是连通的;
3)子图含有最大顶点数。
注意:“最大连通子图”指的是无法再扩展了,不能包含更多顶点和边的子图。0,1,2,3,4顶点构成的子图已经无法再扩展了。
显然,对于连通图来说,它的最大连通子图就是其本身,连通分量也是其本身。
二.图的两种表示形式
1、邻接表
邻接表的核心思想就是针对每个顶点设置一个邻居表。
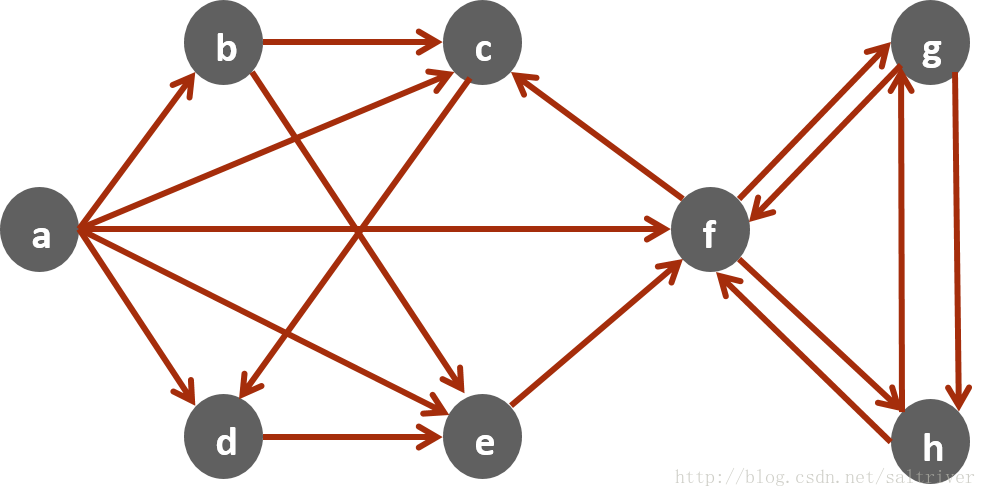
以上面的图为例,这是一个有向图,分别有顶点a, b, c, d, e, f, g, h共8个顶点。使用邻接表就是针对这8个顶点分别构建邻居表,从而构成一个8个邻居表组成的结构,这个结构就是我们这个图的表示结构或者叫存储结构。
a, b, c, d, e, f, g, h = range(8)
N = [{b, c, d, e, f}, # a 的邻居表
{c, e}, # b 的邻居表
{d}, # c 的邻居表
{e}, # d 的邻居表
{f}, # e 的邻居表
{c, g, h}, # f 的邻居表
{f, h}, # g 的邻居表
{f, g}] # h 的邻居表个人觉得在java里面用map存储比较好,key用来存储定点,value用来存储与顶点相关的其他顶点集合。
2、邻接矩阵
(2)邻接矩阵
邻接矩阵的核心思想是针对每个顶点设置一个表,这个表包含所有顶点,通过True/False来表示是否是邻居顶点。
还是针对上面的图,分别有顶点a, b, c, d, e, f, g, h共8个顶点。使用邻接矩阵就是针对这8个顶点构建一个8×8的矩阵组成的结构,这个结构就是我们这个图的表示结构或存储结构。
在邻接矩阵表示法中,有一些非常实用的特性。
- 首先,可以看出,该矩阵是一个方阵,方阵的维度就是图中顶点的数量,同时还是一个对称矩阵,这样进行处理时非常方便。
- 其次,该矩阵对角线表示的是顶点与顶点自身的关系,一般图不允许出现自关联状态,即自己指向自己的边,那么对角线的元素全部为0;
- 最后,该表示方式可以不用改动即可表示带权值的图,直接将原来存储1的地方修改成相应的权值即可。当然, 0也是权值的一种,而邻接矩阵中0表示不存在这条边。出于实践中的考虑,可以对不存在的边的权值进行修改,将其设置为无穷大或非法的权值,如None,-99999/99999等
三.广度优先搜索(BFS)
BFS使用队列(queue)来实施算法过程,队列(queue)有着先进先出FIFO(First Input First Output)的特性,BFS操作步骤如下:
1、把起始点放入queue;
2、重复下述2步骤,直到queue为空为止:
1) 从queue中取出队列头的点;
2) 找出与此点邻接的且尚未遍历的点,进行标记,然后全部放入queue中
具体流程图可参考:https://blog.csdn.net/saltriver/article/details/54428983
四.深度优先搜索(DFS)
DFS的实现方式相比于BFS应该说大同小异,只是把queue换成了stack而已,stack具有后进先出LIFO(Last Input First Output)的特性,DFS的操作步骤如下:
1、把起始点放入stack;
2、重复下述3步骤,直到stack为空为止:
- 从stack中访问栈顶的点;
- 找出与此点邻接的且尚未遍历的点,进行标记,然后全部放入stack中;
- 如果此点没有尚未遍历的邻接点,则将此点从stack中弹出。
具体流程图可参考:https://blog.csdn.net/saltriver/article/details/54429068
五.最小生成树
1.Prim算法
MST(Minimum Spanning Tree,最小生成树)问题有两种通用的解法,Prim算法就是其中之一,它是从点的方面考虑构建一颗MST,大致思想是:设图G顶点集合为U,首先任意选择图G中的一点作为起始点a,将该点加入集合V,再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小,此时将b点也加入集合V;以此类推,现在的集合V={a,b},再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小,此时将c点加入集合V,直至所有顶点全部被加入V,此时就构建出了一颗MST。因为有N个顶点,所以该MST就有N-1条边,每一次向集合V中加入一个点,就意味着找到一条MST的边。
用图示和代码说明:
初始状态:
设置2个数据结构:
lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST
mst[i]:表示对应lowcost[i]的起点,即说明边<mst[i],i>是MST的一条边,当mst[i]=0表示起点i加入MST
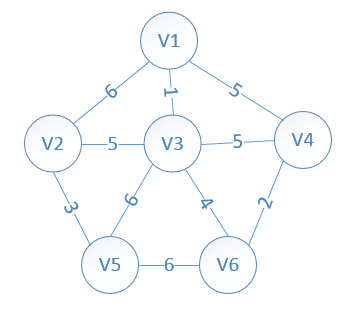
我们假设V1是起始点,进行初始化(*代表无限大,即无通路):
lowcost[2]=6,lowcost[3]=1,lowcost[4]=5,lowcost[5]=*,lowcost[6]=*
mst[2]=1,mst[3]=1,mst[4]=1,mst[5]=1,mst[6]=1,(所有点默认起点是V1)
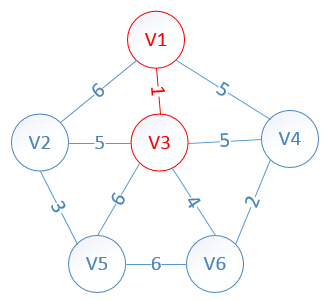
明显看出,以V3为终点的边的权值最小=1,所以边<mst[3],3>=1加入MST
此时,因为点V3的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=5,lowcost[5]=6,lowcost[6]=4
mst[2]=3,mst[3]=0,mst[4]=1,mst[5]=3,mst[6]=3
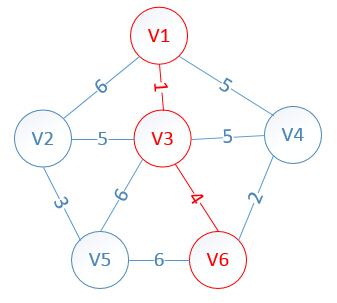
明显看出,以V6为终点的边的权值最小=4,所以边<mst[6],6>=4加入MST
此时,因为点V6的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=2,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=6,mst[5]=3,mst[6]=0
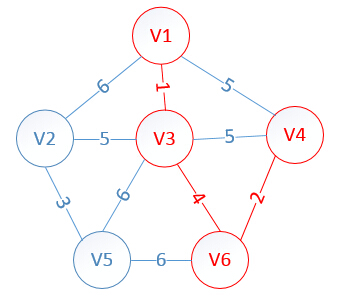
明显看出,以V4为终点的边的权值最小=2,所以边<mst[4],4>=4加入MST
此时,因为点V4的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=0,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=0,mst[5]=3,mst[6]=0
明显看出,以V2为终点的边的权值最小=5,所以边<mst[2],2>=5加入MST
此时,因为点V2的加入,需要更新lowcost数组和mst数组:
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=3,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=2,mst[6]=0
很明显,以V5为终点的边的权值最小=3,所以边<mst[5],5>=3加入MST
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=0,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=0,mst[6]=0
至此,MST构建成功,如图所示:
int graph[MAX][MAX];
int prim(int graph[][MAX], int n)
{
int lowcost[MAX];
int mst[MAX];
int i, j, min, minid, sum = 0;
//将与第一个点相连的边的长度都遍历到lowcost数组中
for (i = 2; i < n; i++)
{
lowcost[i] = graph[0][i];
mst[i] = 1;
}
mst[1] = 0;
for (i = 2; i < n; i++)
{
min = MAXCOST;
minid = 0;
//找出最小的一条边
for (j = 2; j < n; j++)
{
if (lowcost[j] < min && lowcost[j] != 0)
{
min = lowcost[j];
minid = j;
}
}
system.out.println("V"+mst[minid]+"-V"+minid+"="+min);
sum += min;
//将已经选中过的边置为0,下次筛选的时候会过滤
lowcost[minid] = 0;
//遍历一遍lowcost数组,倘若新加入终点的边与lowcost中相同终点的边的值更小,则替换
for (j = 2; j < n; j++)
{
if (graph[minid][j] < lowcost[j])
{
lowcost[j] = graph[minid][j];
mst[j] = minid;
}
}
}
return sum;
}转载:https://blog.csdn.net/yeruby/article/details/38615045
2.Kruskal算法
1、Kruskal算法描述
Kruskal算法是基于贪心的思想得到的。首先我们把所有的边按照权值先从小到大排列,接着按照顺序选取每条边,如果这条边的两个端点不属于同一集合,那么就将它们合并,直到所有的点都属于同一个集合为止。至于怎么合并到一个集合,那么这里我们就可以用到一个工具——-并查集(不知道的同学请移步:Here)。换而言之,Kruskal算法就是基于并查集的贪心算法。
2、Kruskal算法流程
对于图G(V,E),以下是算法描述:
-
输入: 图G -
输出: 图G的最小生成树 -
具体流程: -
(1)将图G看做一个森林,每个顶点为一棵独立的树 -
(2)将所有的边加入集合S,即一开始S = E -
(3)从S中拿出一条最短的边(u,v),如果(u,v)不在同一棵树内,则连接u,v合并这两棵树,同时将(u,v)加入生成树的边集E' -
(4)重复(3)直到所有点属于同一棵树,边集E'就是一棵最小生成树
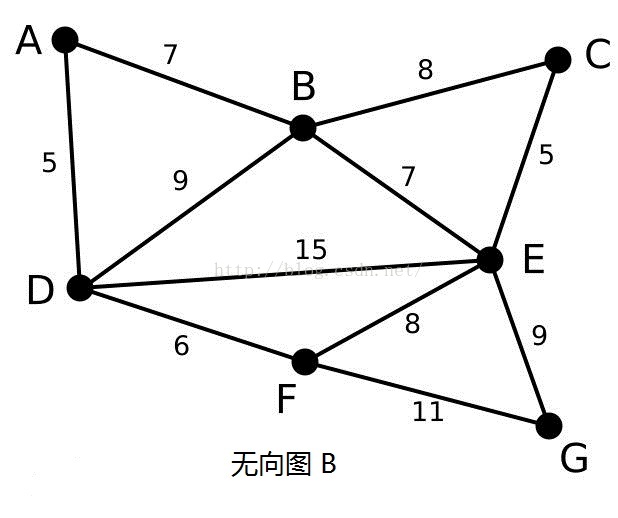
我们用现在来模拟一下Kruskal算法,下面给出一个无向图B,我们使用Kruskal来找无向图B的最小生成树。
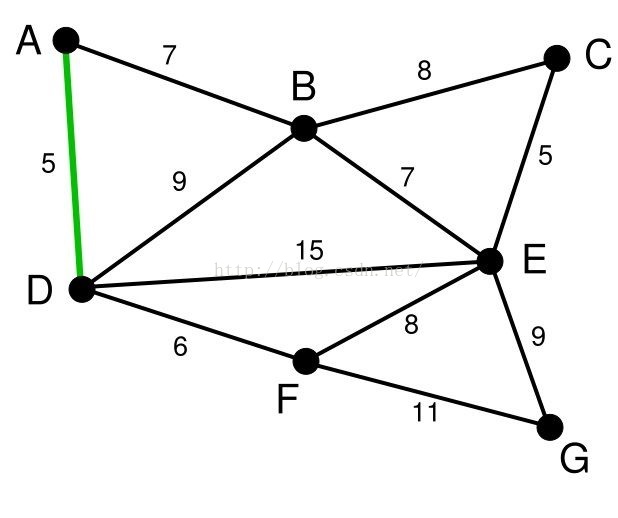
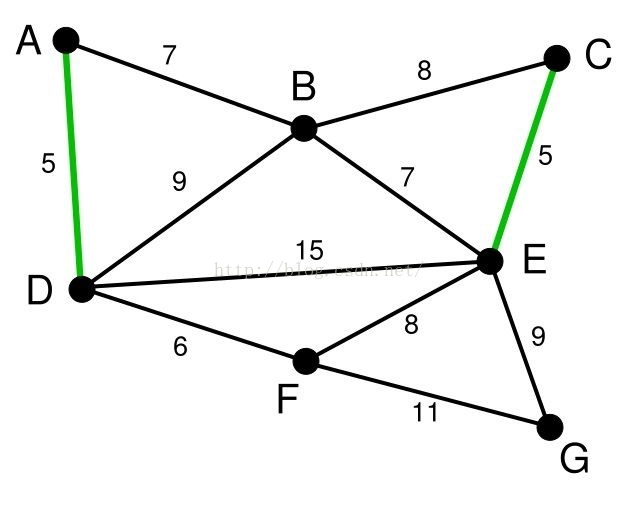
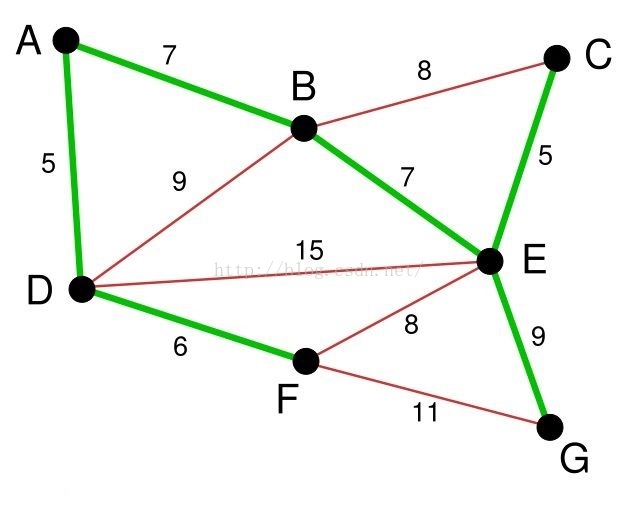
首先,我们将所有的边都进行从小到大的排序。排序之后根据贪心准则,我们选取最小边(A,D)。我们发现顶点A,D不在一棵树上,所以合并顶点A,D所在的树,并将边(A,D)加入边集E‘。
我们接着在剩下的边中查找权值最小的边,于是我们找到的(C,E)。我们可以发现,顶点C,E仍然不在一棵树上,所以我们合并顶点C,E所在的树,并将边(C,E)加入边集E'
不断重复上述的过程,于是我们就找到了无向图B的最小生成树,如下图所示:
3、Kruskal算法的时间复杂度
Kruskal算法每次要从都要从剩余的边中选取一个最小的边。通常我们要先对边按权值从小到大排序,这一步的时间复杂度为为O(|Elog|E|)。Kruskal算法的实现通常使用并查集,来快速判断两个顶点是否属于同一个集合。最坏的情况可能要枚举完所有的边,此时要循环|E|次,所以这一步的时间复杂度为O(|E|α(V)),其中α为Ackermann函数,其增长非常慢,我们可以视为常数。所以Kruskal算法的时间复杂度为O(|Elog|E|)。
作者代码的实现可以添加一个节点结束器,每联合一个节点就加一,当节点数达到图中的总节点数的时候,就break跳出循环;
//自己写的,代码为测试,有问题欢迎指出
class Kruskal{
int nodeNum;
List<Side> listSide;
public Kruskal(String[] node,int[][] graph){
nodeNum = node.length;
//去除重复,取二维数组的斜三角
for(int i=1;i<nodeNum;i++){
for(int j=0;j<i;j++){
if(graph[i][j]>0){
Side side = new Side();
side.start = i;
side.end = j;
side.length = graph[i][j];
listNode.add(side);
}
}
}
}
//定义边
class Side{
private int start;
private int end;
private int length;
}
public void init(){
this.father = new int[nodeNum];
for(int i=0;i<nodeNum;i++){
father[i] = -1;
}
}
public int find(int x){
if(father[X] <= 0)
return X;
else
return father[X] = find(father[X]);
}
public void union(int root1,int root2){
if (father[root2]<father[root1]){
father[root1] = root2;
}else{
if (father[root1]==father[root2])
father[root1] --;
father[root2] = root1;
}
}
public int printKruskal(){
//将边按长度从小到大排序
Sort(listSide);
int currentNodeNum = 1;
int sum = 0;
for(int i=0;i<listSide.size();i++){
int startNode = listSide.get(i).start;
int endNode = listSide.get(i).end;
//这里使用交并集解决会连城圈的问题
if(find(startNode) == -1 && find(endNode) == -1){
union(startNode,endNode);
nodeNum ++;
sum += listSide.get(i).length;
}else if(find(startNode) != find(endNode)){
union(startNode,endNode);
nodeNum ++;
sum += listSide.get(i).length;
}
if(currentNodeNum == nodeNum) break;
}
}
}转载:https://blog.csdn.net/luomingjun12315/article/details/47700237
6.最短路径
代码好理解:https://blog.csdn.net/qibofang/article/details/51594673
文字好理解:https://blog.csdn.net/tianjing0805/article/details/76023080