版权声明:本文为博主原创学习笔记,如需转载请注明来源。 https://blog.csdn.net/SHU15121856/article/details/84197607
学习《Python与机器学习实战》和《scikit-learn机器学习》时的一些实践。
随机漫步
import matplotlib.pyplot as plt
import numpy as np
'''
一维随机漫步
'''
# 博弈组数
n_person = 2000
# 每组抛硬币次数
n_times = 500
# 抛硬币次数序列,用于当绘制点的横坐标
t = np.arange(n_times)
# 一共n_person组,每组是n_times个-1或者1这两个数组成的序列表示输和赢
# 即相当于创建0~1的整数(只有0和1),再*2-1也就是只有-1和1这两个数字组成的了
steps = 2 * np.random.random_integers(0, 1, (n_person, n_times)) - 1
# np.cumsum返回给定axis上的累计和
# 这里就是将二维steps的所有列逐步加起来的中间结果
# 这也是一个二维数组,反映了每组在博弈过程中逐步变化的的输赢总额
amounts = np.cumsum(steps, axis=1)
# 每个元素平方
sd_amount = amounts ** 2
# 再求所有行(组)的平均值
mean_sd_amount = sd_amount.mean(axis=0)
# Latex
plt.xlabel(r"$t$")
plt.ylabel(r"$\sqrt {\langle (\delta x)^2 \rangle}$")
# 绘制两条曲线
plt.plot(t, np.sqrt(mean_sd_amount), 'g.', t, np.sqrt(t), 'r-')
plt.show()
运行结果:

埃拉托色尼筛法
import numpy as np
'''
Sieve of Eratosthenes打印1~100中的质数
'''
# 生成从1~100的数组
a = np.arange(1, 101)
# 该方法最多到开方位置即完成
n_max = int(np.sqrt(len(a)))
# 初始化所有数都设置为"是质数"
is_prime = np.ones(len(a), dtype=bool)
# 1不是质数,2是质数,已经默认设置成True
is_prime[0] = False
for i in range(2, n_max):
# 如果i是质数
if i in a[is_prime]:
# 从i^2开始每次+i的数都因为能被i整除所以不是质数
is_prime[(i ** 2 - 1)::i] = False
# 这里使用从i^2开始,那么比i小的i的倍数都在前面的迭代中设置过为False了
print(a[is_prime])
运行结果:
[ 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89
97]
蒙特卡洛算法求
import numpy as np
'''
蒙特卡洛算法求π
'''
# 圆的半径设置为1,生成100W个点
n_dotes = 1000000
# random.random()生成0和1之间的随机浮点数
x = np.random.random(n_dotes)
y = np.random.random(n_dotes)
# 计算到圆心(原点)的距离.这里不对欧氏距离开方,后面只要用半径r^2=1比较就行
distance = x ** 2 + y ** 2
# 判断是否在圆内,使用布尔索引
in_circle = distance[distance < 1]
pi = 4 * float(len(in_circle)) / n_dotes
print(pi)
运行结果:3.143448
多项式回归
import numpy as np
import matplotlib.pyplot as plt
# 使matplotlib正常显示负号
plt.rcParams['axes.unicode_minus'] = False
BASE_DIR = "E:/WorkSpace/ReadingNotes/Python与机器学习实战"
# 训练样本,利用样本xs->ys来计算n次多项式系数ps
# 即获取使得MSE损失即[f(x,p)-y]^2最小的n次多项式系数p的序列
def train(xs, ys, n):
ps = np.polyfit(xs, ys, n)
assert len(ps) == n + 1 # 多项式系数从p0~pn,其数目一定是n+1
return ps
# 以训练结果ps对指定的xs做预测并获得预测值
def predict(ps, xs):
# 对每个x计算多项式SUM{ps[i]*x^(n-i)},i从0到n,即获得输入对应的预测值序列
ys_ = np.polyval(ps, xs)
return ys_
# 计算MSE损失,即SUM(0.5*[y-y']^2)
def get_mse_loss(ys, ys_):
return 0.5 * ((ys - ys_) ** 2).sum()
if __name__ == '__main__':
# 房子面积,房子价格
xs, ys = [], []
# 读入数据
for line in open(BASE_DIR + "/data/z1/prices.txt"):
x, y = line.split(",")
xs.append(float(x))
ys.append(float(y))
xs, ys = np.array(xs), np.array(ys)
# 横坐标(房子面积)标准化
xs = (xs - xs.mean()) / xs.std()
fig, ax = plt.subplots(1, 1, figsize=(12, 4))
ax.scatter(xs, ys, c="k", s=20) # c=点的颜色,s=点的大小
# 生成拟合曲线的采样点
x0s = np.linspace(-2, 4, 100)
# 用于拟合数据点的多项式的系数n=1,n=4,n=10
degs = (1, 4, 10)
for d in degs:
# 使用不同次的多项式做训练,并对采样点做预测以绘制拟合曲线
ps = train(xs, ys, d)
y0s_ = predict(ps, x0s)
ax.plot(x0s, y0s_, label="多项式次数={}".format(d))
# 计算在这个训练结果(ps)下原样本的MSE损失
ys_ = predict(ps, xs)
loss = get_mse_loss(ys, ys_)
print("多项式次数={},MSE损失={}".format(d, loss))
# 限制x轴和y轴范围
plt.xlim(-2, 4)
plt.ylim(1e5, 8e5)
plt.legend() # 用于显示图例
plt.show()
运行结果:
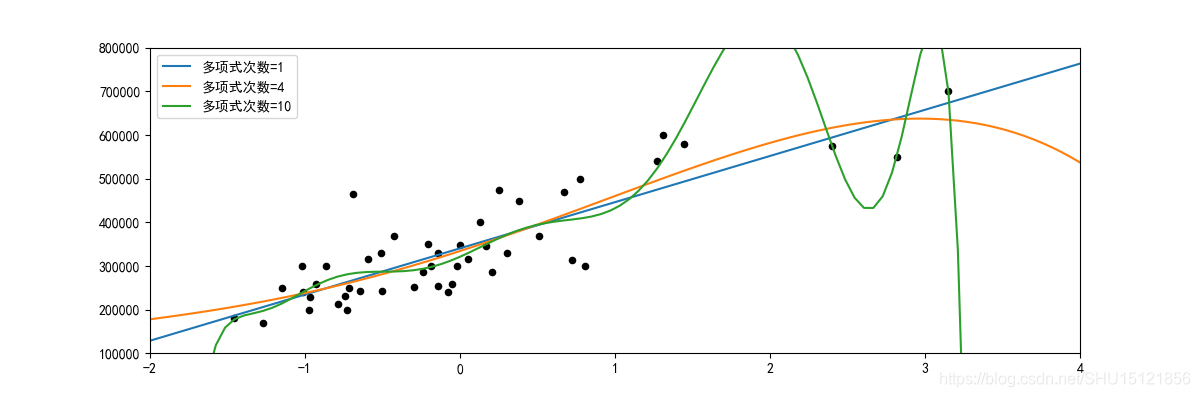
多项式次数=1,MSE损失=96732238800.35297
多项式次数=4,MSE损失=94112406641.6774
多项式次数=10,MSE损失=75874846680.09279
从图上拟合情况来看,选取次数太高的多项式去拟合数据点显然会造成严重的过拟合。