机器学习：多项式回归（基础理解）

一、多项式回归的思想

　1）什么是多项式回归法？

• 样本特征和值（y）呈非线性关系，这种关系的数学模型是一个多项式，如：y = ax² + bx + c，其中 x² 可以看做是认为添加的另一个特征。

　2）多项式回归法能解决什么问题？以及怎么解决？

• 解决的问题：拟合不是直线关系而是其它曲线关系的数据；

• 解决方法：与线性回归类似，假设特征与值（y）呈一个多项式的数学模型的关系，具体操作时可以看成在线性关系的基础上添加多项式（ ax² ）；

　3）多项式回归法的具体操作步骤？

• 在线性模型（ax + c）的基础上添加多项式（如 ax² ），建立数学模型，其它操作和线性回归一样；

　4）其它

• 线性回归法最大的局限性：要求先假设数据呈线性关系，但实际应用场景中，具有线性关系这么强的假设关系的数据集，相对较少，更多的数据是呈非线性关系；

• 多项式回归法：对线性回归法的改进，使得能处理非线性的问题，做出相应的预测；

• 模型泛化：机器学习中几乎最重要的一个概念；

• 线性回归法：假设数据背后呈线性关系这种规律，找出这种线性规律的具体数学表达式；

• 假设数据关系的前提：先大致判断数据背后的关系，一般将数据可视化后直接观察，可视化的手法是查看每一种特征与值（也就是 y）的关系；

• 在机器学习中，多项式回归算法完全使用线性回归算法的思路，但其关键在于为原来的样本添加了新的特征（如 ax²），而添加的新的特征的方式是原来特征的多项式组合，采用这种方式就可以解决非线性问题；

• 注：在多项式回归算法中，使原始数据集的维度升高，使得算法更好的拟合高维的数据；

二、例

　1）模拟并绘制非线性关系数据集

• import numpy as np
  import matplotlib.pyplot as plt
  
  x = np.random.uniform(-3, 3, size=100)
  X = x.reshape(-1, 1)
  y = 0.5 * x**2 + x * 2 + np.random.normal(0, 1, size=100)
  
  plt.scatter(x, y)
  plt.show()

  

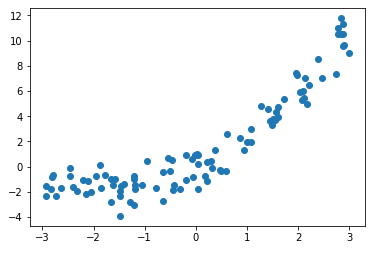
　2）用线性回归拟合数据集

• from sklearn.linear_model import LinearRegression
  
  lin_reg = LinearRegression()
  lin_reg.fit(X, y)
  
  y_predict = lin_reg.predict(X)
  
  plt.scatter(x, y)
  plt.plot(x, y_predict, color='r')
  plt.show()

  

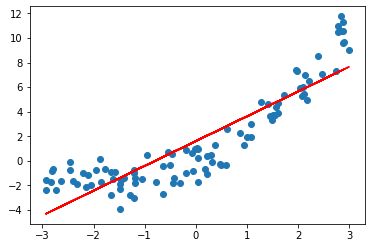
1. 问题：用直线拟合一个有弧度的曲线，拟合效果不好；

　3）采用多项式模型拟合数据

• 为线性模型添加一个特征（多项式 ax²）

  X2 = np.hstack([X, X**2])
  
  lin_reg2 = LinearRegression()
  lin_reg2.fit(X2, y)
  y_predict2 = lin_reg2.predict(X2)
  
  plt.scatter(x, y)
  plt.plot(x, y_predict2, color='r')
  plt.show()

  

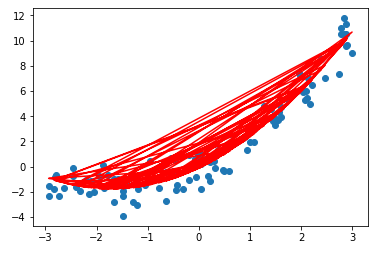
1. 问题：出现不规律的折线图形，而不是根据 x 的从小到大的顺序以此连接折线；
2. 解决方法：将 x 中的数按大小顺序排序后绘制与 y_predict2 的折线关系图；
3. 注：此处对 x 排序后，对应的 y_predict2 中的数据的顺序也要跟着变动，也就是 x 与 y_predict2 的对应关系不变，只是排序；

• 改进绘图方式

  plt.scatter(x, y)
  
  # np.argsort(x)：返回 x 排序后的索引，这个索引是原 x 中数据的索引（更多操作方法，参见 numpy），使得与 x 数据呈对应关系的 y_predict2，也跟着 x 的变化重新排序
  plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
  plt.show()

  

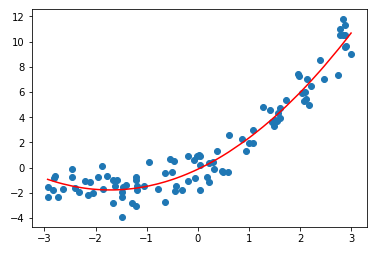
1. np.argsort(x)：返回 x 排序后的索引，这个索引是原 x 中数据的索引（更多操作方法，参见 numpy），使得与 x 数据呈对应关系的 y_predict2，也跟着 x 的变化重新排序；

• 分析

  lin_reg2.coef_
  # 输出：array([1.92399636, 0.56177674])
  
  lin_reg2.intercept_
  # 输出：-0.12289091725257695

1. 第一个系数 1.92399636 是构造数据 X2 中 X 的系数，第二个系数是 X2 中 X**2 的系数，与模拟的关系模型（0.5 * x**2 + x * 2）接近；
2. 得到的系数并不完全等于模拟的关系模型（0.5 * x**2 + x * 2）的系数，这是因为模拟模型时添加了噪音；