判别域代数界面方程法----线性判别函数

在n维特征空间中，特征矢量,线性判别函数的一般形式是

式中：称为权矢量或系数矢量。为简洁起见，上式还可以写成

式中：，,其中x称为增广特征矢量，w成为增广权矢量。此时的增广特征矢量的全体称为增广特征空间。

两类问题

设d(x)为判别函数，待识模式增广特征矢量x可以通过下面判别规则进行分类

等于0时可以任判或拒判。

多类问题

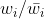两分法

这方法的基本思想是用判别函数将属于Wi类的与不属于的分开。将问题变成多个两类问题，如果模式是线性可分的，一般需要建立c-1个独立的判别函数，为方便起见可建立c个判别函数

通过训练，每个判别函数都会具有下面的性质

不难想到，这样划分出来的子区域会有很多的重叠部分，即不确定区，类别越多，不确定区也会越多。因此需要通过多个不等式的联立，才能使判别结果更精确。所以对于c类问题，判决规则为

如果,则判

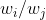两分法

基本思想：对c类中的任意两类和都建立一个判别函数，这两个函数只将两类区分开对其他模式分类是否正确不提供信息。通过训练得到区分两类的判别函数为

它具有性质

显然，的正负并不可以判断出x是属于哪一类，只能判断出x是位于含有类的子区域还是含有类的子区域中，因为在其中一个子区域中还可能含有其他的类域（或一部分）。所以需要通过多个不等式的联立，才能使判别结果更精确，判决规则为

没有不确定去区的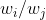两分法

对方法2中的判别函数作下面的处理，令

则对等价于,于是对每一类、均建立一个判别函数di(x),c类问题就有c个判别函数

此时的判别规则为

如果

则

小结

1.当c>3时，比需要更多的判别函数式，这是一个缺点。

2.但是法是将类与其余的c-1类分开，而法则将与，显然法使模式更容易线性可分，这是它的有点。

3.方法⑶判别函数的数目和方法⑴相同，但没有不确定区，分析简单，是最常用的一种方法。方法⑶判别函数的数目和方法⑴相同，但没有不确定区，分析简单，是最常用的一种方法。