线性判别分析(Linear Discriminant Analysis)
在分类器的理论中,贝叶斯分类器是最优的分类器,而为了得到最优的分类器,我们就需要知道类别的后验概率P(Ck|x)。
这里假设fk(x)是类别Ck的类条件概率密度函数,πk 是类别Ck的先验概率,毫无疑问有∑kπk=1。根据贝叶斯理论有:
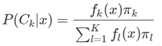
由于πk几乎是已知的,所以对于贝叶斯公式而言,最重要的就是这个类条件概率密度函数fk(x),很多算法之所以不同,主要的就是对这个类条件概率密度函数的参数形式的假设不同,比如:
线性判别分析(LDA)假设fk(x)是均值不同,方差相同的高斯分布
二次判别分析(QDA)假设fk(x)是均值不同,方差也不同的高斯分布
高斯混合模型(GMM)假设fk(x)是不同的高斯分布的组合
很多非参数方法假设fk(x)是参数的密度函数,比如直方图
朴素贝叶斯假设fk(x)是Ck边缘密度函数,即类别之间是独立同分布的
各种算法的不同,基本上都是来至于对类条件概率密度函数的不同,这一点在研究分类算法的时候,一定要铭记在心。
前面已经说过了LDA假设fk(x)是均值不同,方差相同的高斯分布,所以其类条件概率密度函数可以写为:

这里,特征xx的维度为pp维,类别CkCk的均值为μkμk,所有类别的方差为ΣΣ。
在前面提到过,一个线性分类器,在判别式函数δk(x)或者后验概率函数P(Ck|x)上加上一个单调函数f(⋅)后,可以得变换后的函数是x的线性函数,而得到的线性函数就是决策面。LDA所采用的单调变换函数f(⋅)和前面提到的Logistics Regression采用的单调变换函数一样,都是logit 函数:log[p/(1−p)],对于二分类问题有:
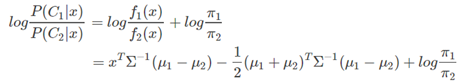
可以看出,其决策面是一个平面。
根据上面的式子,也可以很容易得到LDA的决策函数是:
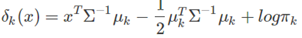
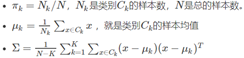
二次判别分析QDA
二次判别函数假设fk(x)是均值不同,方差也不同的高斯分布,和LDA相比,由于Σk是不一样 ,所以其二次项存在,故其决策面为:
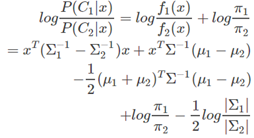
其对应的判别函数为:

使用
# 线性判别式分析
lda = LinearDiscriminantAnalysis(solver='svd', store_covariance=True)
y_pred = lda.fit(X, y).predict(X)
# 二次判别分析
qda = QuadraticDiscriminantAnalysis(store_covariances=True)
y_pred = qda.fit(X, y).predict(X)