模式识别 第四章 —— 线性判别函数
线性可分与线性不可分
就是寻找一个线性判别函数 g ( x ) = α T y g(x) = \alpha^{T}y g(x)=αTy,使对这 n n n个样本的错分概率最小。
如果存在一个权向量 α \alpha α,对所有的 y ∈ ω 1 y \in \omega_{1} y∈ω1,均有 g ( x ) > 0 g(x) > 0 g(x)>0;且对于所有的 y ∈ ω 2 y \in \omega_{2} y∈ω2,均有 g ( x ) < 0 g(x) < 0 g(x)<0。则这组样本是线性可分的,否则为线性不可分的。
如果一个权向量 α ∗ \alpha^{*} α∗满足 α T y > 0 \alpha^{T}y > 0 αTy>0,则 α ∗ \alpha^{*} α∗就是权值空间的一个解向量,所有的解向量组合起来形成的区域就叫解区。很明显,根据线性代数的知识,该解区位于所有样本对应的超平面(这个超平面由 α T y = 0 \alpha^{T}y = 0 αTy=0确定,过原点的)的正侧区域的交集,如下图:
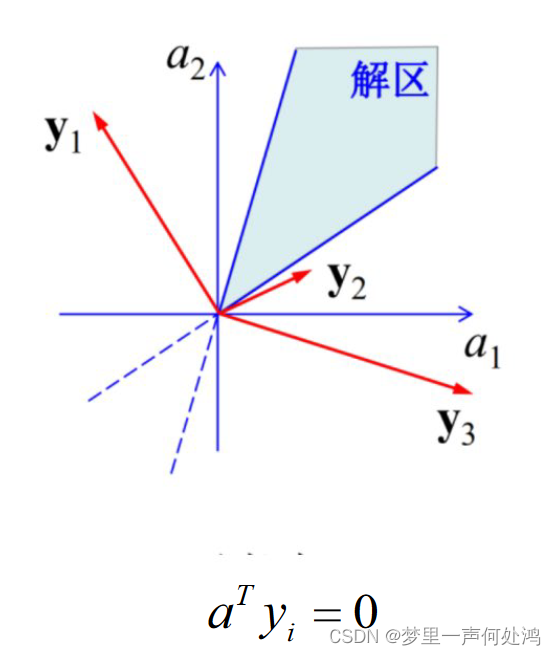
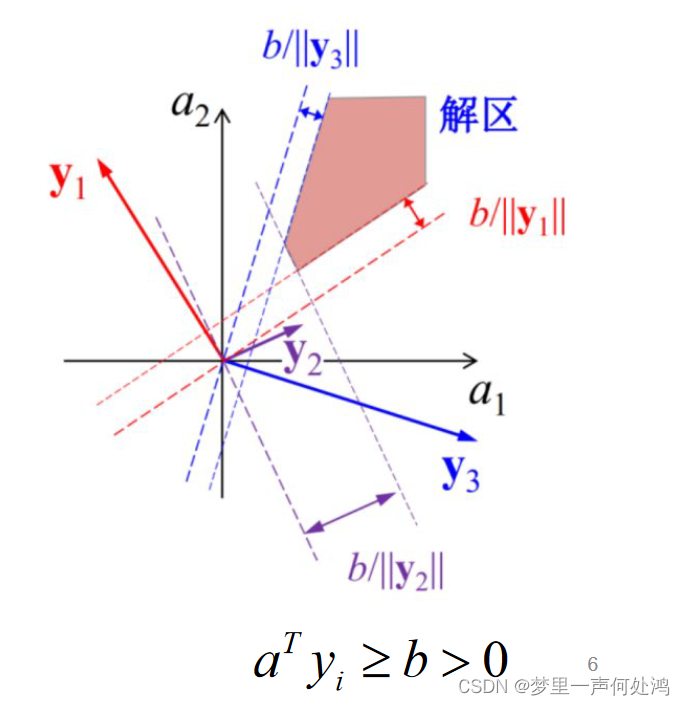
对于那些刚刚恰好大于0的样本来说,可能就未必是正确的分类,为什么呢,因为不可避免的会受到噪声、计算过程中的数值误差等因素的影响,所以这样得到的解区未必是完全正确的有效解,所以有人提出了‘余量’的概念,即在解区的靠近边缘部分留有一定冗余量(如下图),得到更加靠近中间区域的解区,这样产生的结果也许更准确可靠。假设引入的余量为b,且大于0,此时所有的解向量均满足: α T y > b \alpha^{T}y > b αTy>b
感知准则函数
感知器是一种可以直接得到线性判别函数 g ( x ) = ω T x + ω 0 g(x) = \omega^{T}x + \omega_{0} g(x)=ωTx+ω0的线性分类方法.
我们将上面线性判别函数中的样本向量x增加一维常数,我们称为增广样本向量,并记为 y = [ 1 , x 1 , x 2 ⋯ x d ] T y = [1,x_{1},x_{2}\cdots x_{d}]^{T} y=[1,x1,x2⋯xd]T
同样地,对于权向量,也做这样的增广,称之为增广权向量 α = [ 1 , ω 1 , ω 2 ⋯ ω d ] T \alpha = [1,\omega_{1},\omega_{2}\cdots \omega_{d}]^{T} α=[1,ω1,ω2⋯ωd]T
因此,我们有了新的线性判别函数形式 g ( x ) = α T y g(x) = \alpha^{T}y g(x)=αTy。为了求解感知器的准则函数,就是找到一个解向量,使得惩罚函数最小化。对于错分的样本都满足 α T y i < 0 \alpha^{T}y_{i} < 0 αTyi<0,很明显是当其值为0时最小,下面利用机器学习中常用的经典梯度下降方法来迭代;先给出惩罚函数对于解向量的梯度公式:

例1:



例2:

