1. 线性判别函数
- 本章介绍的线性判别函数都归属于判别式模型,即对于分类问题,根据判别函数\(g(x)\)的取值进行判断,比如正数归为第一类,负数与零归为第二类。关于判别式模版与生成式模型的区别可以阅读我以前的[博客])(https://www.cnblogs.com/szxspark/p/8426850.html),最典型的生成式模型是贝叶斯分类器,这个在之前的博客中也有介绍。
在介绍具体算法之前,先了解一下线性判别函数的基本概念。
1.2 线性判别函数基本概念
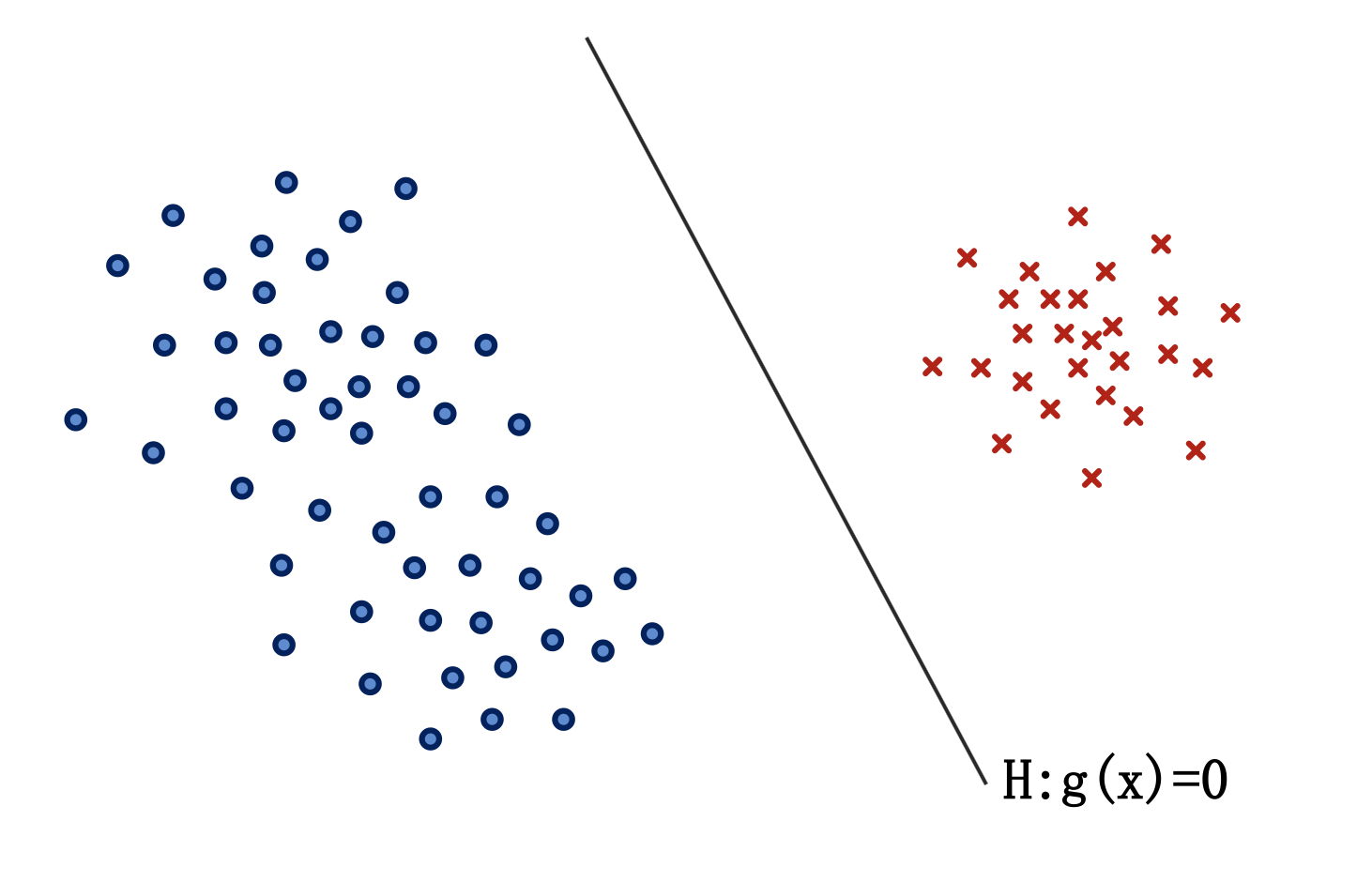
- 对于线性可分情况,线性判别函数\(g(x)\)与判别界面\(H\)如下图所示:
-
- 对于线性不可分情况:
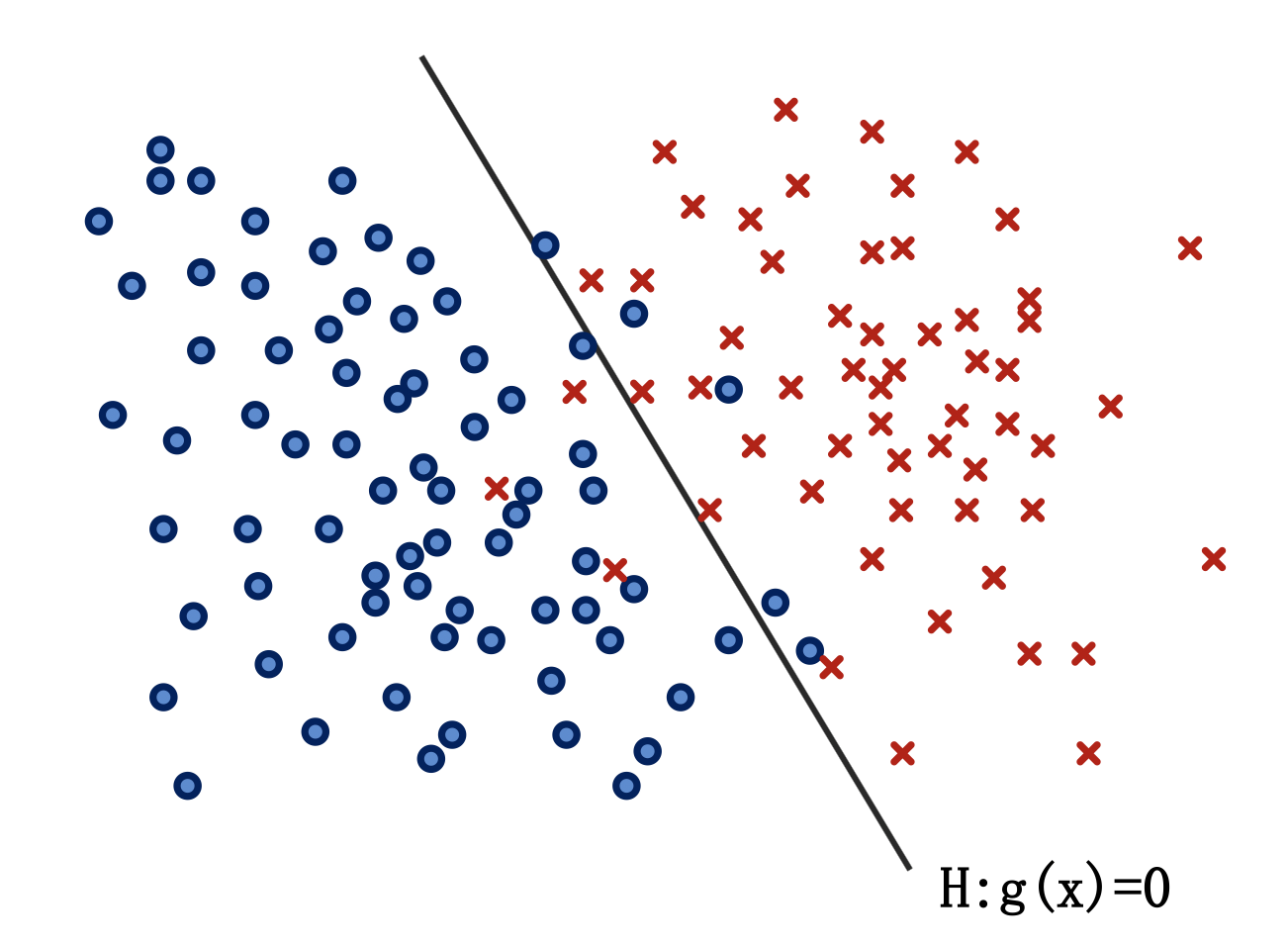
- 线性判别函数的形式化形式为:
\[g ( \mathbf { x } ) = \mathbf { w } ^ { t } \mathbf { x } + w _ { 0 }\]- \(\mathbf { x } = \left( x _ { 1 } , x _ { 2 } , \ldots , x _ { d } \right) ^ { t }\),是特征矢量,\(d\)是特征维度的大小。
- \(\mathbf { w } = \left( w _ { 1 } , W _ { 2 } , \dots , W _ { d } \right) ^ { t }\),是权矢量。
- \(W _ { 0 }\) 是偏置。
- 线性判别函数的增广形式(便于书写,便于设计目标函数):
\[g ( \mathbf { y } ) = \mathbf { a } ^ { t } \mathbf { y }\]- \(\mathbf { y } = \left( 1 , x _ { 1 } , x _ { 2 } , \ldots , x _ { d } \right) ^ { t }\),是增广的特征矢量,在原始向量前插\(1\)即可。
\(\mathbf { a } = \left( w _ { 0 } , w _ { 1 } , W _ { 2 } \dots , W _ { d } \right) ^ { t }\),是增广的权矢量。
在学习该增广形式的时候,我曾思考过,既然可以将将线性函数转化为两个向量的点乘,那在深度学习中(以pytorch为例),设计线性层(nn.Linear)时为什么还要令参数bias=True,直接不需要偏置,在输入向量中拼接一个维度(值为1)岂不是更加方便。答案当然是否定,我仔细思考后发现,如果这么做的话,对于每一个输入对会有一个独立的bias,因为新拼接的“1”值会随着反向传播进行迭代更新(每个输入的更新结果不同),此时bias便失去了意义,不再是与线性函数函数绑定,而是变成了输入的一个特征。
- 两类问题的线性判别准则:
\[g ( \mathbf { x } ) = \mathbf { w } ^ { t } \mathbf { x } + w _ { 0 } \left\{ \begin{array} { l l } { > 0 , } & { \mathbf { x } \in \omega _ { 1 } } \\ { < 0 , } & { \mathbf { x } \in \omega _ { 2 } } \\ { = 0 } & {拒识 } \end{array} \right.\] - 线性分类器的分类界面三维空间可视化:
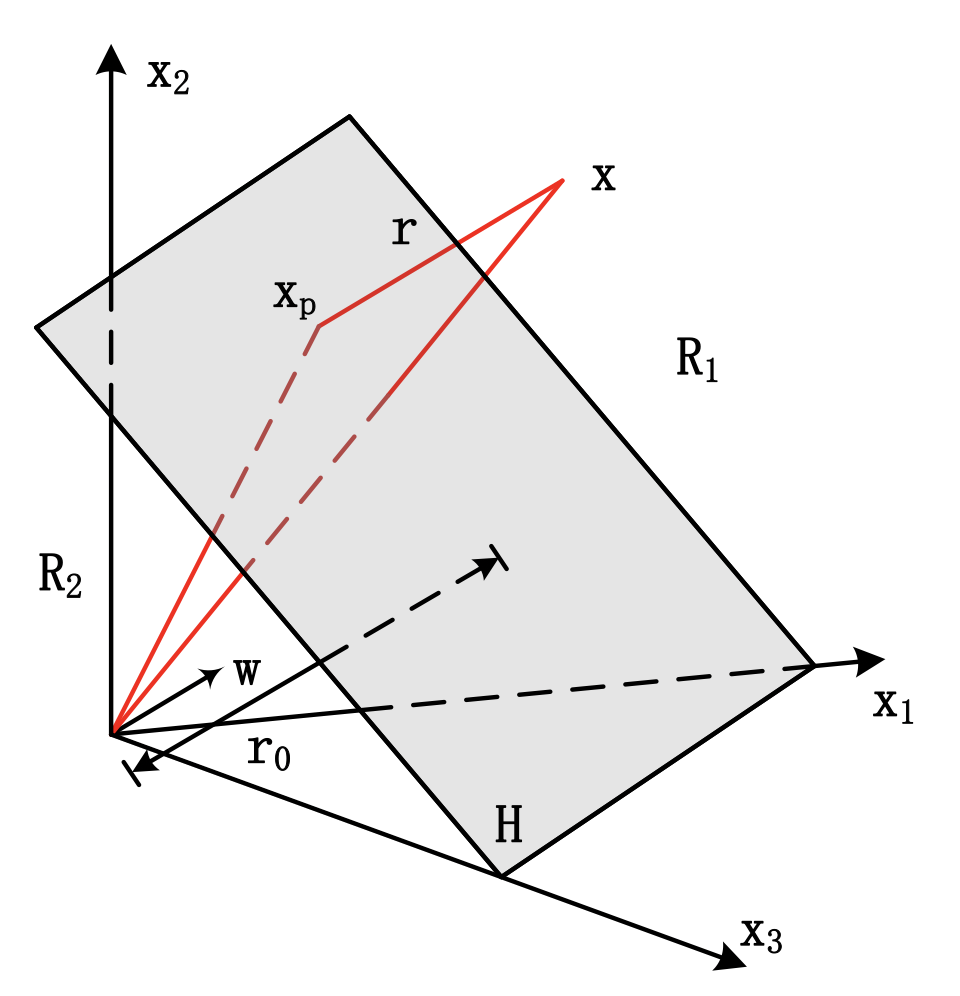
该界面有几个特点:
1.线性分类界面\(H\)是\(d\)维空间中的一个超平面;
2.分类界面将\(d\)维空间分成两部分,\(R_1\),\(R_2\)分别属于两个类别;
3.判别函数的权矢量\(w\)是一个垂直于分类界面\(H\)的矢量,其方向指向区域\(R_1\) ;
4.偏置\(w_0\)与原点到分类界面\(H\)的距离\(r_0\)有关:
\[r _ { 0 } = \frac { w _ { 0 } } { \| \mathbf { w } \| }\]
1.3 线性判别函数的学习
- 以下内容全部采用增广形式的写法进行介绍。
- 线性判别函数的学习目的,其实就是想通过\(n\)个训练样本\(\mathbf { y } _ { 1 } , \mathbf { y } _ { 2 } , \dots , \mathbf { y } _ { n }\),来确定一个判别函数\(g ( \mathbf { y } ) = \mathbf { a } ^ { t } \mathbf { y }\)的权矢量\(a\)。其中n个样本集合来源于两个不同类别。
- 在线性可分的情况下,希望得到的判别函数能够将所有的训练样本正确分类。
- 线性不可分的情况下,判别函数产生错误的概率最小。
- 判别函数的非规范化形式:
\[\left\{ \begin{array} { l l } { \mathbf { a } ^ { t } \mathbf { y } _ { i } > 0 , } & { \mathbf { y } _ { i } \in \omega _ { 1 } } \\ { \mathbf { a } ^ { t } \mathbf { y } _ { i } < 0 , } & { \mathbf { y } _ { i } \in \omega _ { 2 } } \end{array} \right.\] 判别函数的规范化i形式:
\[\left\{ \begin{array} { c l } { \mathbf { a } ^ { t } \mathbf { y } _ { i } > 0 , } & { \mathbf { y } _ { i } \in \omega _ { 1 } } \\ { - \mathbf { a } ^ { t } \mathbf { y } _ { i } > 0 , } & { \mathbf { y } _ { i } \in \omega _ { 2 } } \end{array} \right.\]- 在之后的感知器算法于LMSE算法中,均依据规范化的形式进行介绍,规范化后会使得目标函数形式比较简单。
- 规范化是在输入数据上进行,将属于第二个类别的数据乘上\(-1\)即可。
- 需要注意,因为本节内容是在函数的增广形式下进行介绍,因此在规范化之前需要对于每个类别的数据都拼接一个特征“1”。