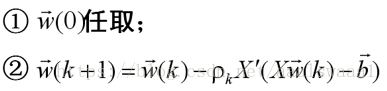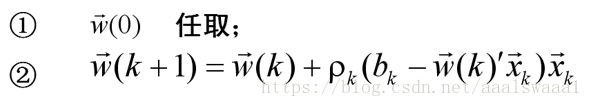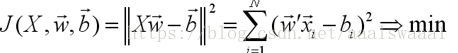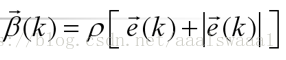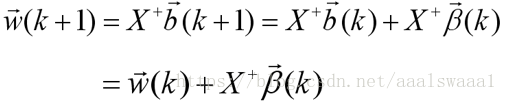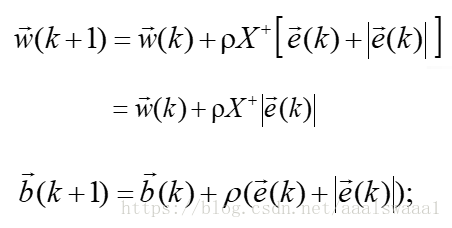最小平方误差准则及W-H算法
针对等式方程组
建立二次准则函数。若X有逆,由上式可得.但通常运用最优化技术求解权矢量w。基于方程组
,构造平方3误差准则函数
显然,若,那么此时的J=minJ(w)=0;但是,如果有令不等的
,则J(w)>0。当b给定后,可以采用最优化技术搜索J(w)的极小值点以求解等式方程组
。如果方程组有唯一解,极小值点就是该解,说明训练模式集是线性可分的;若无解,极小值点就是最小二乘解。由于
的各项取平方,上述准则实际上是将各模式到界面的距离平方和最小化,即时训练模式是线性可分的该算法也不能保证求得的权矢量对所有模式都能正确分类,以及误分模式个数最少。
梯度法
J(w)的梯度为
梯度下降算法迭代公式为:
可以证明,当=
(
为任意正的常熟),则该算法使权矢量序列{w(k)}收敛于
,满足
为了减少计算量和存储量,可以仿照单样本修正法:
由于
有
此算法通常成为W-H算法。
H-K算法
此算法是针对前述一些算法不足的改进。H-K算法仍然使用最小平方误差准则
这种算法将准则函数J(·)看成矢量w和b的函数,在迭代过程中对2者都进行修改调整,用最优化技术求得使准则函数J取极小值的和
。
如果训练模式集是线性可分的,该算法所求得的解矢量对所有模式都能正确分类,且可使J(·)=0。仍采用梯度下降法。易知:
b(k)的迭代公式为:
调整规则是
若Xw(k)-b(k)≤0,则β(k)=0;
若Xw(k)-b(k)>0,则;
若Xw(k)-b(k)仅某些分量为正值,,则只增大与这些正分量对应的b的分量。
记误差分量
于是上面的调整规则可统一写为
由伪逆法知道
从而有关于w的迭代公式
算法步骤
1.将训练样本符号规范化,得X求伪逆
2.置初值b(1)>0,k=1,ρ=1/2
3.计算:
4.判断:若,继续下一步;
若,停止,得到
;
若e(k)的负的分量停止吧变为正值或各分量均为负值,停止。
5.计算
6.令k=k+1,返回3