算法导论chapter12 二叉搜索树课后习题答案详解

英文答案https://wenku.baidu.com/view/000b5347b9f3f90f76c61b9b.html

12.1

1. 定义

2. 构建方法：12.1-1，2

3. 遍历：12.1-3，4

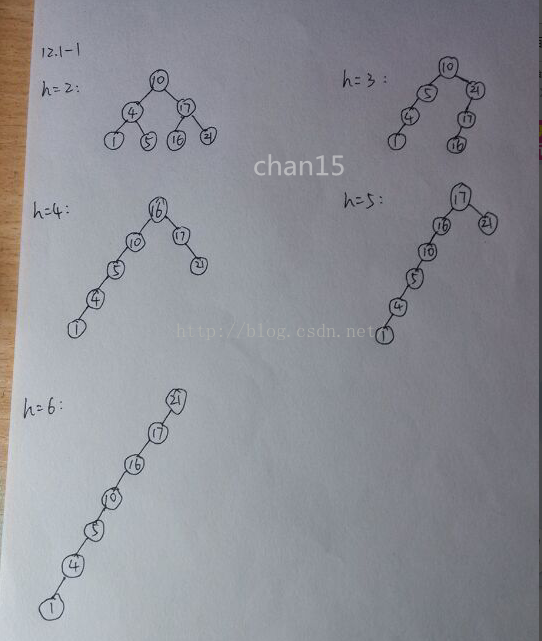
12.1-1 对于关键字集合 { 1,4,5,10,16,17,21 }，分别画出高度为2、3、4、5 和 6 的二叉搜索树。
ANSWER：

12.1-2 二叉搜索树性质与最小堆性质（见 6.1 节）之间有什么不同？能使用最小堆性质在 O( n ) 时间内按序输出一颗有 n 个结点的关键字吗？可以的话，请说明如何做，否则解释理由。
ANSWER：
① 最小堆只是根结点比儿子的关键字小，不能直接通过遍历得到排序结果。二叉搜索树可以通过中序遍历得到升序排序。
② 不能在 O( n ) 时间内按序输出，因为最小堆提取根结点后需要用 O( lgn ) 时间维持最小堆的性质。而且基于比较的排序算法下限 O( nlgn )。

12.1-3 设计一个执行中序遍历的非递归算法。（提示：一种容易的方法是使用栈作为辅助数据结构；另一种较复杂但比较简洁的做法是不使用栈，但要假设能测试两个指针是否相等。）
ANSWER：

# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution94(object):              ######二叉树中序遍历的非递归方法，用栈
    def inorderTraversal(self, root):   #先把根节点入栈，如果左子树一直不为空，就一直入栈，直到 
                                  ##把所有左节点入栈，然后pop栈顶元素，指针指向栈顶元素的右子树
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        stack=[]
        res=[]
        if not root:
            return []
        while root or stack:
            while root:
                stack.append(root)
                root=root.left
            if stack:
                a=stack.pop()
                root=a.right
                res.append(a.val)
        return res

复杂度分析

二叉树遍历的非递归实现，每个结点只需遍历一次，故时间复杂度为O(n)。而使用了栈，空间复杂度为二叉树的高度，故空间复杂度为O(n)。

Morris遍历算法最神奇的地方就是，只需要常数的空间即可在O(n)时间内完成二叉树的遍历。O(1)空间进行遍历困难之处在于在遍历的子结点的时候如何重新返回其父节点？在Morris遍历算法中，通过修改叶子结点的左右空指针来指向其前驱或者后继结点来实现的。

12.1-4 对于一课有 n 个结点的树，请设计在 Θ( n ) 时间内完成的先序遍历算法和后序遍历算法。

ANSWER：

# 先序打印二叉树（递归）
def preOrderTraverse(node):
    if node is None:
        return None
    print(node.val)
    preOrderTraverse(node.left)
    preOrderTraverse(node.right)


# 后序打印二叉树（递归）
def postOrderTraverse(node):
    if node is None:
        return None
    postOrderTraverse(node.left)
    postOrderTraverse(node.right)
    print(node.val)

12.1-5 因为在基于比较的排序模型中，完成 n 个元素的排序，其最坏情况下需要 Ω( nlgn ) 时间。试证明：任何基于比较的算法从 n 个元素的任意序列中构造一棵二叉搜索树，其最坏情况下需要 Ω( nlgn ) 的时间。
ANSWER：
反证法：

       假设构造一棵二叉搜索树的最坏情况的时间 T( n ) < c1nlgn，而中序遍历二叉搜索树只需要 Θ( n ) 的时间，所以通过构造二叉搜索树的比较排序时间为 T( n ) + Θ( n )< c2nlgn，与基于排序模型中，n 个元素的排序最坏情况的 Ω( nlgn ) 时间矛盾。假设不成立。得证

另解：

       构造二叉查找树是对一组杂乱无章的数据排序的过程，而基于比较的排序的时间为Ω(nlgn)，所以构造这棵树也要Ω(nlgn)。   

       (1)如果二叉排序树T为空，则创建一个关键字为k的结点，将其作为根结点。
       (2)否则将k和根结点的关键字进行比较，如果相等则返回，如果k小于根结点的关键字则插入根结点的左子树中，否则插入根结点的右子树中。

12.2

查找

前驱节点

找到该节点
若一个节点有左子树，那么该节点的前驱节点是其左子树中val值最大的节点（也就是左子树中所谓的rightMostNode）
若一个节点没有左子树，那么判断该节点和其父节点的关系 
 2.1 若该节点是其父节点的右边孩子，那么该节点的前驱结点即为其父节点。 
 2.2 若该节点是其父节点的左边孩子，那么需要沿着其父亲节点一直向树的顶端寻找，直到找到一个节点P，P节点是其父节点Q的右边孩子（可参考例子2的前驱结点是1），那么Q就是该节点的后继节点

后继节点

找到该节点
若一个节点有右子树，那么该节点的后继节点是其右子树中val值最小的节点（也就是右子树中所谓的leftMostNode）
若一个节点没有右子树，那么判断该节点和其父节点的关系 
2.1 若该节点是其父节点的左边孩子，那么该节点的后继结点即为其父节点 
2.2 若该节点是其父节点的右边孩子，那么需要沿着其父亲节点一直向树的顶端寻找，直到找到一个节点P，P节点是其父节点Q的左边孩子（可参考例子2的前驱结点是1），那么Q就是该节点的后继节点
 

最大值节点

搜索右子树指导NULL

最小值节点

搜索左子树指导NULL

12.2-1 假设在某二叉查找树中，有1到1000之间的一些数，现要找出363这个数。下列的结点序列中，哪一个不可能是所检查的序列？
a)2,252, 401,398,330,344,397,363               b)924,220,911,244,898,258,362,363
c)925,202,911,240,912,245,363                   d)2,399,387,219,266,382,381,278,363
e)935,278,347,621,299,392,358,363

abc三个数，递增，递减 或c在ab中间合法，c比ab都大或者都小不合法
c. 911与912不符合二叉查找树规则。e.347与299不符合二叉查找树规则。

12.2-2 写出TREE-MINIMUM和TREE-MAXIMUM过程的递归版本。
 

def findMin(self, root):
        '''查找二叉搜索树中最小值点'''
        if root.left:
            return self.findMin(root.left)
        else:
            return root
        
 def findMax(self, root):
        '''查找二叉搜索树中最大值点'''
        if root.right:
            return self.findMax(root.right)
        else:
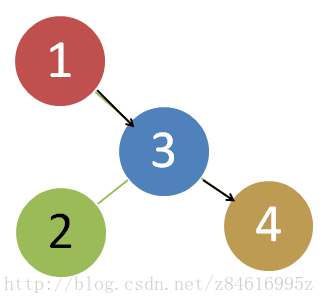
            return root

12.2-4 Bun教授认为他发现了二叉查找树的一个重要性质。假设在二叉查找树中，对某关键字k的查找在一个叶结点结束，考虑三个集合：A，包含查找路径左边的关键字；B，包含查找路径上的关键字；C，包含查找路径右边的关键字。Bunyan教授宣称，任何三个关键字a∈A，b∈B,c∈C,必定满足a≤b≤c.请给出该命题的一个最小可能的反例。

查找路径(1→3→4)∈b ,2∈a,所以a>b。

12.2-5 证明：如果二叉查找树中的某个结点有两个子女，则其后继没有左子女，其前驱没有右子女。
设这个结点为x其左孩子x1右孩子x2，则有key[x1]≤key[x]≤key[x2]。存在x的右子树，则后继为右子树中数值最小的左儿子x3，若后继x3有左子女x4,则key[x4]≤key[x3],而key[x的右子树]≥key[x],所以key[x3]≥key[x4]≥key[x],那么x4就为结点x的后继而非x3了。前驱没有右子女也有类似的证明。这里略过。

12.2-6 考虑一棵其关键字各不相同的二叉查找树T，证明：如果T中某个结点x的右子树为空，且x有一个后继y，那么y就是x的最低祖先，且其左孩子也是x的祖先。(注意每个节点都是它自己的祖先)

最低祖先节点就是从根节点遍历到给定节点时的最后一个相同节点，或最近公共父节点
若x是其后继y的左孩子，那么key[x]≤key[y],所以y是x的最低祖先，y的左孩子为x的祖先也就是x本身。
若x是其后继y的右孩子，那么key[x]≥key[y],这明显与后继定义矛盾，y是x的前驱。所以x不可能是后继y的右子树。
若x是y的左孩子y1的右孩子，那么有key[y1]≤key[x],后继y的左孩子y1是x的祖先，同时y是x的最低祖先。

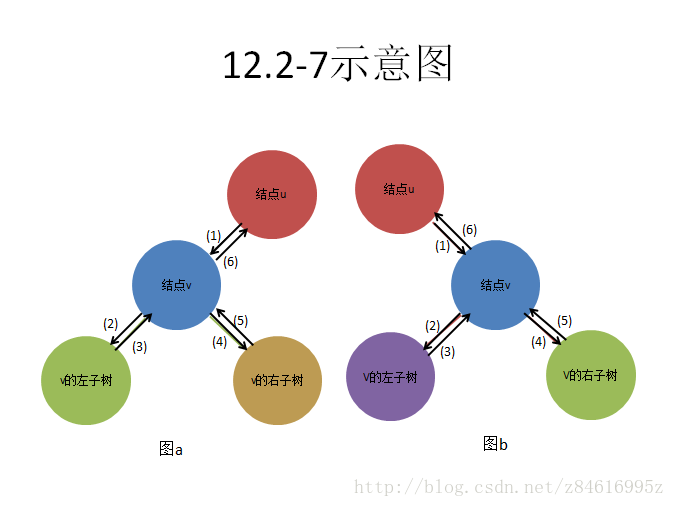
12.2-7 对于一棵包含n个结点的二叉查找树，其中序遍历可以这样来实现：先用TREE-MINIMUM找出树中的最小元素，然后再调用n-1次TREE-SUCCESSOR。证明这个算法的运行时间为θ(n).

这个图是任意结点树中的一个小部分，但是他们的情况是类似的，都是从1-6顺序遍历的。本题的关键是这个算法在一个包含n个结点的二叉查找树的n-1个边上，通过这n-1分支中的每条边至多2次（扫描过的路径上有节点未被标记则一定由远及近回来标记）（对于一棵子树，a若需要先进入最后退出，考虑访问时有连续的后继，则回退的时候走k步，若不连续的后继回退的时候被标记为后继；b若不需要进入后退出则有些边不需要走两次），也就是说总时间是T<h+2(n-1)=lgn+2(n-1)<cn=>T(n)=O(n)

12.2-8证明：在一棵高度为h的二叉查找树中，无论从哪一个结点开始，连续k次调用TREE-SUCCESSOR所需时间都是O(k+h).
如果简单的利用定义：每调用一次该函数就需要O(h)时间，调用k次就需要O(kh)时间。这种想法是没有深入分析题目中函数具体调用过程。如果明白12.2-7题目核心内容。就知道，除了第一次调用该函数需要O(h)时间外，其余的连续k-1次遍历了连续的k-1个结点，这k-1个结点有k-2个边，而每条边最多遍历2次。所以总时间T=O(h)+2(k-2)=O(h+k).

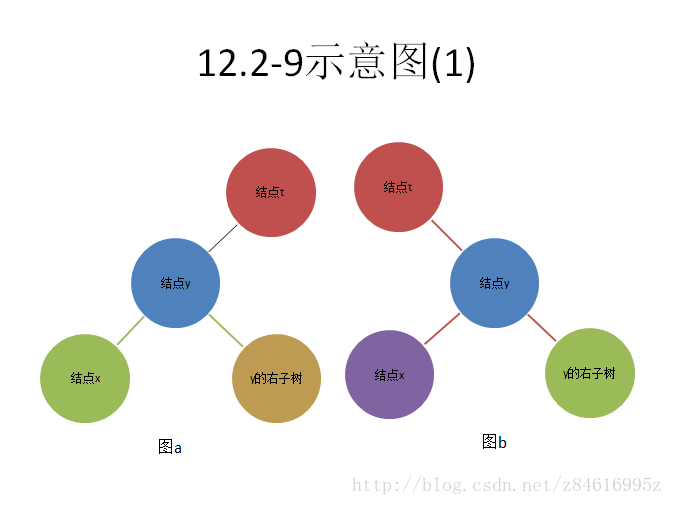
12.2-9 设T为一棵其关键字均不相同的二叉查找树，并设x为一个叶子结点，y为其父结点。证明：key[y]或者是T中大于key[x]的最小关键字，或者是T中小于key[x]的最大关键字

x是y的左孩子，y是在结点t的左子树上，如图a表达的关系可知：key[x]≤key[y]≤key[y的右子树]≤key[t],可见 "key[y]或者是T中大于key[x]的最小关键字" .如图b表达关系可知：key[t]≤key[x]≤key[y]≤key[y的右子树]。也得到相同的答案，无非如图ab两种情况。
           
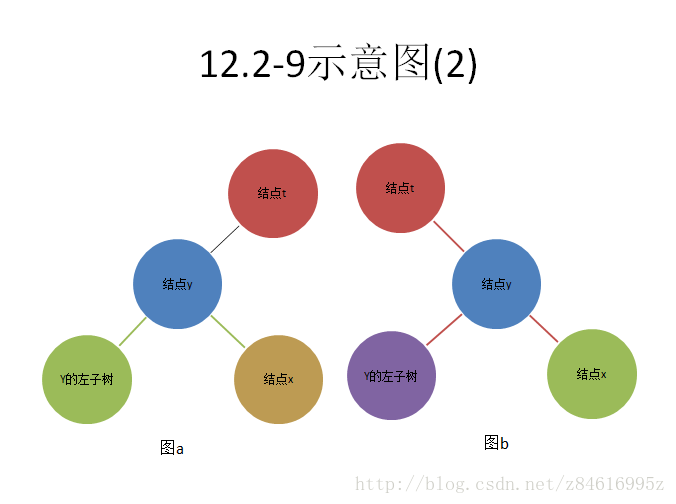
x是y的右孩子，y是在结点t的左子树上，如图a表达的关系可知：key[y的左子树]≤key[y]≤key[x]≤key[t],可见 "或者key[y]是T中小于key[x]的最大关键字" .如图b表达关系可知：key[t]≤key[y的左子树]≤key[y]≤key[x],也可以得到相同的答案。 无非如图ab两种情况。