《算法导论》学习（十五）----二叉搜索树（C语言）

---

前言

本文主要讲解了二叉搜索树，并且用C语言是实现了它的所有基本操作函数，给出了C语言代码

---

一、二叉搜索树

1.什么是二叉搜索树？

二叉搜索树是一颗二叉树，它是链表存储结构，同时满足特定的数据性质（见下）

顾名思义，二叉搜索树有很好的搜索性能，有诸多应用
它的操作函数有：

1.中序遍历（输出有序数据序列）
2.返回最大最小值
3.搜索值
4.返回某个结点的左右顺序统计量
5.插入，删除结点

2.二叉搜索树有什么优势？

（1）应用

1.作为字典存储数据，提供插入，删除，搜索功能
2.输出排好序的序列
3.作为优先队列
4.等等

（2）时间性能

一般情况下，它的所有操作函数的时间代价都是：
$$\begin{gathered} T(n)=O(h)=O(lgn) \\ 其中h为期望树高,h=O(lgn) \end{gathered}$$

3.二叉搜索树的数据特点

设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点，那么$y.key⩽x.key$。如果y是x右子树中的一个结点，那么$y.key⩾x.key$。

它本质上是维护一个局部的有序。这个局部的有序有点类似于堆。

（1）二叉搜索树与堆的数据性质的区别

1.二叉搜索树是将所有小于等于的结点放到左子树，所有大于等于的结点放到右子树
2.堆是在维护一个局部最值，即双亲结点永远要大于（最小堆是小于）孩子结点

具体可以参考文章：
《算法导论》学习（七）----堆排序和优先队列（C语言）

二、二叉搜索树的操作函数（C语言）

1.数据结构

数据结构包涵三个部分：

1.存储key值
2.指向左孩子结点的指针
3.指向有孩子结点的指针
4.指向父亲结点的指针

//定义二叉搜索树的结构
typedef struct STree
{
    
    
	int key;//结点的值 
	STree *p;//指向双亲结点 
	STree *left;//指向左孩子结点 
	STree *right;//指向有孩子结点 
}ST; 

2.中序遍历二叉搜索树

中序遍历的规则：
1.从横向来看：先遍历左子树，再遍历本结点，再遍历右子树
2.从竖向来看：先右下的叶子节点，再向上到根结点，再到坐下的叶子结点

二叉搜索树通过中序遍历，其结果是一个从小到大的有序数列。

（1）中序遍历

//中序遍历二叉搜索树
void inorder_tree_walk(ST *x)
{
    
    
	//由于二叉搜索树的特点
	//使用中序遍历的结果是从大到小的有序排列 
	if(x!=NULL)
	{
    
    
		//先遍历左子树 
		inorder_tree_walk(x->left);
		//遍历本结点 
		printf("%5d",x->key);
		//遍历右子树 
		inorder_tree_walk(x->right);
	}
	else
	{
    
    
		return;
	}
}

（2）打印遍历结果

//打印二叉搜索树
void print_tree(ST *x)
{
    
    
	inorder_tree_walk(x);
	printf("\n");	
} 

3.查找数据

查找到该结点，就返回它的地址信息。
没有查到就返回NULL

（1）查找数据函数

//在二叉搜索树中查找数据
ST *tree_search(ST *x,int k)
{
    
    
	//循环结束条件就是
	//1.结点指针为空
	//2.结点指针指向k结点 
	while(x!=NULL&&x->key!=k)
	{
    
    
		//如果k小于本结点，那么向左子树搜索 
		if(k<x->key)
		{
    
    
			x=x->left;
		}
		//如果k大于等于本结点，那么向右子树搜索
		else
		{
    
    
			x=x->right;
		}
	}
	return x;
}

（2）打印查找信息

//打印查找信息
void print_search(ST *x)
{
    
    
	if(x==NULL)
	{
    
    
		printf("there is no data in tree\n");
	}
	else
	{
    
    
		printf("data is %5d,the address is 0x%x\n",x->key,x);
	}
}

4.得到最大值

返回最大值的地址
根据二叉搜索树的性质，最大值是最右最下的叶子结点

//得到最大值
ST *tree_max(ST *x)
{
    
    
	//最右最下的那个叶子结点就是最大值 
	while(x->right!=NULL)
	{
    
    
		x=x->right;
	}
	return x;
} 

5.得到最小值

返回最小值的地址
根据二叉搜索树的性质，最小值是最左最下的叶子结点

//得到最小值
ST *tree_min(ST *x)
{
    
    
	//最左最下的那个叶子结点就是最小值 
	while(x->left!=NULL)
	{
    
    
		x=x->left;
	}
	return x;
} 

6.找到后继结点

后继结点的定义：
后继结点就是所有大于该结点的树节点中最小的那个

//得到指定结点x的后继结点
//后继结点就是所有大于该结点树节点中最小的那个
ST *tree_successor(ST *x)
{
    
    
	//如果该结点有右子树，那么后继就是右子树的最小值 
	if(x->right!=NULL)
	{
    
    
		return tree_min(x->right);
	}
	ST *y=x->p;
	//如果没有右子树，那么后继结点就是该结点的一个上层结点
	//而且该结点一定是这个上层结点的左子树中的结点
	//那么后继就是第一个满足条件的祖先结点 
	while(y!=NULL&&x==y->right)
	{
    
    
		x=y;
		y=y->p;
	}
	return x; 
}

7.找到前驱结点

前驱结点的定义：
前驱结点就是所有小于该结点的树节点中最大的那个

//得到指定结点x的前驱结点
//前驱结点就是所有小于该结点树节点中最大的那个
ST *tree_precursor(ST *x)
{
    
    
	//如果该结点有左子树，那么前驱就是左子树的最大值 
	if(x->left!=NULL)
	{
    
    
		return tree_max(x->left);
	}
	ST *y=x->p;
	//如果没有左子树，那么前驱结点就是该结点的一个上层结点
	//而且该结点一定是这个上层结点的右子树中的结点
	//那么前驱就是第一个满足条件的祖先结点 
	while(y!=NULL&&x==y->left)
	{
    
    
		x=y;
		y=y->p;
	}
	return x; 
}

8.插入元素到树

//给树中插入函数
ST *tree_insert(ST *x,int k)
{
    
    
	ST *y=NULL;
	ST *head=x;
	//如果是空结点，那么直接连接 
	if(x==NULL)
	{
    
    
		//动态分配空间 
		y=(ST *)malloc(sizeof(ST));
		y->key=k;
		y->left=NULL;
		y->p=NULL;
		y->right=NULL;
		x=y;
		return x;
	}
	//如果树不为空
	//那么按照搜索树的规则，找到要插入对象的位置
	//该位置是一个叶子结点 
	while(x!=NULL)
	{
    
    
		y=x;
		if(x->key>k)
		{
    
    
			x=x->left;
		}
		else
		{
    
    
			x=x->right;
		}
	}
	//分配空间 
	x=(ST *)malloc(sizeof(ST));
	x->key=k;
	x->p=y;
	x->left=NULL;
	x->right=NULL;
	if(y->key>k)
	{
    
    
		y->left=x;
	}
	else
	{
    
    
		y->right=x;
	}
	return head;
}

9.将一个子树替换为另外一个子树

该函数是为删除函数做准备的，删除函数需要大量调用
在删除函数中，它的功能是将u结点从树中分割出来，并且将以v结点为根结点的子树替换u结点的位置

//将一颗子树替换为另一颗子树
//u是被替换子树根结点
//v是替换子树根结点
void ctree_change(ST *x,ST *u,ST *v)
{
    
    
	if(x==u)
	{
    
    
		x=v;
	}
	else if(u==u->p->left)
	{
    
    
		u->p->left=v;
	}
	else
	{
    
    
		u->p->right=v;
	}
	if(v!=NULL)
	{
    
    
		v->p=u->p;
	}
}

10.删除结点

//删除一个结点
void tree_delet(ST *x,int k)
{
    
    
	ST *k_p;
	k_p=tree_search(x,k);
	if(k_p==NULL)
	{
    
    
		printf("there is no k in tree\n");
	}
	else
	{
    
    
		//如果没有左子树
		//那么直接用右子树替换该子树 
		if(k_p->left==NULL)
		{
    
    
			ctree_change(x,k_p,k_p->right);
			free(k_p);
		}
		//如果没有右子树
		//那么直接用左子树替换该子树
		else if(k_p->right==NULL)
		{
    
    
			ctree_change(x,k_p,k_p->left);
			free(k_p);
		}
		else
		{
    
    
			ST *temp=NULL;
			//找到后继结点 
			temp=tree_min(k_p->right);
			if(temp->p!=k_p)
			{
    
    
				//将后继结点提取出来 
				ctree_change(x,temp,temp->right);
				//将后继结点与被删除结点的右子树相连 
				temp->right=k_p->right;
				temp->right->p=temp;
			}
			//提取被删除结点 
			ctree_change(x,k_p,temp);
			//将后继结点与被删除结点的左子树连接 
			temp->left=k_p->left;
			temp->left->p=temp;
			free(k_p);
		}
	}
} 

三、二叉搜索树的C语言例子

1.实际执行结果

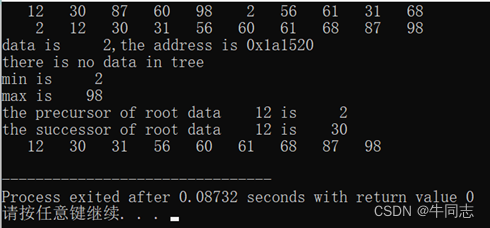
2.C语言代码

#include<stdio.h>
#include<stdlib.h>
#include<time.h>



//输入的规模 
#define SIZE 10
//随机数的范围是0~LIM-1 
#define LIM 100 



//定义二叉搜索树的结构
typedef struct STree
{
    
    
	int key;//结点的值 
	STree *p;//指向双亲结点 
	STree *left;//指向左孩子结点 
	STree *right;//指向有孩子结点 
}ST; 



//中序遍历二叉搜索树
void inorder_tree_walk(ST *x)
{
    
    
	//由于二叉搜索树的特点
	//使用中序遍历的结果是从大到小的有序排列 
	if(x!=NULL)
	{
    
    
		//先遍历左子树 
		inorder_tree_walk(x->left);
		//遍历本结点 
		printf("%5d",x->key);
		//遍历右子树 
		inorder_tree_walk(x->right);
	}
	else
	{
    
    
		return;
	}
}



//打印二叉搜索树
void print_tree(ST *x)
{
    
    
	inorder_tree_walk(x);
	printf("\n");	
} 



//在二叉搜索树中查找数据
ST *tree_search(ST *x,int k)
{
    
    
	//循环结束条件就是
	//1.结点指针为空
	//2.结点指针指向k结点 
	while(x!=NULL&&x->key!=k)
	{
    
    
		//如果k小于本结点，那么向左子树搜索 
		if(k<x->key)
		{
    
    
			x=x->left;
		}
		//如果k大于等于本结点，那么向右子树搜索
		else
		{
    
    
			x=x->right;
		}
	}
	return x;
}



//打印查找信息
void print_search(ST *x)
{
    
    
	if(x==NULL)
	{
    
    
		printf("there is no data in tree\n");
	}
	else
	{
    
    
		printf("data is %5d,the address is 0x%x\n",x->key,x);
	}
}


 
//得到最大值
ST *tree_max(ST *x)
{
    
    
	//最右最下的那个叶子结点就是最大值 
	while(x->right!=NULL)
	{
    
    
		x=x->right;
	}
	return x;
} 



//得到最小值
ST *tree_min(ST *x)
{
    
    
	//最左最下的那个叶子结点就是最小值 
	while(x->left!=NULL)
	{
    
    
		x=x->left;
	}
	return x;
} 



//得到指定结点x的后继结点
//后继结点就是所有大于该结点树节点中最小的那个
ST *tree_successor(ST *x)
{
    
    
	//如果该结点有右子树，那么后继就是右子树的最小值 
	if(x->right!=NULL)
	{
    
    
		return tree_min(x->right);
	}
	ST *y=x->p;
	//如果没有右子树，那么后继结点就是该结点的一个上层结点
	//而且该结点一定是这个上层结点的左子树中的结点
	//那么后继就是第一个满足条件的祖先结点 
	while(y!=NULL&&x==y->right)
	{
    
    
		x=y;
		y=y->p;
	}
	return x; 
}



//得到指定结点x的前驱结点
//前驱结点就是所有小于该结点树节点中最大的那个
ST *tree_precursor(ST *x)
{
    
    
	//如果该结点有左子树，那么前驱就是左子树的最大值 
	if(x->left!=NULL)
	{
    
    
		return tree_max(x->left);
	}
	ST *y=x->p;
	//如果没有左子树，那么前驱结点就是该结点的一个上层结点
	//而且该结点一定是这个上层结点的右子树中的结点
	//那么前驱就是第一个满足条件的祖先结点 
	while(y!=NULL&&x==y->left)
	{
    
    
		x=y;
		y=y->p;
	}
	return x; 
} 



//给树中插入函数
ST *tree_insert(ST *x,int k)
{
    
    
	ST *y=NULL;
	ST *head=x;
	//如果是空结点，那么直接连接 
	if(x==NULL)
	{
    
    
		//动态分配空间 
		y=(ST *)malloc(sizeof(ST));
		y->key=k;
		y->left=NULL;
		y->p=NULL;
		y->right=NULL;
		x=y;
		return x;
	}
	//如果树不为空
	//那么按照搜索树的规则，找到要插入对象的位置
	//该位置是一个叶子结点 
	while(x!=NULL)
	{
    
    
		y=x;
		if(x->key>k)
		{
    
    
			x=x->left;
		}
		else
		{
    
    
			x=x->right;
		}
	}
	//分配空间 
	x=(ST *)malloc(sizeof(ST));
	x->key=k;
	x->p=y;
	x->left=NULL;
	x->right=NULL;
	if(y->key>k)
	{
    
    
		y->left=x;
	}
	else
	{
    
    
		y->right=x;
	}
	return head;
} 



//将一颗子树替换为另一颗子树
void ctree_change(ST *x,ST *u,ST *v)
{
    
    
	if(x==u)
	{
    
    
		x=v;
	}
	else if(u==u->p->left)
	{
    
    
		u->p->left=v;
	}
	else
	{
    
    
		u->p->right=v;
	}
	if(v!=NULL)
	{
    
    
		v->p=u->p;
	}
} 



//删除一个结点
void tree_delet(ST *x,int k)
{
    
    
	ST *k_p;
	k_p=tree_search(x,k);
	if(k_p==NULL)
	{
    
    
		printf("there is no k in tree\n");
	}
	else
	{
    
    
		//如果没有左子树
		//那么直接用右子树替换该子树 
		if(k_p->left==NULL)
		{
    
    
			ctree_change(x,k_p,k_p->right);
			free(k_p);
		}
		//如果没有右子树
		//那么直接用左子树替换该子树
		else if(k_p->right==NULL)
		{
    
    
			ctree_change(x,k_p,k_p->left);
			free(k_p);
		}
		else
		{
    
    
			ST *temp=NULL;
			//找到后继结点 
			temp=tree_min(k_p->right);
			if(temp->p!=k_p)
			{
    
    
				//将后继结点提取出来 
				ctree_change(x,temp,temp->right);
				//将后继结点与被删除结点的右子树相连 
				temp->right=k_p->right;
				temp->right->p=temp;
			}
			//提取被删除结点 
			ctree_change(x,k_p,temp);
			//将后继结点与被删除结点的左子树连接 
			temp->left=k_p->left;
			temp->left->p=temp;
			free(k_p);
		}
	}
} 



//主测试函数 
int main()
{
    
    
	ST *t=NULL;//搜索二叉树 
	ST *temp;//中间存储结点 
	int a[SIZE];
	int i=0;
	//生成原始随机数据 
	srand((unsigned)time(NULL));
	for(i=0;i<SIZE;i++)
	{
    
    
		a[i]=rand()%LIM;
	}
	//打印原始数据
	for(i=0;i<SIZE;i++)
	{
    
    
		printf("%5d",a[i]);
	}
	printf("\n"); 
	//生成搜索二叉树
	for(i=0;i<SIZE;i++)
	{
    
    
		t=tree_insert(t,a[i]);
	}
	//用中序遍历打印生成的搜索二叉树
	//结果是排好序的，从小到大 
	print_tree(t); 
	//查找值
	//存在的值 
	temp=tree_search(t,a[5]);
	print_search(temp);
	//不存在的值 
	temp=tree_search(t,LIM);
	print_search(temp);  
	//返回最大值，最小值
	//最小值 
	temp=tree_min(t);
	printf("min is %5d\n",temp->key);
	//最大值 
	temp=tree_max(t);
	printf("max is %5d\n",temp->key);
	//返回前驱值和后继
	//前驱值
	temp=tree_precursor(t);
	printf("the precursor of root data %5d is %5d\n",t->key,temp->key);
	//后继值 
	temp=tree_successor(t);
	printf("the successor of root data %5d is %5d\n",t->key,temp->key);
	//删除值
	tree_delet(t,a[5]);
	print_tree(t); 
	return 0;
} 

---

总结

本文的不妥之处请读者包涵指正