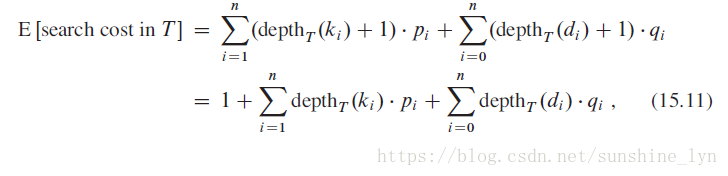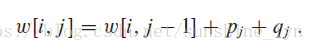《算法导论》之最优二叉搜索树

最优二叉搜索树

假定我们正在设计一个程序，实现英语文本到法语的翻译。对英语文本中出现的每个单词，我们需要查找对应的法语单词。为了实现这些查找操作，可以创建一棵二叉搜索树，将n个英语单词作为关键字，对应的法语单词作为关联数据。由于文本中的每个单词都要进行搜索，我们希望花费在搜索上的总时间尽量少。

通过红黑树或其他平衡搜索树结构，我们可以假定每次搜索时间为O(lgn) 。但由于单词出现的频率是不同的，像“the”这种频繁使用的单词有可能位于搜索树中远离根的位置上，而像“machicolation”这种很少使用的单词可能位于靠近根的位置上。这样的结构会减慢翻译的速度，因为二叉树搜索树中搜索一个关键字的权重是深度+1。我们希望文本中频繁出现的单词被置于靠近根的位置。在给定单词出现频率的前提下，我们应该如何组织一棵二叉搜索树，使得所有搜索操作访问的结点总数最少呢？

---

这个问题称为最优二叉搜索树(optimal binary search tree)问题。其形式化定义如下：给定一个n个不同关键字已排序的序列 $K=<k1,k2,...,kn>$ (因此 $k1<k2<...<kn$ )，我们希望用这些关键字构造一棵二叉搜索树。对每个关键字 $ki$ ，都有一个概率pi表示其搜索频率。有些要搜索的值可能不在 $K$ 中，因此我们还有 $n+1$ 个“伪关键字” $d0,d1,d2...dn$ 表示不在K中的值。 $d0$ 表示所有小于 $k1$ 的值， $dn$ 表示所有大于 $kn$ 的值，对 $i=1,2,...,n-1$ ，伪关键字di表示所有在 $ki$ 和 $ki+1$ 之间的值。对每个伪关键字 $di$ ，也都有一个概率 $pi$ 表示对应的搜索频率。

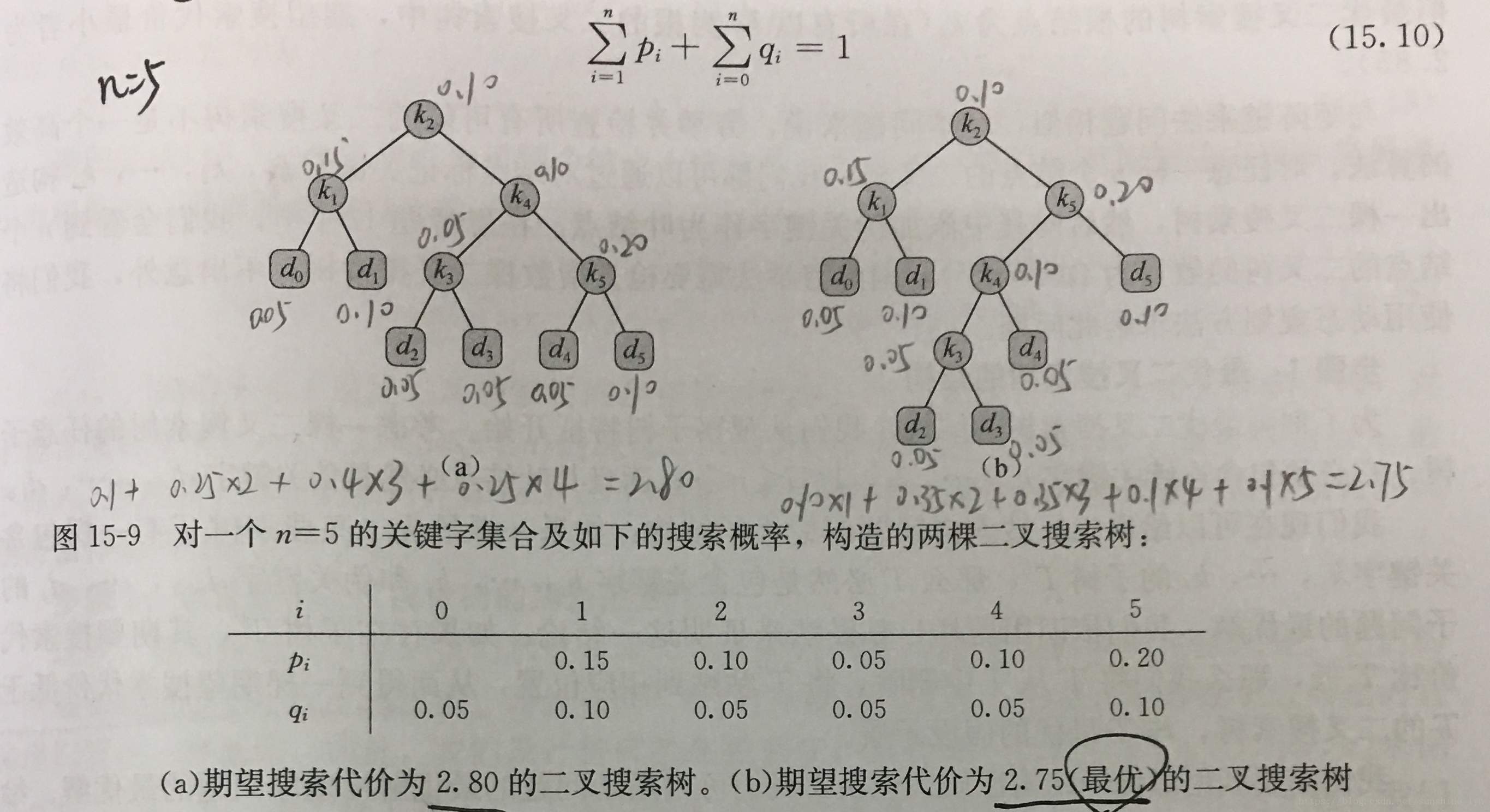
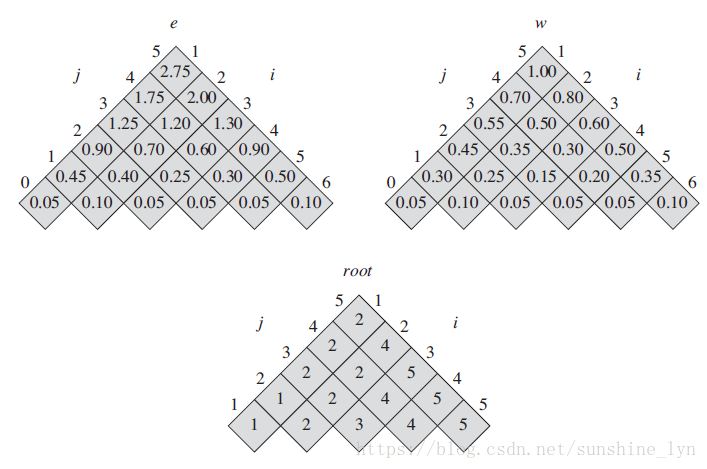
下图显示了对一个n=5个关键字的集合构造的两颗二叉搜索树。每个关键字 $ki$ 是一个内部结点，而每个伪关键字 $di$ 是一个叶结点。每次搜索要么成功(找到某个关键字 $ki$ )要么失败(找到某个伪关键字 $di$ )，因此有如下公式：

由于我们知道每个关键字和伪关键字的搜索频率，因而可以确定在一棵给定的二叉搜索树 $T$ 中进行一次搜索的期望代价。假定一次搜索的代价等于访问的结点数，即此次搜索找到的结点在 $T$ 中的深度再加 $1$。那么在 $T$中进行依次搜索的期望代价为：

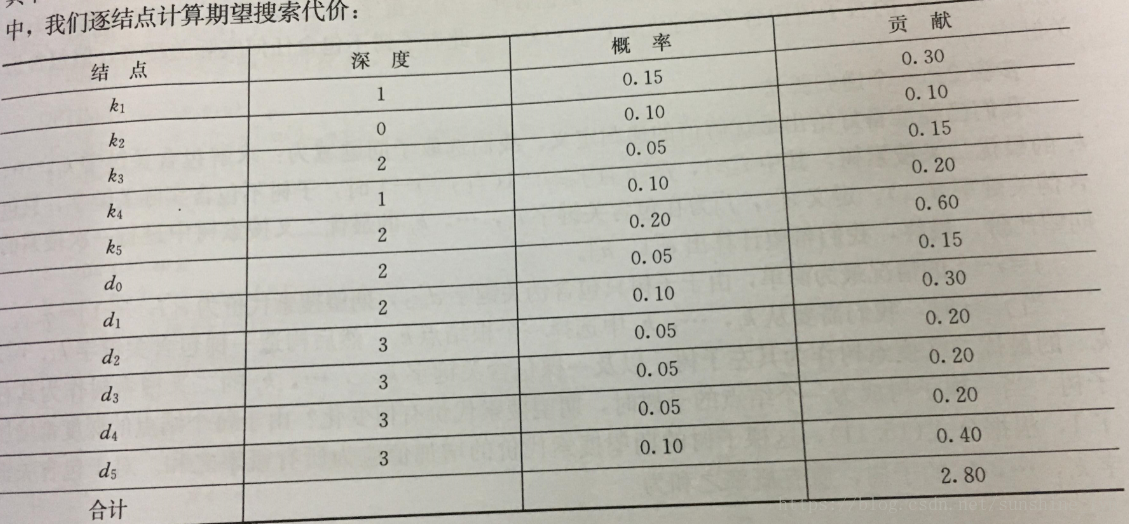
其中 $depth(T)$ 表示一个结点在树T中的深度。最后一个等式是由公式(15.10)推导而来。在图15-9(a)中，我们逐结点计算期望搜索代价：

对于一个给定的概率集合，我们希望构造一棵期望搜索代价最小的二叉搜索树，我们称之为最优二叉搜索树。图15-9(b)所示的二叉搜索树就是给定概率集合的最优二叉搜索树，其期望代价为2.75。这个例子显示二叉搜索树不一定是高度最矮的。而且，概率最高的关键字也不一定出现在二叉树搜索树的根结点。在此例中，关键字 $k5$ 的搜索概率最高，但最优二叉搜索树的根结点为 $k2$ (在所有以 $k5$ 为根的二叉搜索树中，期望搜索代价最小者为2.85)。

与矩阵链乘法问题相似，对本问题来说，采用穷举法需检查指数棵二叉搜索树。不出意外，将使用动态规划方法求解此问题。

• 步骤1：最优二叉搜索树的结构
  为了刻画最优二叉搜索树的结构，我们从观察子树特征开始。考虑一棵二叉搜索树的任意子树。它必须包含连续关键字 $k(i),...k(j)，1<=i<=j<=n，$ 而且其叶结点必然是伪关键字 $d(i-1),...,d(j)$ 。

  我们现在可以给出二叉搜索树问题的最优子结构：如果一棵最优二叉搜索树T有一棵包含关键字 $k(i),...,k(j)$ 的子树T’，那么T’必然是包含关键字 $k(i),...,k(j)$ 和伪关键字 $d(i-1),...,d(j)$ 的子问题的最优解。我们依旧用“剪切-粘贴”法来证明这一结论。如果存在子树T’’，其期望搜索代价比T’低，那么我们将T’从T中删除，将T’'粘贴到相应的位置，从而得到一颗期望搜索代价低于T的二叉搜索树，与T最优的假设矛盾。

  我们需要利用最优子结构性质来证明，我们可以用子问题的最优解构造原问题的最优解。给定关键字序列 $k(i),...,k(j)$，其中某个关键字，比如说 $k(r)(i<=r<=j)$，是这些关键字的最优子树的根结点。那么k®的左子树就包含关键字 $k(i),...,k(r-1)$(和伪关键字 $d(i-1),...,d(r-1)$)，而右子树包含关键字 $k(r+1),...,k(j)$(和伪关键字 $d(r),...,d(j)$)。只要我们检查所有可能的根结点 $k(r)(i<=r<=j)$，并对每种情况分别求解包含 $k(i),...,k(r-1)$及包含 $k(r+1),...,k(j)$的最优二叉搜索树，即可保存找到原问题的最优解。

  这里还有一个值得注意的细节——“空子树”。假定对于包含关键字 $ki,...,kj$的子问题，我们选定 $ki$为根结点。根据前文论证， $k(i)$的左子树包含关键字 $k(i),...,k(i-1)$的子问题，我们将此序列解释为不包含任何关键字。但请注意，子树仍然包含伪关键字。按照惯例，我们认为包含关键字序列 $k(i),...,k(i-1)$的子树不包含任何实际关键字，但包含单一伪关键字 $d(i-1)$。对称地，我们如果现在 $k(j)$为根结点，那么 $k(j)$的右子树包含关键字 $k(j+1),...,k(j)$——此右子树不包含任何实际关键字，但包含伪关键字 $d(j)$。

• 步骤2：一个递归算法

  我们已经准备好给出最优解值的递归定义。我们选取子问题域为：求解包含关键字 $k(i),...,k(j)$的最优二叉搜索树，其中 $i>=1，j<=n$且 $j>=i-1$(当 $j=i-1$时，子树不包含实际关键字，只包含伪关键字 $d(i-1)$。定义 $e[i,j]$为包含关键字 $k(i),...,k(j)$的最优二叉搜索树中进行一次搜索的期望代价，最终，我们希望计算出 $e[1,n]$。

  j=i-1的情况最为简单，由于子树只包含伪关键字d(i-1)，期望搜索代价为 $e[i,i-1]=q(i-1)$ 。

  当 $j>=i$时，我们需要从 $k(i),...,k(j)$中选择一个跟结点 $k(r)$，然后构造一棵包含关键字 $k(i),...,k(r-1)$的最优二叉搜索树作为其左子树，以及一棵包含关键字 $k(r+1),...,k(j)$的二叉搜索树作为其右子树。当一棵子树成为一个结点的子树时，期望搜索代价有何变化？由于每个结点的深度都增加了1，根据公式(15.11)，这棵子树的期望搜索代价的增加值应为所有概率这和。对于包含关键字 $k(i),...,k(j)$ 的子树，所有概率之和为：
  

  因此，若k为包含关键字 $k(i),...,k(j)$ 的最优二叉搜索树的根结点，我们有如下公式：
  $e[ i , j ] =p ( r ) + (e[ i , r-1 ] + w( i , r-1 ) ) + ( e[ r+1 , j ] + w( r+1 , j ) )$
  注意， $w( i , j ) = w( i , r-1 ) + p ( r ) + w( r + 1 , j )$
  因此e[ i , j ]可重写为：
  $e[ i , j ] = e[ i , r-1 ] + e[ r+1 , j ] + w( i , j )$ (15.13)
  递归公式(15.13)假定我们知道哪个结点k应该作为根结点。如果选取期望搜索代价最低者作为根结点，可得最终递归公式(15.14)：
  ①若j=i-1， $e[i,j]=q(i-1)$
  ②若i<=j， $e[i,j]=min{e[i,r-1]+e[r+1,j]+w(i,j)} (i&lt;=r&lt;=j)$
  $e[i,j]$ 的值给出了最优二叉搜索树的期望搜索代价。为了记录最优二叉搜索树的结构，对于包含关键字 $k(i),...,k(j)(1&lt;=i&lt;=j&lt;=n)$ 的最优二叉搜索树，我们定义 $root[i,j]$ 保存根结点 $k(r)$ 的下标r。

• 步骤3：计算最优二叉搜索树的期望搜索代价

  现在，我们可以注意到我们求解最优二叉搜索树和矩阵链乘法的一些相似之处。它们的子问题都由连续的下标子域组成。而公式(15.14)的直接递归实现，也会与矩阵链乘法问题的直接递归算法一样低效。因此，我们设计替代的高效算法，我们用一个表 $e[1..n+1,0..n]$来保存 $e[ i , j ]$的值。第一维下标上界为 $n+1$ 而不是 $n$，原因在于对于只包含伪关键字d(n)的子树，我们需要计算并保存 $e[n+1,n]$。第二维下标下界为 $0$，是因为对于只包含伪关键字 $d0$的子树，我们需要计算并保存 $e[1,0]$。我们只使用表中满足 $j&gt;=i-1$的表项 $e[i,j]$。我们还使用一个表root记录关键字 $ki,...kj$的子树的根。我们只使用此表中满足 $1&lt;=i&lt;=j&lt;=n$的表项 $root[i,j]$;

  我们还需要另一个表来提高计算效率。为了避免每次计算 $e[i,j]$时都重新计算 $w(i,j)$，我们将这些值保存在表 $w[1..n+1,0..n]$中，这样每次可节省 $Θ(j-i)$次加法。对基本情况，令 $w[i,i-1]=q(i-1)(1&lt;=i&lt;=n+1)$。对 $j&gt;=i$ 的情况，可如下计算：
  $w[i,j]=w[i,j-1]+p(j)+q(j)$ (15.15)
  这样对 $Θ(n^2)$个 $w[i,j]$，每个计算时间为 $Θ(1)$。下面的代码接受概率列表 $p$和 $q$及规模 $n$作为输入，返回表 $e$和 $root$。

下图给出了OPTIMAL_BST输入图15-9中的关键字分布后计算出的表 $e[i,j]、w[i,j]和root[i,j]$。类似于矩阵链乘法问题的输出结构，也是对表进行了旋转。按自底向上的顺序逐行计算，在每行中由左至右计算每个表项。

时间复杂度为 $Θ（n^3）$。 由于它包含三重for循环，而每层循环的下标最多取 $n$个值，因此很容易得出其运行时间为 $O(n^3)$。

---

参考资料：
[1].《算法导论》第三版