题目链接:
难度二:P4779 【模板】单源最短路径(标准版) (慎入)
题目简述: 给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
输入格式: 第一行包含三个整数N、M、S,分别表示点的个数、有向边的个数、出发点的编号。
接下来M行每行包含三个整数Fi、Gi、Wi,分别表示第i条有向边的出发点、目标点和长度。
输出格式 :仅一行,包含N个用空格分隔的整数,其中第i个整数表示从点S出发到点i的最短路径长度(若S=i则最短路径长度为0,若从点S无法到达点i,则最短路径长度为2147483647)
样例数据
输入:
4 6 1
1 2 2 2 3 2 2 4 1 1 3 5 3 4 3 1 4 4
输出:
0 2 4 3
常见的图论解法有4种(⊙o⊙)哦
第一种:Floyd算法
思想:
Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题,我们需要为这个目标重新做一个诠释(这个诠释正是动态规划最富创造力的精华所在)
从任意节点i到任意节点j的最短路径不外乎2种可能,一是直接从i到j;二是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
优点:
容易理解,可以算出任意两个节点之间的最短距离,代码编写简单。并可以处理负边权问题
缺点:
时间复杂度比较高,不适合计算大量数据。时间复杂度O(n^3),空间复杂度O(n^2)。且不能处理负环回路问题
初始化&&输入:
Floyd常用邻接矩阵(二维数组)来存储;即F[i][j]存储从点 i 到点 j 的距离dis
值得一提的是:在初始化时,要将所有的点存为+∞,表示从点 i 到点 j 无法到达,再将F[i][j]赋值为 0(i==j)
所有的 Dis[i]=MAXN;Dis[S]=0;//详见下楼代码
代码实现:
1 for(L k=1; k<=N; ++k)//枚举中间点
2 for(L i=1; i<=N; ++i )//枚举起点 3 for(L j=1; j<=N; ++j)//枚举终点 4 if(F[i][j]+ANS[i]<ANS[j]) //若经过中间点的距离小于已知最短的距离!!! 5 ANS[j]=F[i][j]+ANS[i];//更新数据
完整代码:
1 //Floyd版
2 #include<algorithm>
3 #include<cstdio>
4 #include<cstdlib> 5 #include<cstring> 6 #include<iostream> 7 using namespace std; 8 typedef long long L; 9 const L MAXN=2147483647; 10 L F[10010][10010],ANS[10010]; 11 inline L read()//快速读入,PS:可以直接用scanf,此次是笔者打习惯了 12 { 13 L w=0,x=0; 14 char ch=0; 15 while(!isdigit(ch))w|=ch=='-',ch=getchar(); 16 while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); 17 return w?-x:x; 18 } 19 int main(void) 20 { 21 L N=read(),M=read(),S=read(); 22 for(L i=1; i<=N; ++i)//初始化 23 { 24 for(L j=1; j<=N; ++j) F[i][j]=(i==j?0:MAXN); 25 ANS[i]=MAXN; 26 } 27 for(L i=1; i<=M; ++i)//输入 28 { 29 L A=read(),B=read(),l=read(); 30 F[A][B]=min(F[A][B],l); 31 } 32 ANS[S]=0,F[1][1]=0; 33 for(L k=1; k<=N; ++k)//Floyd算法实现 34 for(L i=1; i<=N; ++i ) 35 for(L j=1; j<=N; ++j) 36 if(F[i][j]+ANS[i]<ANS[j]) 37 ANS[j]=F[i][j]+ANS[i]; 38 for(L i=1; i<=N; ++i) printf("%lld ",ANS[i]);//输出 39 return 0; 40 } 41
评价:
这种算法虽然时间复杂度较高,但胜在容易理解,并且代码简便,清晰。在其他算法不会时可以骗个30分。(⊙o⊙)嗯!!!
第二种:Dijkstra算法
基本思想:
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
算法步骤:
1.初始时, From 只包含源点,即 From={S} 。 U 包含除 S 外的其他顶点,即:U={其余顶点}。 f 为 From 内一点, u 为 U 内一点。若从 f 能到 u 则 MAP[i] 。[j]!=MAXN,若f不能到 u ,则 MAP[i][j] 权值为 MAXN 。
2.从 U 中选取一个距离 S 最小的顶点 f ,把 f ,加入 From 中(该选定的距离就是 S 到 f 的最短路径长度)。
3.以 f 为新考虑的中间点,修改 U 中各顶点的距离:若从起点 S 到顶点 u 的距离(经过顶点 f )比原来距离(不经过顶点 f )短,则修改顶点 u 的距离值,修改后的距离值的顶点 f 的距离加上边上的权。
4.重复步骤 2 和 3 直到所有顶点都包含在 From 中。
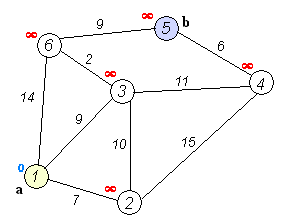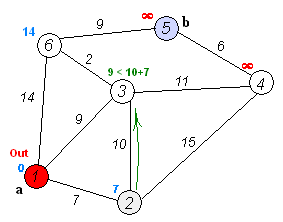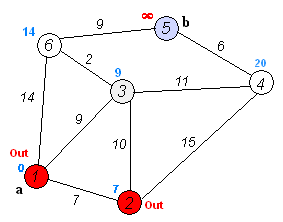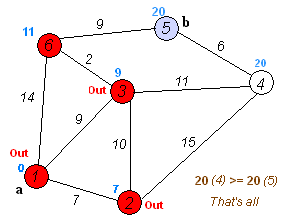
未优化版:
1.邻接矩阵存储:
//Dijkstra版(未优化)
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring> #include<iostream> using namespace std; typedef long long L; const L MAXN=2147483647; L MAP[10010][10010],Dis[10010]; bool from[10010]; inline L read() //快读 { L w=0,x=0; char ch=0; while(!isdigit(ch))w|=ch=='-',ch=getchar(); while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); return w?-x:x; } int main(void) { L N=read(),M=read(),S=read(); for(L i=1; i<=N; ++i)//初始化 { for(L j=1; j<=N; ++j) MAP[i][j]=(i==j?0:MAXN); Dis[i]=(i==S)?0:MAXN; } for(L i=1; i<=M; ++i) //输入 { L f=read(),to=read(),dis=read(); MAP[f][to]=min(W,MAP[F][G]); } for(L i=1; i<N; ++i)//共有N个顶点,除终点外还有N-1 个顶点 { L MINN=MAXN,f=0; for(L j=1; j<=N; ++j) //查找从S到u的最短路 if( (!from[j] ) && (Dis[j]<MINN) )//(!from[j])因为必须是从U中取出的顶点 MINN=Dis[j],f=j; from[f]=true;//记录这点已在From中 for(L j=1; j<=N; ++j) Dis[j]=(Dis[f]+MAP[f][j]<Dis[j])?Dis[f]+MAP[f][j]:Dis[j];//更新数据 } for(L i=1; i<=N; ++i) printf("%lld ",Dis[i]);//输出 return 0; }
2.邻接表存储(前向星):(前向星的会比较难懂一点,大家尽量看看嘛。毕竟后面的堆优化是要用到的,而且光一个前向星就能少很多空间了)
1 #include<algorithm>
2 #include<cstdio>
3 #include<cstdlib>
4 #include<cstring>
5 #include<iostream>
6 using namespace std; 7 typedef long long L; 8 const L MAXN=2147483647; 9 struct Edge//前向星 10 { 11 L next;//下一条边的编号 12 L to;//这条边到达的点 13 L dis;//这条边的长度 14 } E[500010]; 15 L num_edge=0,Head[10010],Dis[10010]; 16 bool from[10010]; 17 inline L read() //快读 18 { 19 L w=0,x=0; 20 char ch=0; 21 while(!isdigit(ch))w|=ch=='-',ch=getchar(); 22 while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); 23 return w?-x:x; 24 } 25 inline void Add_edge(L from,L to,L d)//前向星插入 26 { 27 ++num_edge; 28 E[num_edge].next=Head[from]; 29 E[num_edge].to=to; 30 E[num_edge].dis=d; 31 Head[from]=num_edge; 32 } 33 int main(void) 34 { 35 L N=read(),M=read(),S=read(); 36 for(int i=1; i<=N; ++i) Dis[i]=(i==S)?0:MAXN;//初始化 37 for(L i=1; i<=M; ++i)//输入 38 { 39 L u=read(),v=read(),d=read(); 40 Add_edge(u,v,d); 41 } 42 L f=S; 43 while(!from[f]) 44 { 45 from[f]=true; 46 47 for(L i=Head[f]; i!=0; i=E[i].next)//修改点距离 48 if( !from[E[i].to ] && (Dis[f]+E[i].dis<Dis[E[i].to]) ) 49 Dis[E[i].to]=Dis[f]+E[i].dis;//更新 50 51 L MINN=MAXN; 52 for(L i=1; i<=N; ++i)//寻找最小点 53 { 54 55 if(!from[i]&&Dis[i]<MINN) 56 { 57 MINN=Dis[i]; 58 f=i; 59 } 60 } 61 } 62 for(L i=1; i<=N; i++)printf("%lld ",Dis[i]);//输出 63 return 0; 64 }
堆优化版:
其中的 pair 参见: C++ std::pair的用法
priority_queue优先队列参见:STL--priority_queue用法
堆优化的原理网上大佬们都讲得不大好,本弱鸡也讲不清,个人建议是背下来。の平时一些不会的大难题也是这么干的。O(∩_∩)O~
1 //Dijkstra版(堆优化)
2 #include<algorithm>
3 #include<cstdio>
4 #include<cstdlib> 5 #include<cstring> 6 #include<iostream> 7 #include<queue> 8 #include<vector> 9 using namespace std; 10 typedef long long L; 11 typedef pair<L,L> node; 12 const L MAXN=2147483647;//最大值 13 struct Edge 14 { 15 L next;//下一条边的编号 16 L to;//这条边到达的点 17 L dis;//这条边的长度 18 } E[500010]; 19 L num_edge=0,Head[10010],Dis[10010],N,M,S; 20 bool Map[10010]; 21 inline L read() //快读 22 { 23 L w=0,x=0; 24 char ch=0; 25 while(!isdigit(ch))w|=ch=='-',ch=getchar(); 26 while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); 27 return w?-x:x; 28 } 29 inline void Add_edge(L from,L to,L d)//前向星存储试插入 30 { 31 ++num_edge; 32 E[num_edge].next=Head[from]; 33 E[num_edge].to=to; 34 E[num_edge].dis=d; 35 Head[from]=num_edge; 36 } 37 inline void Scanf()//输入与初始化 38 { 39 N=read(); 40 L M=read(),S=read(); 41 for(int i=1; i<=N; ++i) Dis[i]=(i==S)?0:MAXN; 42 for(L i=1; i<=M; ++i) 43 { 44 L u=read(),v=read(),d=read(); 45 Add_edge(u,v,d); 46 } 47 } 48 inline void Printf()//输出答案 49 { 50 for(L i=1; i<=N; i++)printf("%lld ",Dis[i]); 51 52 } 53 inline void Dijkstra()//Dijkstra 算法实现 54 { 55 priority_queue< node,vector<node>,greater<node> > T;//小根堆 56 57 T.push(make_pair(0,S)); 58 59 while(!T.empty()) 60 { 61 L f=T.top().second; 62 T.pop(); 63 for(L i=Head[f]; i!=0; i=E[i].next) 64 { 65 if(Dis[f]+E[i].dis<Dis[E[i].to]) 66 { 67 Dis[E[i].to]=Dis[f]+E[i].dis; 68 T.push(make_pair(Dis[E[i].to],E[i].to)); 69 } 70 } 71 } 72 } 73 int main(void) 74 { 75 Scanf(); 76 Dijkstra(); 77 Printf(); 78 return 0; 79 }