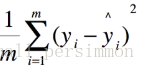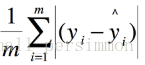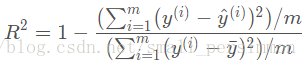算法学习——线性回归

1.线性回归模型表示

一元线性回归表示： $y(x,w) = w_{0} + w_{1}x$

多元线性回归表示： $y(x,w) = w_{0} + w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{n}x_{n}$

矩阵表示： $y(x,w) = W^{T}X$ ，其中

$W = \begin{bmatrix} w_{0}\\ w_{1}\\ w_{2}\\ \cdots\\ w_{n} \end{bmatrix}$ $X = \begin{bmatrix} 1\\ x_{1}\\ x_{2}\\ \cdots\\ x_{n}\\ \end{bmatrix}$

2.目标函数——平方损失函数

一个数据点为 $(x_{i},y_{i})$ 的误差：

$y_{i} - (\theta _{0} + \theta _{1}x_{i})$

误差损失总和——残差：

$\sum _{i=1}^{n}(y_{i} - (\theta _{0} + \theta _{1}x_{i}))$

使用残差的平方和（RSS）或最小化均方误差（MSE）来表示所有样本点的误差「平方损失函数」：

$J(\theta) = \sum _{i=1}^{n}(y_{i} - (\theta _{0} + \theta _{1}x_{i}))^2{}$

3.最小二乘的概率解释

4.最小二乘解法一——梯度下降

梯度下降是一个需要进行迭代的，求局部最小值的算法，下面给出迭代规则：

把 $J(\theta)$ 带入并求 $\theta_{j}$ 的偏导数即可得到更新规则，:= 在这里表示赋值，当只有一个样本的时候，更新规则如下：

带入（11），得到：

每做一次求导都表示找到了当前位置梯度最陡的方向， $\alpha$ 代表学习速率，即步长。

下面提供三种具体的实施方式：

批量梯度下降（BGD）

批梯度下降一次迭代会更新所有θ，每次更新都是向着最陡的方向前进。每一次迭代都需要把所有的样本（共m个）取到，把每一个样本的真实值减去预测值，再把这个差值乘上该样本的第i个特征。重复迭代p次之后收敛了（当两次迭代的值几乎不发生变化时，可判断收敛），然后又重复如上步骤获得θ1、θ2、……θn，最后取得最终的参数向量θ，去画出我们的预测直线。

优点：得到全局最优解，易于并行实现

缺点：当样本数目很多时，训练过程会很慢

随机梯度下降（SGD）

随机梯度下降法为最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向，但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。也就是说我用样本中的一个例子来近似我所有的样本，来调整θ，其不会计算斜率最大的方向，而是每次只选择一个维度踏出一步；下降一次迭代只更新某个θ，抱着并不严谨的走走看的态度前进。

优点：训练速度快

缺点：准确度下降，并不是全局最优，不易与并行实现

小批量梯度下降（MBGD）

MBGD是一种介于SGD和BGD两种方法之间的一种折中的梯度下降法：在每一步中，不是基于完整训练集（如BGD）或仅基于一个实例（如SGD中那样）计算梯度，而是在小随机实例集上的梯度。

5.最小二乘解法二——正规方程组

$J(\theta)$ 可以通过直接求出最小值点，在最小值点， $J(\theta)$ 各个方向的偏导均为零。

常用向量矩阵求导公式

6.评价指标

均方误差（MSE）

均方根误差（RMSE）

平均绝对误差（MAE）

R-Squared

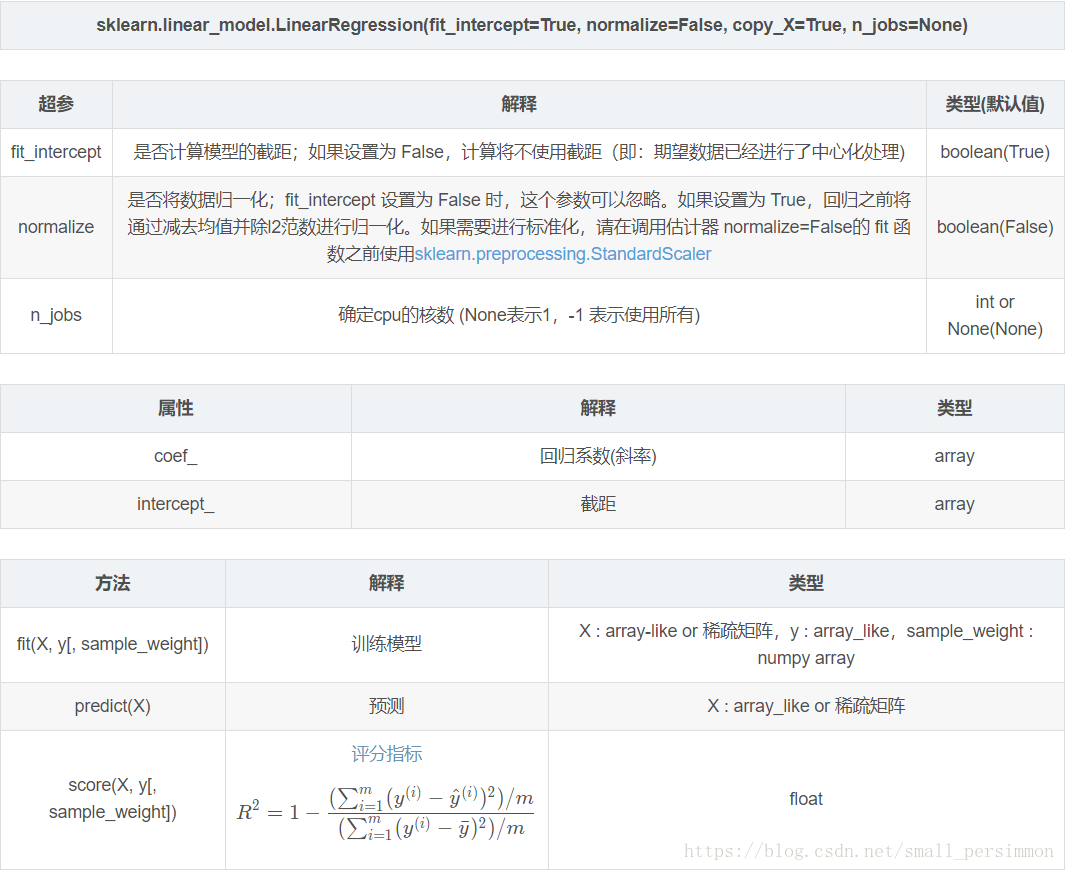
7.算法实现

参数解释：

调包实践：

    import matplotlib.pyplot as plt
    import numpy as np
    from sklearn import datasets, linear_model
    from sklearn.metrics import mean_squared_error, r2_score

    experiences = np.array([0,1,2,3,4,5,6,7,8,9,10])
    salaries = np.array([103100, 104900, 106800, 108700, 110400, 112300, 114200, 116100,      117800, 119700, 121600])

    # 将特征数据集分为训练集和测试集，除了最后5个作为测试用例，其他都用于训练
    X_train = experiences[:7]
    X_train = X_train.reshape(-1,1)
    X_test = experiences[7:]
    X_test = X_test.reshape(-1,1)

    # 把目标数据（特征对应的真实值）也分为训练集和测试集
    y_train = salaries[:7]
    y_test = salaries[7:]

    # 创建线性回归模型
    regr = linear_model.LinearRegression()

    # 用训练集训练模型——看就这么简单，一行搞定训练过程
    regr.fit(X_train, y_train)

    # 用训练得出的模型进行预测
    diabetes_y_pred = regr.predict(X_test)

    # 将测试结果以图标的方式显示出来
    plt.scatter(X_test, y_test,  color='black')
    plt.plot(X_test, diabetes_y_pred, color='blue', linewidth=3)

    plt.xticks(())
    plt.yticks(())

    plt.show()

参考链接：

线性回归、逻辑回归、广义线性模型——斯坦福CS229机器学习个人总结（一）

线性回归——爖

回归评价指标MSE、RMSE、MAE、R-Squared

线性回归算法——黑桃

算法实践1_线性回归——Datawhale