关于稀疏

稀疏编码 Sparse Coding 与字典学习

定义变量：

样本集用Y表示（M×N），M表示样本数，N表示样本属性个数
字典矩阵用D表示（M×K）
稀疏矩阵用X表示（K×N）

第 i 个原始数据 Yi 的稀疏表示 Xi 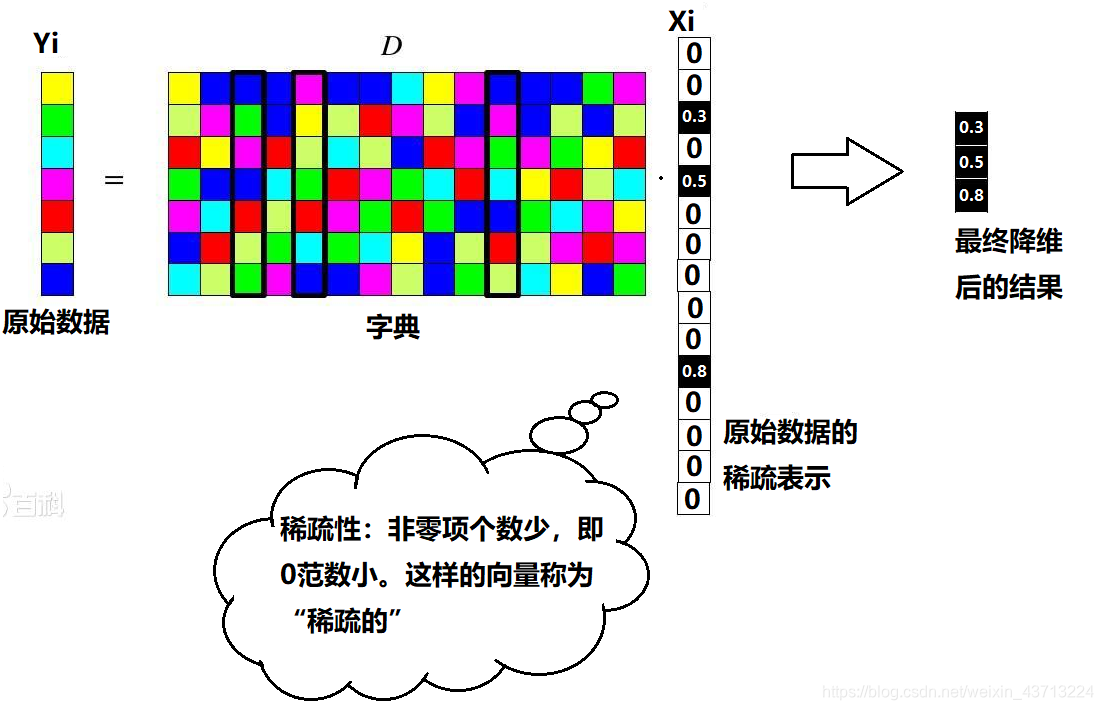：在这里插入图片描述

南大周志华老师写的《机器学习》这本书上原文：“为普通稠密表达的样本找到合适的字典，将样本转化为合适的稀疏表达形式，从而使学习任务得以简化，模型复杂度得以降低，通常称为‘字典学习’（dictionary
learning），亦称‘稀疏编码’（sparse coding）”块内容。

为了求出D，需要求解以下优化问题：
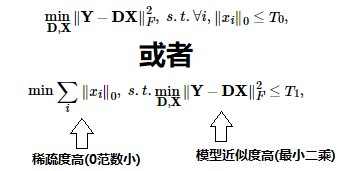
在这里插入图片描述
求解方法通常用 K-SVD ，具体过程见参考文献：字典学习和K-SVD

神经网络的正则化 / 稀疏化

神经网络的稀疏性实际上指的是权重的稀疏性，控制稀疏性的方法有两个：

方法1：在损失函数上加入正则项（又称为稀疏性限制），保证稀疏性，实现控制网络的稀疏程度。
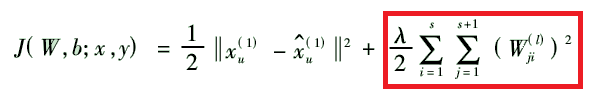
方法2：选合适的激活函数（例如梯度很大的sigmoid函数）也可以使节点的值偏向0和1两个极端，使得网络稀疏性增大
方法3：采用 DROP-OUT 抛弃部分神经元，相当于强制置0

正则化则化的好处（待补充）主要有：

从数学上解释：网络参数“非零即1”，意味着线性映射中 W 近似于一组 “正交基向量”（又称为正则基）。如果网络参数不稀疏，则显然基向量之间相关性强，正交性弱。（待补充）
从经验上解释：人脑神经通常也处于激活、非激活的0、1状态，这样可以提高工作效率。网络参数正则化可以提高训练效率、减小过拟合，提高泛用性。

应注意：正则化和稀疏化、稀疏学习实际上是同一概念！稀疏学习的意义待补充。

深度学习稀疏自编码网络

自编码 Autoencoder：对三层网络，令输入=输出、隐层节点数<输入层节点数，训练完成后将隐层作为数据的低维表示
稀疏自编码 Sparse Autoencoder：当隐层节点数>输入层节点数时，可以对神经网络加入稀疏性限制（例如使用上面的两种方法），有可能发现输入数据的有趣结构，具体见参考文献

稀疏编码最初的目的是为了稀疏，这样特征更容易线性可分
自编码最初是为了让输出模拟出输入，自编码最重要的是他的副产物，帮助还原输入的隐含层编码, 我们可以利用这层编码做降维或是特征学习
稀疏自编码是其中的一种，加入了保证编码稀疏性的正则项

传统特征降维方法

PCA：使投影后的数据方差最大，属于无监督方法
LDA：使投影后样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性，属于有监督方法
SVD：PCA算法中用到了SVD，类似PCA，可以看成一类（后文中有详细解释）
拉普拉斯图方法：拉普拉斯特征映射将处于流形上的数据，在尽量保留原数据间相似度的情况下，映射到低维下表示，属于无监督方法
深度学习稀疏自编码：对三层网络，令输入=输出、隐层节点数<输入层节点数，训练完成后将隐层作为数据的低维表示，属于无监督方法
稀疏编码最初的目的是为了稀疏，这样特征更容易线性可分
自编码最初是为了让输出模拟出输入，自编码最重要的是他的副产物，帮助还原输入的隐含层编码, 我们可以利用这层编码做降维或是特征学习
稀疏自编码是其中的一种，加入了保证编码稀疏性的正则项
还有 LASSO、流形学习、LLE局部线性嵌入、Isomap等距映射、MDS 等无监督方法
小波分析、傅里叶变换等：有一些变换的操作降低干扰，可以看做是降维

主成分分析法 PCA

在这里插入图片描述

奇异值分解 SVD

在这里插入图片描述

PCA和SVD的关系

不难发现，PCA 中的特征矩阵 V 也是 SVD 中的右正交矩阵 V。PCA中将X投影到第k主成分方向相当于 X·Vk，那么
在这里插入图片描述
因此二者关系是：PCA 是将 SVD 的右正交矩阵作为主成分进行投影。

以下为引用：现在来看一下SVD和PCA的关系。
我们讲到要用PCA降维，需要找到样本协方差矩阵X˜TX˜X_TX的最大的k个特征向量，然后用这最大的k个特征向量张成的矩阵来做低维投影降维。
注意，SVD也可以得到协方差矩阵X˜TX˜X_TX最大的k个特征向量张成的矩阵。
但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵，也能求出右奇异矩阵VV。也就是说，PCA算法可以不用做特征分解，而是做SVD来完成。这也是为什么很多工具包中PCA算法的背后真正的实现是用的SVD，而不是我们认为的暴力特征分解。
另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵。而左奇异矩阵可以用于行数的压缩，右奇异矩阵可以用于列数，也就是PCA降维。所以，有了SVD就可以得到两个方向的PCA。
原文链接：https://blog.csdn.net/qq_24464989/article/details/79834564

稀疏学习、稀疏表示、稀疏自编码神经网络、字典学习、主成分分析PCA、奇异值分解SVD 等概念的梳理，以及常用的特征降维方法