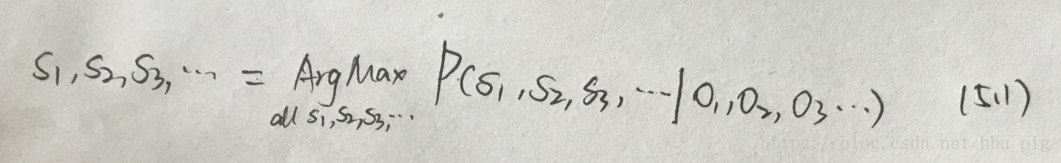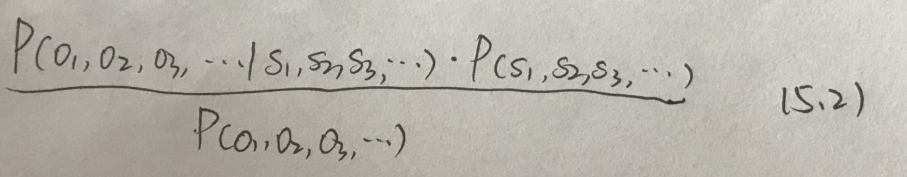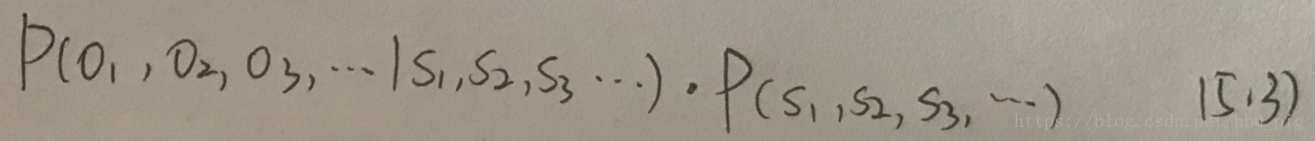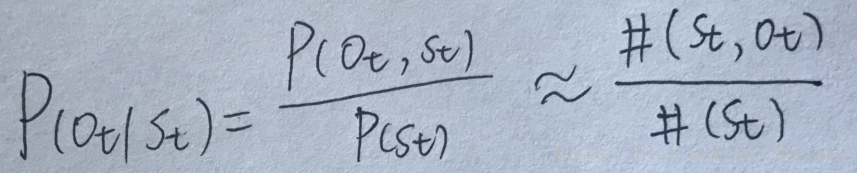隐含马尔可夫模型常用于解决自然语言处理的问题。例如语音识别、机器翻译等。
目录
通信模型
在通信模型中,如何根据观察数据o1,o2,o3,...来推测信号源发送的信息s1,s2,s3,...呢?用概率论的语言来表述,就是求在已知o1,o2,o3,...的情况下s1,s2,s3,...的最大概率,即
根据P(A|B)*P(B)=P(B|A)*P(A),上式右侧等价于

在求最大值的时候,分母P(o1,o2,o3,...)是一个可忽略的常数,等价于求5.2式的分子的最大值。
哈哈,变成这个形式还是不会求解呢?啦啦啦告诉你,这个公式完全可以用隐含马尔可夫模型(Hidden Markov Model)来估计哇。
隐含马尔可夫模型
介绍马尔可夫模型,还是要从马尔可夫链说起。19世纪的时候,概率论的发展从研究随机变量转变为随机过程。随机过程比随机变量要复杂一丢丢。假设有一个状态集合{s1,s2,s3},首先,一个时间序列t1,t2,t3,...中t时刻选取的状态是随机的,如序列
。第二,任一状态
的取值可能与周围其它的状态有关。这样随机状态就有了两个维度的不确定性。马尔可夫为了简化问题,提出了一种简化的假设,即随机过程中各个状态
的概率分布,只与它的前一个状态
有关,即
。当然这种假设未必适合所有的应用,但是至少对以前很多不好解决的问题给出了近似解。这个假设后来就命名为马尔可夫假设,而符合这个假设的随机过程则称为马尔可夫过程,也称为马尔可夫链。下图给出一个离散的马尔可夫过程。
在这个马尔可夫链中,四个圈表示四个状态,每条边表示一个可能的状态转换,边上的权值是转移概率。如果某个时刻t的值为m2,那么t+1时刻有40%的可能为m4,60%的可能为m3,因为t+1时刻的值只与t时刻有关系,和t-1时刻没关系。
把这个马尔可夫链想象为一台机器,它随机的选择一个状态作为初始状态,然后按照上述规则随机输出状态,运行一段时间T后,我们会得到状态序列:。看到这个序列,不难数出某个状态
出现的次数#(
),以及
转换到
的次数#(
)。
到
的转移概率可以通过#(
)/#(
)得到。
隐含马尔可夫模型是对上述马尔可夫链的一个扩展:任意时刻t的状态是不可见的,所以我们不能通过观察序列直接获得转移概率。但是隐含马尔可夫模型在每个时刻t都有一个输出
,且
仅与
相关。这个被称为独立输出假设。简而言之,序列
是由一个马尔可夫链产生的,并且
到
符合独立输出假设,就是隐含马尔可夫模型的结构了。如图:
由于序列是基于马尔可夫假设的,所以5.3式的右半部分等价于
由于独立输出假设,所以5.3式的左半部分等价于
这样通信的解码问题就可以用隐含马尔可夫模型来解决了。至于如何找出式子的最大值,可以使用维特比算法(Viterbi Algorithm)。
延伸阅读:隐含马尔可夫的训练
围绕着隐含马尔可夫模型有三个基本问题:
- 给定一个模型,如何计算某个特定的输出序列的概率
- 给定一个模型和某个特定的输出序列,如何找到最可能产生这个输出的状态序列
- 给定足够量的观测数据,如何估计隐含马尔可夫模型的参数
第一个问题很简单,对应的算法是Forward-Backward算法。第二个问题使用著名的维特比算法解决。第三个问题在此讨论。
转移概率(Transition Probability)和生成概率(Generation Probability)
被称为隐含马尔可夫模型的参数,而计算和估计这些参数的过程称为模型的训练。
从条件概率的定义出发,如果我们有足够多的人工标记的数据,生成概率可以通过观测次数得到:
跟前面求马尔可夫链的转移概率一样,如果我们有大量人工标注的数据,通过统计次数就可以估计转移概率:
然而有些情况下我们无法做出标注,有些情况下标注的成本较大,比较实用的方式是直接通过观测序列就能推测出模型的参数,这类方法叫做无监督的训练方法,其中主要使用的鲍姆-韦尔奇算法(Baum-Welch Algorithm)。
两个不同的模型可以产生同样的输出序列,但总会比另一个
更有可能产生观测序列,其中
为模型的参数。鲍姆-韦尔奇算法就是用来寻找这个最可能的模型
.
鲍姆-韦尔奇算法思想:
首先找到一组能够产生输出序列O的模型参数(显然他们是一定存在的,假设转移概率P和输出概率Q为均匀分布时,模型可以产生任何输出)。现在,有了初始模型,需要在此基础上找到更好的模型。假定我们解决了第一个和第二个问题,那么我们可以求出当前模型产生输出O的概率,及产生输出O的可能状态序列及这些状态序列的概率。把这些可能的状态序列看做是“标注的训练数据”,我们可以计算出一组新的模型参数
,并且可以证明模型1的O输出概率大于模型0的输出概率,如此循环往复,直到模型的质量不再显著提高为止。
鲍姆-韦尔奇算法的每一此迭代都是不断的估计(Expectation)新的模型参数,使得输出的概率(我们的目标函数)达到最大化(Maximization),因此这个过程被称为期望最大化(Expectation-Maximization),简称EM过程。EM过程保证算法一定能收敛到一个局部最优点,很遗憾它一般不能保证找到全局最优点。因此,在一些自然语言处理的应用,比如词性标注中,这种无监督的鲍姆-韦尔奇算法训练出的模型会比有监督的训练得到的模型效果略差,因为前者未必能收敛到全局最优点。但是如果目标函数是凸函数(比如信息熵),则只有一个最优点,这种情况下EM过程可以找到最佳值。
小结
隐含马尔可夫模型最初应用于通信领域,继而推广到语音和语言处理中,成为连接自然语言处理与通信的桥梁。同时,隐含马尔可夫模型也是机器学习的主要工具之一。和几乎所有的机器学习的模型工具一样,它需要一个训练算法(鲍姆-韦尔奇算法)和使用时的解码算法(维特比算法)。掌握了这两类算法,就基本上可以使用隐含马尔可夫模型这个工具了。