线性模型，线性回归，对数几率回归(Logistic regression)的理解与推导(深度学习前戏( ╯□╰ ))

对数几率回归（logistic regression），有时候会译为逻辑回归(音译)，其实是我们把回归模型应用到分类问题时，线性回归的一种变形，主要是针对二分类提出的。既然是线性回归的一种变形，那么在理解对数几率回归时，我们先来了解一下什么是线性回归。

1.线性回归

1. 1线性方程

形如
$f(x)=w_1x_1 + w_2x_2 + w_3x_3 + ... + w_dx_d + b$
我们称为线性方程，即任何变量都是一次幂的函数，向量形式一般写成：
$f(x) = \mathbf w^T\mathbf x+b$
不难看到如果我们将其中的 $w = (w_1;w_2;w_3;...;w_d)$与 $b$学习得到之后，我们就得到了一个固定的线性模型，这个模型对应了某些量之间的一种映射，可以拿来作为预测。线性模型形式简单但是却蕴含着机器学习中一些重要的基本思想。许多功能更为强大的非线性模型都是从线性模型的基础上通过引入层级结构或者高维映射得到的。此外，如果我们仔细分析的话，可以发现 $w$ 其实是每个变量对这个模型重要程度(即权重)的集合，使得线性模型有很好的可解释性。

1. 2线性回归

线性回归本质就是预测一个连续的输出，即根据我们手头上拥有的数据集 $D= \{(\mathbf x_1,y_1),(\mathbf x_2,y_2),...,(\mathbf x_m,y_m)\}$其中 $x_i = (\mathbf x_i^1;\mathbf x_i^2;\mathbf x_i^3;...;\mathbf x_i^d),y_i \in\mathbb R$
学习到一组w与b，使得这个模型能够尽可能准确地预测实值输出标记。
那么如何准确的去学习出这组 $w$与 $b$呢？
我们先考虑一种最简单的情况那就是只有一个输入 $w_i$,所以学习的结果其实就是使 $f(x_i)\approx y_i$,我们知道均方误差使回归任务中最常用的性能度量，因此我们只要找到使得两者均方误差最小的那组 $w$与 $b$，我们就得到了相对预测最准确的模型。
均方误差最小，即：

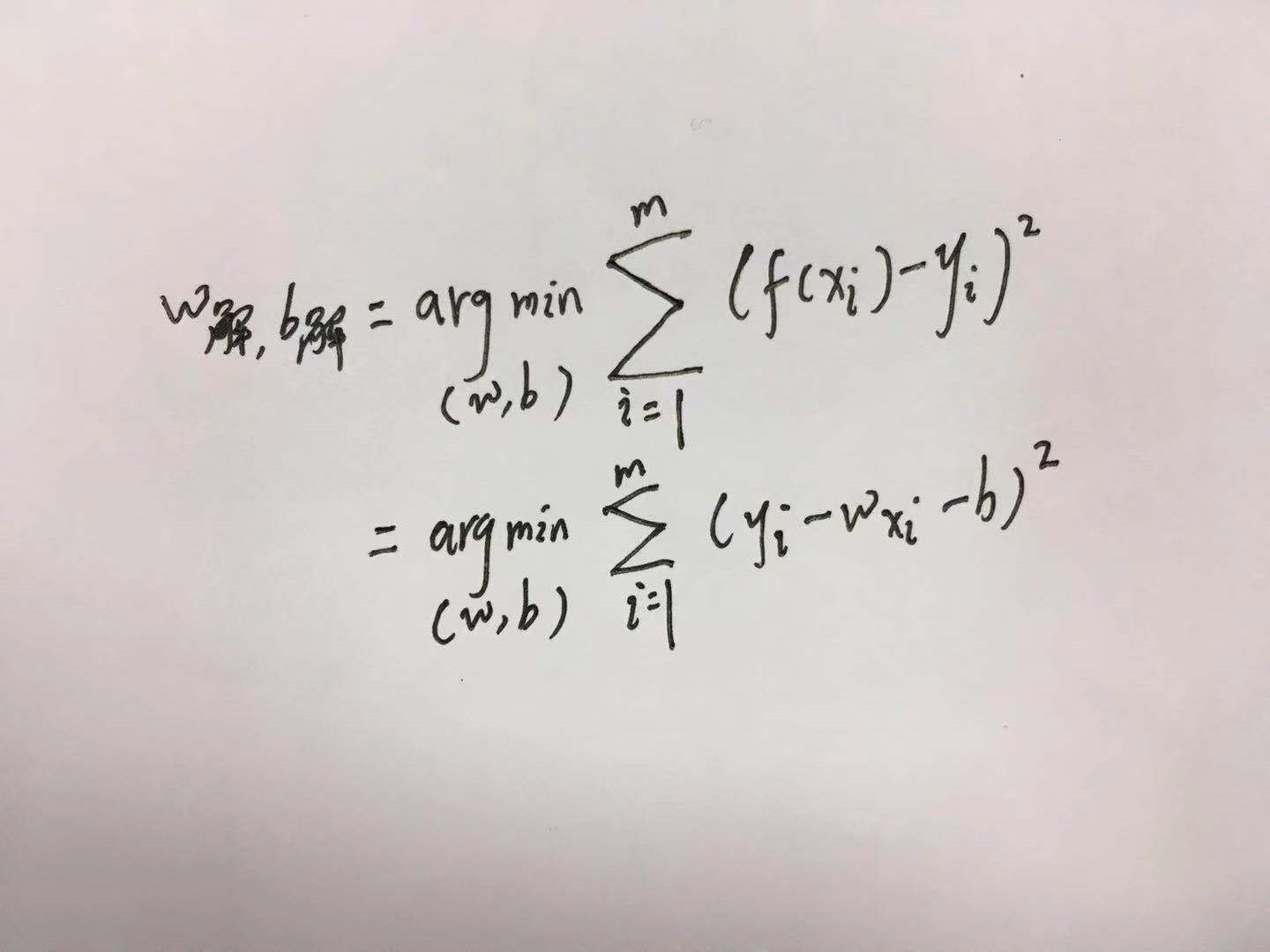
这种基于均方误差最小化来进行线性模型求解的方法称为”最小二乘法”(least square method),线性回归中最小二乘法就是找到一条直线，使得所有样本到直线上的欧氏距离最小。
这个求解过程也被称为线性回归的最小二乘参数估计。
$E_{(w,b)} = \sum_{i=1}^m(y_i - wx_i - b)^2$

$\frac{\partial L(w,b)}{\partial w} = -2 \sum_{i=1}^m(x_iy_i - wx_i^2 - bx_i)$
我们知道形如 $y=x^2$函数通常是凸函数，且极值点在导数为0时取得。
于是我们分别对 $w$与 $b$求导得到:

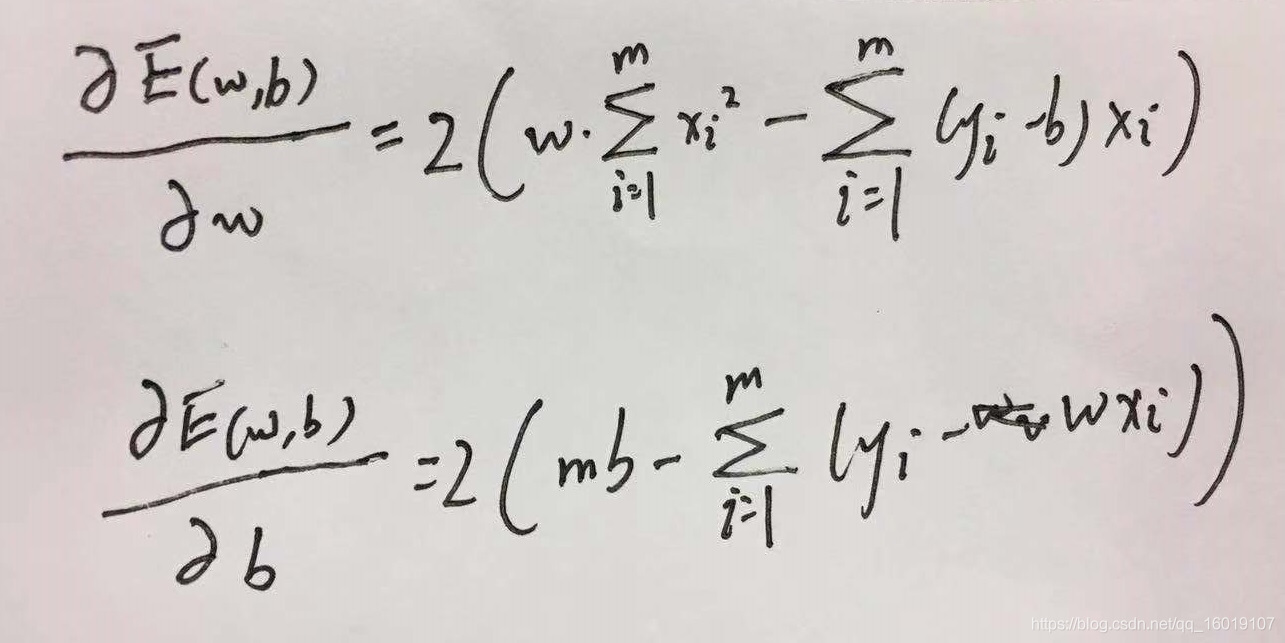
令二式均为0就可以得到w与b最优解的闭式解：

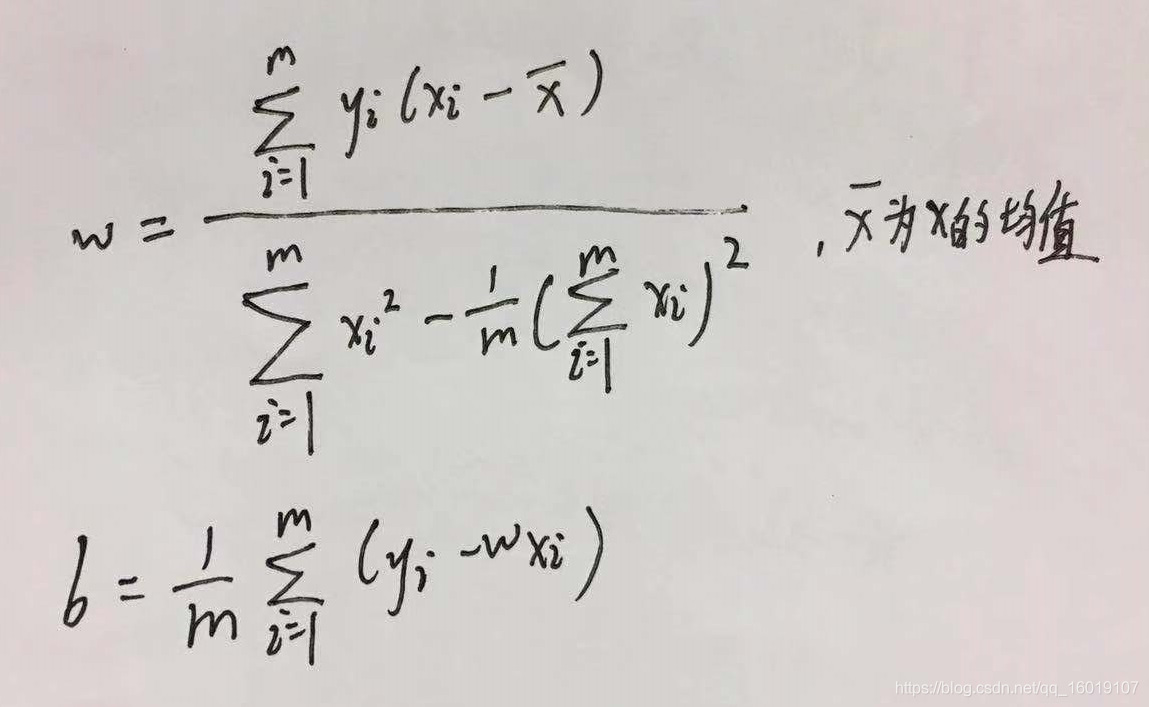
这里可以提一下什么是闭式解，闭式解其实就是解析解，与数值解相对应，最笼统的解释解析解就是严格按照公式推导出来的解，而数值解是按照特定条件近似计算得到的基本满足的数值，逼近解析解，但是正确性没有解析解来的好。
那么当我们的输入是多个变量的时候该怎么办呢。
其实就是把 $w$与 $x$向量化，即我们试图学得 $f(\mathbf x_i)=\mathbf w^T\mathbf x_i+b$,使得 $f(\mathbf x_i)\approx y_i$，这就是多元线性回归
我们同样利用最小二乘法对 $w$与 $b$进行估计。我们将 $w$与 $b$结合得到 $\hat \mathbf w =(\mathbf w;b)$,同时把数据集D表示为一个 $mX(d+1)$大小的矩阵X 最后一个元素恒为1。

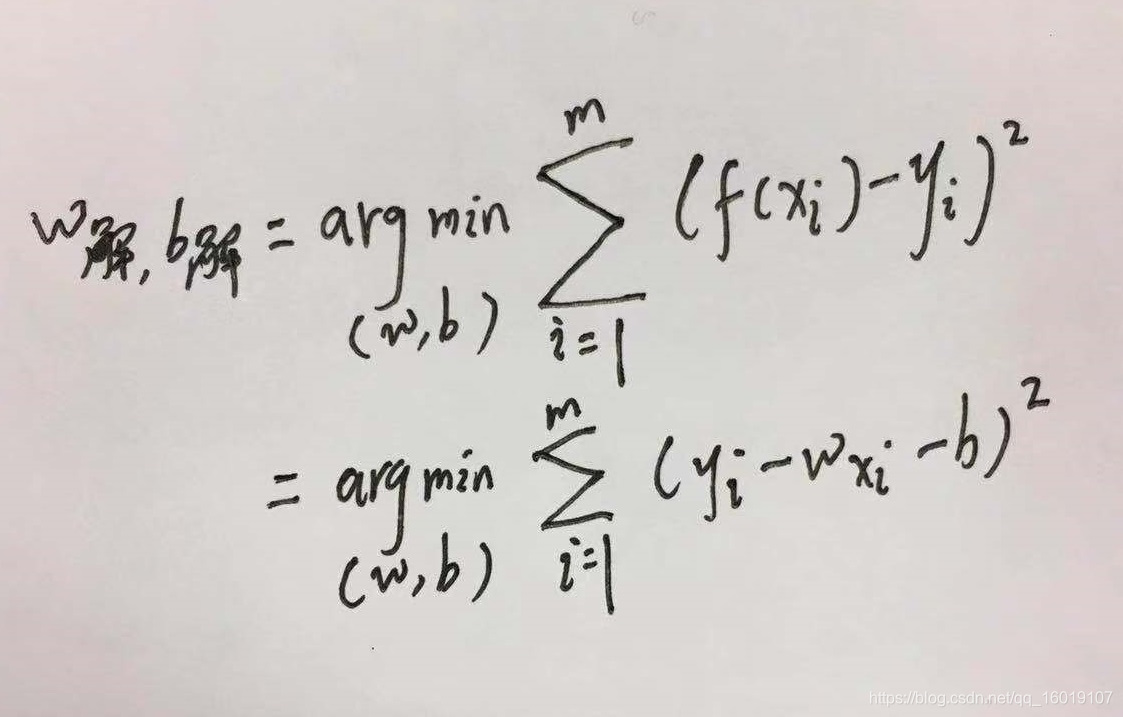
于是上图可以化为：

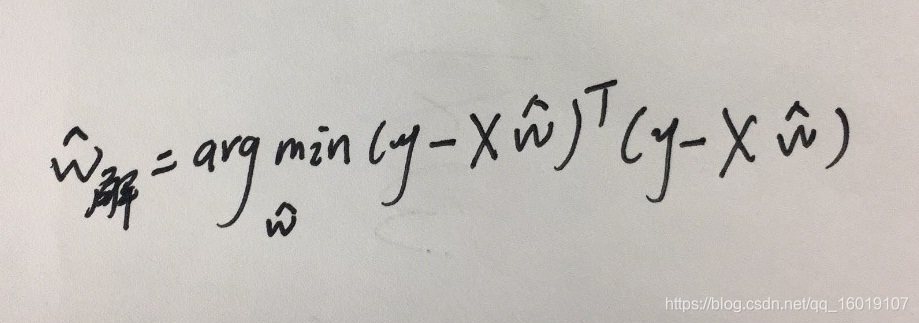
令 $E_{\hat w}=(\mathbf y-\mathbf X\hat \mathbf w)^T(\mathbf y-\mathbf X\hat \mathbf w)$,对 $\hat \mathbf w$求导，推导过程如下：

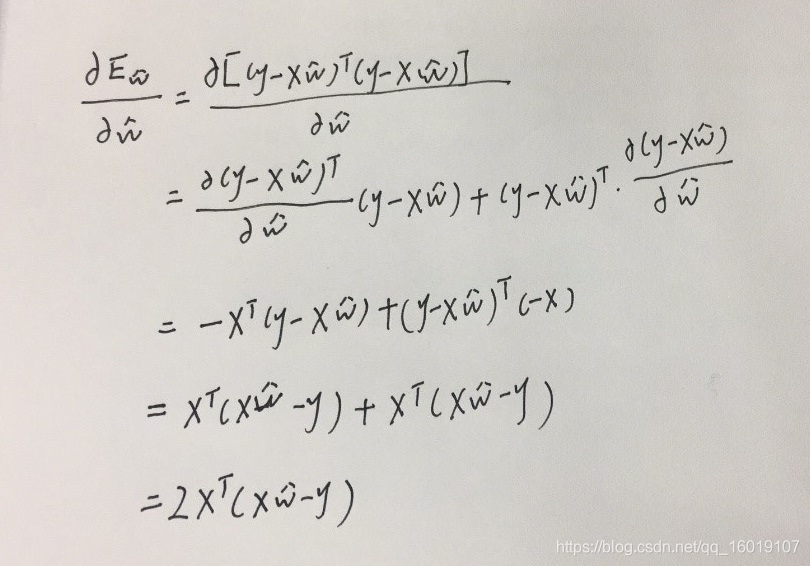
只有当 $\mathbf X^Τ \mathbf X$为满秩矩阵或者正定矩阵时，令上式为0可以求得唯一解，但是现实中，我们碰到的往往都不满足满秩矩阵或者正定矩阵的情况，因此我们可以求得多个 $\hat \mathbf w$使得均方误差最小，常见的方法是引入正则项化（下次再议）
当然线性模型会有很多种变形如：
$\ln y=\mathbf w^T\mathbf x_i+b$

其实就是就是一种让输出标记在指数尺度上变化的形式，被称为对数线性回归。

2.对数几率回归

虽然名字叫做回归。但是千万别把他看成一个回归问题，对数几率回归本质上处理的分类问题。考虑最基本的二分类问题。那么我们的理想输出应该是1或0，即是或者不是。但是知道线性模型

$f=\mathbf w^T\mathbf x+b$
产生的预测值是一个实数，我们只要想一个办法将预测值转化成为1或者0两个值，是不是就可以将回归问题转化为分类问题了呢？
怎么转化呢，最简单的方式肯定是分段函数直接截取最后预测值进行分段，如下所示
$y = \begin{cases} 1, & \text{if $f$ > 0} \\ 0.5, & \text{if $f$ = 0} \\ 0, & \text{if $f$ < 0} \\ \end{cases}$
若 $f$大于0则 $y=1$，即为正例，若 $f$小于0则 $y=0$，即为反例，若 $f=0$则 $y=0.5$，即可以任意判别此例。
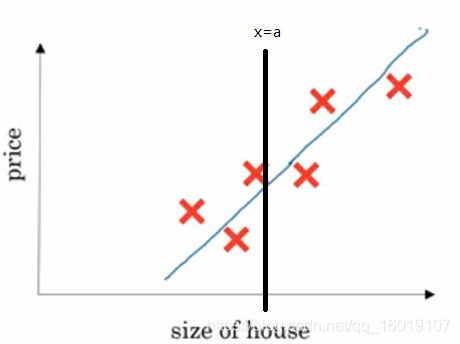
这里你们肯定不经想问为什么是以预测值 $f$大于小于等于0作为分界线的？让我们回到最初的线性方程，如下图所示,根据房间大小预测房价。我们可以看到当 $f=0$的时候，其实是预测点刚好落在这条线上，在分类问题中这条线我们称之为分界线。我们任意取一个输入 $x=a$，画一条竖线，我们可以看到分界线把 $x=a$分成了三部分，上方，下方，和相交的那一点。在上方的点对于这条预测线来说，价格都是偏高的，因此可以归类为价格高这个属性即 $y=1$而下方都是偏低的，归类为 $y=0$，而在这条预测线上的点，我们无法定义他的价格属于高还是低，因此可以作为任意判别。

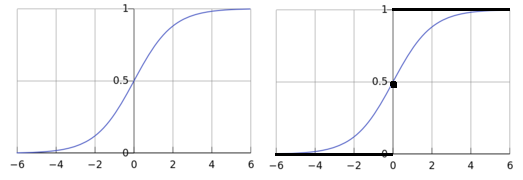
再回到那个分段函数，我们把这种非常理想的函数形式称为“单位阶跃函数”(Heaviside函数)如上图黑线黑点所示。但是我们不难发现这种函数是不连续的，不可微，不可微带来的问题就是我们不能求解最佳的 $w$与 $b$。那么我们就想呀，我们要找到一种形似单位阶跃函数却又单调可微的函数，那多简单，让它弯曲起来呀，于是我们就找到了上右图蓝色的函数形式，这个就是对数几率函数，它的解析式为：
$y = {1 \over 1 + e^{-f}}$
从函数形式上不难看出，它将f值转化为一个接近1或者0的y值，并且让f=0附近的时候变化很剧烈。这部分不就是分界线附近的时候嘛，根据这个特点，不难看出来这个函数可以让我们更好的完成分类问题。
我们将之前 $f$的完整式带入得到:

$y = {1 \over 1 + e^{-f}} = {1 \over 1 + e^{-(w^Tx+b)}}$
做一个对数形式的变换可以得到:
$ln{y \over 1 - y} = w^Tx + b$

回到我们最初的定义，我们将 $y$定义为测试样本 $x$是正例的可能性（越大就越可能是正例，1的时候一定是），反之 $1-y$就是测试样本 $x$为反例的可能性。那么两者的比值就更加显化了测试样本 $x$为正例的相对可能性，因为当比值大于1的时候就是测试样本 $x$为正例的可能性要大于为反例的可能性，我们将这个比值称为几率:
$y \over 1 - y$

对几率取对数就得到了对数几率，由于对数与几率在对应区间内单调性相同，因此对数几率仍然反应了测试样本x为正例的相对可能性。
$ln{y \over 1 - y}$
因此我们只要确定最优的 $w$与 $b$就可以找到那个最优的分类模型了。求最优解，就是求一个极值，我们在线性回归当中提到，一般的线性模型并不一定只有一个最优解，而严格的凸函数才有唯一的最优解
那么对数几率回归的目标函数
$ln{y \over 1 - y} = w^Tx + b$
是不是一个严格的凸函数呢？
证明一个函数是严格凸函数，我们可以从二阶导恒大于0入手

那么我们该怎么求解 $w$与 $b$呢？这个时候我们可以从极大似然法入手。首先我们将 $y$视为类后验概率估计 $p=(y=1|x)$,于是得到：

$\begin{cases} y &= p(y=1 | x) = {e^{w^Tx + b} \over 1 + e^{w^T+b}} \\ 1 - y &= p(y = 0 | x) = {1 \over 1 + e^{w^T+b}} \end{cases}$
这时候我们可以用极大似然法来估计 $w$与 $b$。对于给定的数据集 ${(x_i,y_i)}_{i=1}^m$
那么对数几率回归模型最大化的对数似然为：

$\ell_{(w, b)} = \sum_{i = 1}^mlnp(y_i | x_i; w,b)$
为了便于讨论，令 $Q=(w,b),\hat w =(w;1)$,则 $\hat w^Tx+b$可简写为 $Q^T \hat x$,再令 $p_1 {(\hat w ;Q)}=p(y=1│\hat w ;Q),p_0 (\hat w ;Q)=p(y=0│\hat w;Q)=1-p_1 (\hat w;Q)$上式的概率部分可以重写为：
$p(y_i | x_i; w,b)=p_1(\hat {x_i};Q)^{y_i}p_0(\hat {x_i}; Q)^{1 - y_i}$

带入到对数似然式子中得到：
$\ell_{(w, b)} = \sum_{i = 1}^m(-y_iQ^T\hat x_i+\ ln(1+\boldsymbol e^{Q^T\hat x_i}))$
最大化最上面对数似然等价于最小化上式。但是这个时候有个前提，那就是上式是个严格凸函数才有唯一最小值。能不能证明呢？当然能啦，证明过程如下：

根据凸优化理论，可以利用梯度下降法或者牛顿法等数值优化算法来求Q的最优解。