LCA的各种解法见:July的《程序员编程艺术:面试和算法心得》电子版(非官方)。
下面只讲Tarjan算法解决这个问题的方法,本质上仅仅是普通的dfs而跟Tarjan算法是没关系的,只是因为思路像所以这么说。它解决LCA是离线处理的,即等待全部输入完后一起处理再输出,而Tarjan好处在于查询次数再多也只需要遍历一次树。
思路
对树进行一次深搜遍历,遍历中做此操作:
假设当前遍历到 t 这个顶点,每遍历 t 的一个子树就把子树和 t 点归为一个集合,且设定这个集合的祖先是 t 。
遍历完所有子树后遍历跟 t 点相关的查询,若另外个点已经访问过,则这次查询的LCA就是另外个点所在集合的祖先。
伪代码
void dfs(int u){
设定u为已访问
设定u的祖先为u自身
遍历u的所有邻接点v
若未访问过,则dfs(v),合并u所在集合和v所在集合为一个新集合,设定新集合的祖先为u
若访问过则不再访问
检查跟这个u点有关的查询(u,v)
若v已访问,则lca = v所在集合的祖先
若v未访问不做处理
}
原理
对查询边(u,v),只有下面两种情况:
1) u,v在t的同一个子树下,则u,v中距离整个树的根最近的就是LCA。
假设u点在上v在下,在搜索到u点时去递归遍历u的子树(里面含v),遍历完这棵子树之后按照操作规则,子树就和u合为一个集合且集合祖先为u,然后在u点遍历完所有子树后就检查(u,v)查询发现v已访问过,一查v所在集合的祖先不就是u么。
2) u,v在t的不同子树下(如在二叉树中则是一左一右),则t点就是lca,一看图就知道。
假设u已经被遍历过了(u肯定在某个t的集合里且集合祖先为t),则访问到v(不同子树意味着v肯定在u这个集合之外)时,直接找u点所在集合的祖先就是u,v点的LCA。
例子
为方便描述,盗上面链接的图
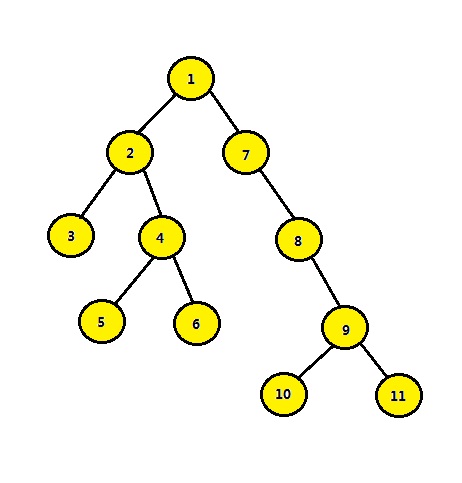
比如查询(5,6)和(3,5),而搜索从1号开始,当前遍历到2号点,然后递归遍历5,6点,先遍5号点,5号点没有子树了,就直接查询跟5号点相关查询,发现对应的6号点没访问过,先跳过不管(没访问过的没有信息去判断)。
根据递归性质返回2号点,把2和5合成一个集合{2,5},集合祖先为2。接下来去访问6,6也没有子树,然后有(5,6)这个查询,就直接查询5所在的集合祖先,嗯就是2。
之后返回2号点,把{2,5}和{6}合并成{2,5,6},祖先设为2。
返回1号点,把{2,5,6}和{1}合并成{1,2,5,6},祖先为1。
去访问1的其他子树比如3,到3号点去遍历3的全部子树,这里略过子树访问说明,访问完3的全部子树返回3后{3,7,8,9,10,11,12}的祖先是3,然后找到跟3有关的查询(3,5),直接查询5所在集合的祖先,嗯就是1啦!
例子中得到的结论
- 例子的遍历顺序不一定是子树就按图中画的从左到右,也可以先访问到3这个子树再去2号子树,这跟加边顺序有关,不过结果一样,不过发现答案的时候是这次查询的另外一个点而已。【这意味着代码中查询的边要设为双向】
- 对于每个点所在的集合、所在集合的祖先是在遍历过程中一直改变的,集合的大小一直在增大,而祖先就越来越靠近整棵树的树根。
- 集合怎么表示?并查集啊。
结合下面代码去看上文的图很好理解的
验证的话可以提交到 POJ 1330 Nearest Common Ancestors
虽然题目是只查询一次,可以水,不过我们就当作是多次查询来算
#include <cstdio>
#include <cmath>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
#define clr( a , x ) memset ( a , x , sizeof (a) );
#define RE freopen("1.in","r",stdin);
#define WE freopen("1.out","w",stdout);
#define SpeedUp std::cout.sync_with_stdio(false);
#define debug(x) cout << "Line " << __LINE__ << ": " << #x << " = " << x << endl;
const int maxn = 10005;
const int maxm = 10005;
const int inf = 0x3f3f3f3f;
const int maxq = 1;
int eCnt;
int head[maxn];
struct Edge
{
int v, next;
} edge[maxm];
void addEdge(int u, int v) {
edge[eCnt].v = v, edge[eCnt].next = head[u]; head[u] = eCnt++;
}
//---离线处理用到的查询
int ans[maxq];
int qCnt;
int qHead[maxn];
struct Query
{
int v,next;
int index; //查询的编号
}query[maxq*2];
void addQuery(int u, int v,int index) { //双向,因为查u,v和查v,u是一样的
query[qCnt].index = index;
query[qCnt].v = v, query[qCnt].next = qHead[u]; qHead[u] = qCnt++;
query[qCnt].index = index;
query[qCnt].v = u, query[qCnt].next = qHead[v]; qHead[v] = qCnt++;
}
//---并查集
int father[maxn];
int find(int x){
if(x != father[x]){
father[x] = find(father[x]);
}
return father[x];
}
void merge(int x,int y){
x = find(x);
y = find(y);
if(x != y)
father[y] = x;
}
int du[maxn];
int vis[maxn];
void init(){
clr(head,-1);
clr(qHead,-1);
clr(vis,0);
eCnt = 0;
qCnt = 0;
clr(du,0);
}
void lca(int u){
vis[u] = 1;
//遍历u点的邻接边
for (int i = head[u]; ~i; i = edge[i].next){
int v = edge[i].v;
if(vis[v]){
continue;
}
lca(v);
merge(u,v); //注意此处应该把 u 设置为 v 的父节点,不能反,因为u在树上就是v的父/祖先节点
}
//找跟当前u点有关的查询,这个uv查询的答案是v点所在集合的祖先
for (int i = qHead[u]; ~i; i = query[i].next){
int v = query[i].v;
if(vis[v]){
ans[query[i].index] = find(v);
// debug(u)debug(v)debug(find(v))
}
}
}
int main() {
// RE
int t;
int n,u,v;
while(scanf("%d",&t)!=EOF){
while(t--){
init();
scanf("%d",&n);
for (int i = 1; i <= n-1; ++i){
scanf("%d%d",&u,&v);
addEdge(u,v);
du[v]++;
father[i] = i; //每个结点的父亲/祖先 都初始化为自己
}
father[n] = n;
int queryCnt = 1; //查询次数
for (int i = 1; i <= queryCnt; ++i){
scanf("%d%d",&u,&v);
addQuery(u,v,i);
}
//找入度为0的点当树根
int root = 1;
for (int i = 1; i <= n; ++i){
if(!du[i]){
root = i;
break;
}
}
lca(root);
for (int i = 1; i <= queryCnt; ++i){
printf("%d\n", ans[i]);
}
}
}
return 0;
}