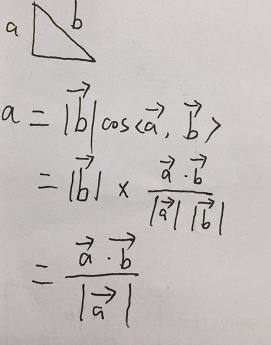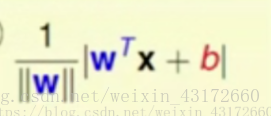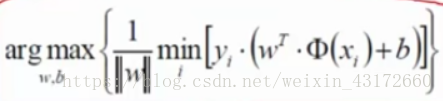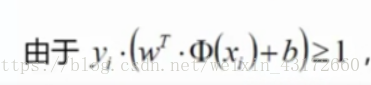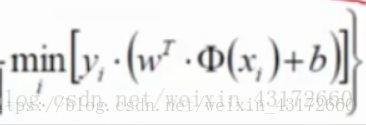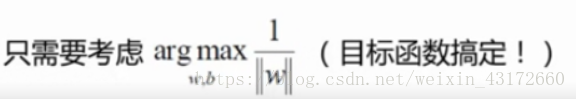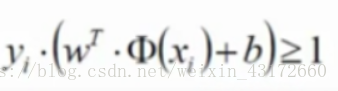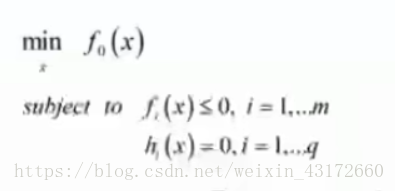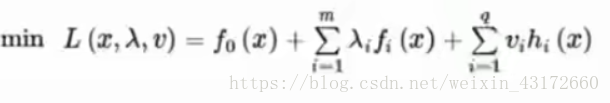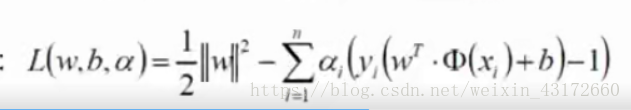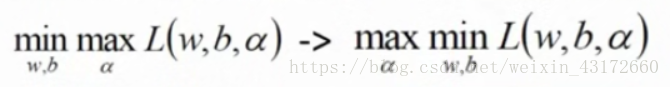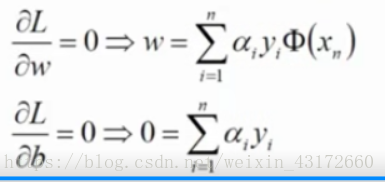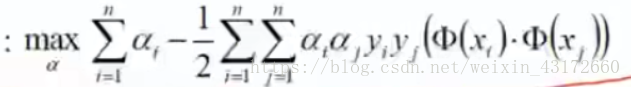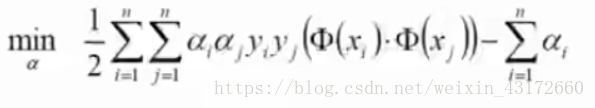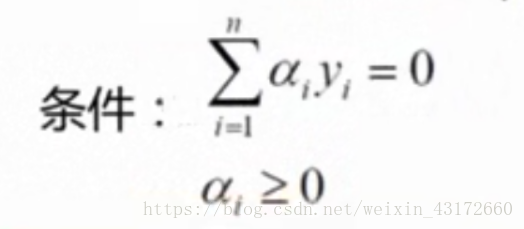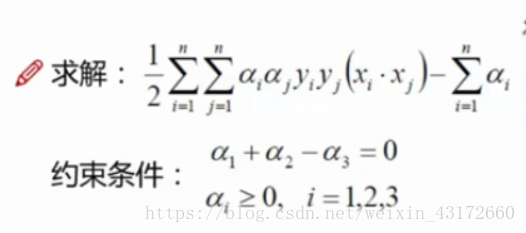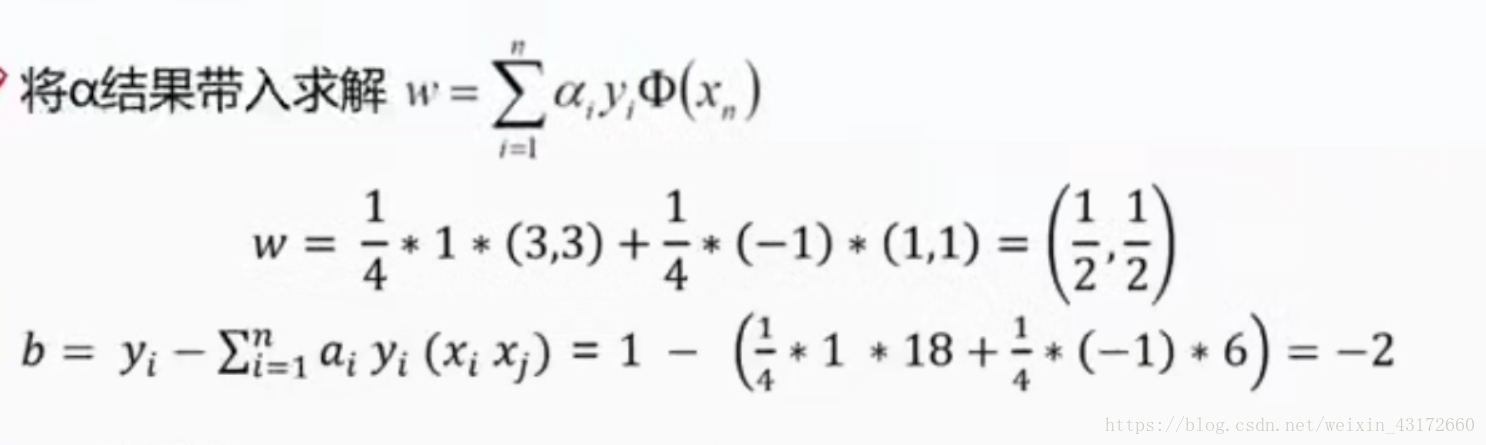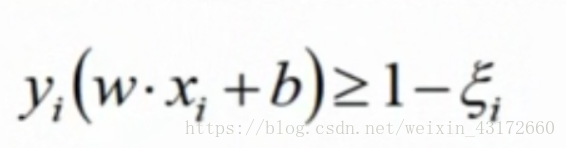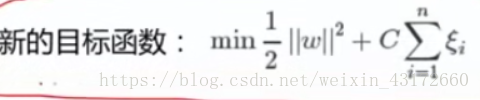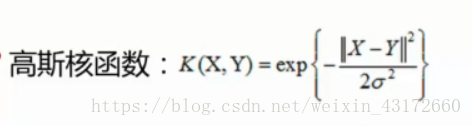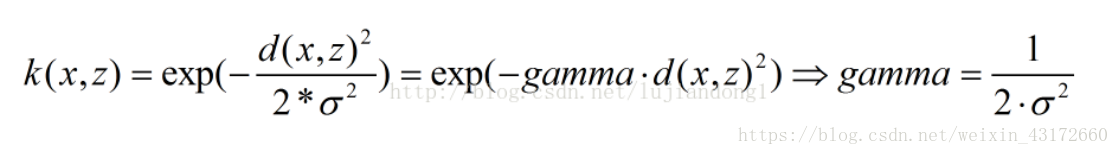机器学习支持向量机（SVM）的理解和推导

支持向量机（support vector machines）

支持向量机是机器学习中的一种很重要的算法，相比于其他算法，支持向量机的优势在于能够通过核技术将数据从低纬度映射到高纬度来划分数据集。原则是使决策边界最大化。下面一步步推导过程。

决策边界

首先给大家一个概念，什么是决策边界。
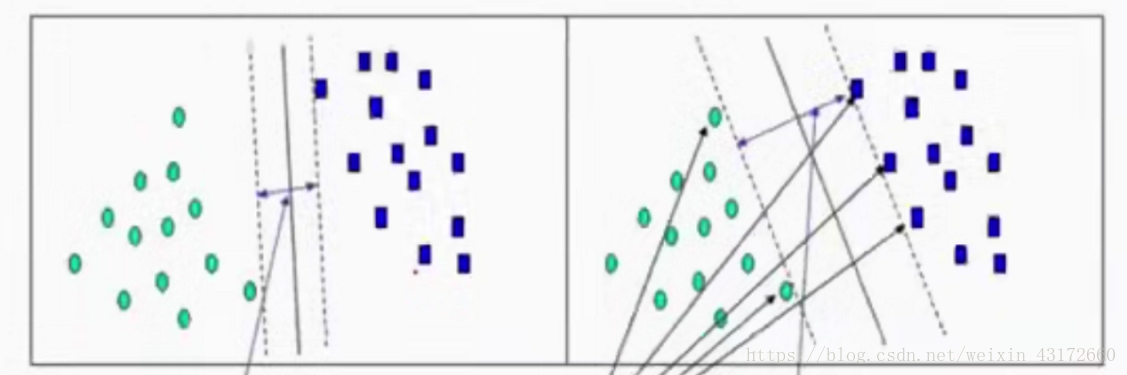
下图两堆数据集可以看成是国家战争边界，绿色点和蓝色点是两个国家埋的地雷，假设有一个军队要穿过这个地雷带，怎样穿过去才更安全呢，若按照图一那样穿过去，会比图二那样穿过去更加危险，我们把这个边界叫做决策边界。我们要解决的就是寻找这个决策边界的最大值。这样穿过去才会更加安全（分类效果更加的好）
在这里插入图片描述

距离的计算

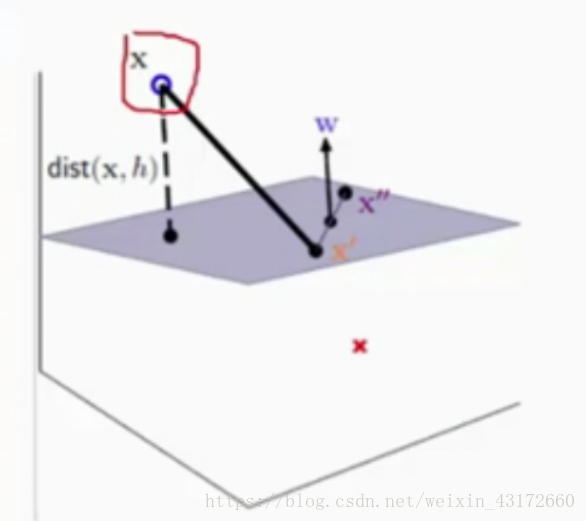
不管这个数据是几维的，我们假设这个决策边界为 $w^T$ x+b=0（数据是二维的话，边界是一条直线，数据是三维的话，边界是一个平面），下面是一个三维的边界。
在这里插入图片描述
要求点x到边界的距离，可以用xx‘ 在垂直方向的映射来求。
假设x’是平面上的点存在 $w^T$ x‘+b =0 即 $w^T$ x’=-b
因为在 $w^T$ x+b中， $w^T$ 是x垂直于平面的向量，也就是法向量，|W|是法向量长度
要求 b在a方向上的投影可以用下面的公式
在这里插入图片描述
解释一下下面公式的意思
根据上面公式可求解第一步
$w^T$ (x-x’) 展开为 $w^T$ x- $w^T$ x’ 因为 $w^T$ x’=-b 所以 $w^T$ (x-x’) =| $w^T$ x+b|（因为距离，所以要加上绝对值）

上面的距离便是我们进一步的目标函数，要使这个距离最大化

数据标签定义

因为要分类，所以所有数据集都有标签，我们设当X为正例的时候 Y= +1, 当X为负例的时候Y= -1
决策方程为下图方程暂且把决策方程看成y= $w^T$ x+b 图中是对x做了变化的（涉及到核变化），最后面会做说明。
当y(xi) >0 ==> yi =+1
当y(xi) <0 ==> yi =-1
综合起来 yi*y(xi) 恒大于0 这个性质等下会用到
在这里插入图片描述

优化目标

我们要清楚我们要求的是什么，支持向量机就是围绕这个东西来玩。

通俗解释：找到一条直线（w和b）使得离该线最近的点最远。

从上面求出的点到面的距离：
在这里插入图片描述
因为| $w^T$ x+b|恒大于0 ，在前面数据标签定义最后得到的式子也是恒大于0 所以可以化简为没有绝对值的形式。可以化简为：

对于决策方程，我们可以通过放缩使得其结果值≥1
在这里插入图片描述

根据我们的通俗解释 :找到一条直线（w和b）使得离该线最近的点最远。

可以把上面的式子转化为：
在这里插入图片描述
min括号内是指寻找离这条线最近的点，外面max是找地雷，使地雷到决策边界的距离越大越好。

然后因为下面的式子恒大于1
在这里插入图片描述
所以min为1，我们只需要求1/|w|的最大值

所以现在的目标函数为：

我们可以把求极大值的问题转化为求极小值的问题：1/2 $w^2$ 的最小值（1/2为了后面方便求导运算）

不要忘了！我们这个式子是在下面条件的约束下才成立的。
在这里插入图片描述

拉格朗日乘子法

要求方程在约束条件下的极值问题，可以用拉格朗日乘子法。

如下图，当要求f0(x)的极小值，但约束于一些条件时，这里的约束条件可以是不等式约束和等式约束，下面f1(x)是不等式约束，而h1(x)是等式约束。
在这里插入图片描述
都可以将式子转化为下图形式：

而我们的目标函数只有一个约束条件，所以可以把原始转化为：

我们可以根据拉格朗日里面的KKT性质，为了方便计算和后面进行核变化更容易
（这里看到一篇介绍这个性质的，可以参考一下
https://blog.csdn.net/bit_666/article/details/79865225）
将式子转化为下面这个式子，先求这个式子的最小值再求最大值。

在这里插入图片描述
我们先求最小值，对于当前式子来说，什么样的w和什么样的b能让式子最小，说到最小值，我们要求偏导，分别对w和b求偏导，得到：

将偏导后的结果代入，得到下面的式子，整个推导过程如下：

接下来对a求极大值，
在这里插入图片描述
可以将问题转化为求极小值问题，

别忘了，还有条件，第一个是我们偏导后求出来的，第二个是拉格朗日乘子法需要满足的条件。

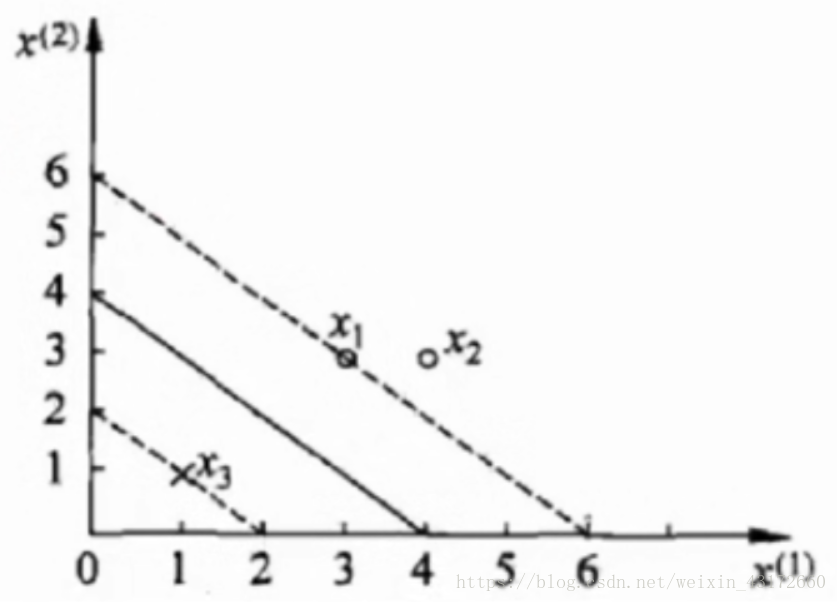
α怎么求呢，α的求解是比较麻烦的，我们通过一个比较简单的例子来求解

在这里插入图片描述
中间的实线是决策边界 x1(3，3)和x2(4，3)是正例，每个点都有一个α，y=+1，x3(1,1)是负例，y=-1

在约束条件那里，我们可以得到α1+α2=α3 ，将数据代入上面式子，得到

那要求极小值，怎么求，还是求偏导，对α1和α2求偏导，得到α1=1.5，α2=-1，但是并不满足第二个约束条件，所以解应该在边界上，那么应该是α1=0 或者是α2=0，代入得
在这里插入图片描述
接着把结果代入到之前求偏导得到的w式子里，b也可以根据y-wx求得

这样就可以求得平面方程为0.5x1+0.5x2-2=0

现在我们要来讲这个算法为什么叫做支持向量机了。
机指的是决策边界
这个边界是由x1，x3这些对应的α非0的向量支持的，是是支持向量，真正发挥作用的数据点。

软间隔

有时候数据会有一些噪音点，我们可以加入松弛因子，也就是说放松一点，边界不要那么严格。

我们可以在决策方程体现这一点，
在这里插入图片描述
既然引入了新的条件，我们需要有新的目标函数

当C越大，参数越小，分类越严格
当C越小，参数可以很大，分类可以有错误容忍
C是我们调包的时候需要调的一个参数

同样运用拉格朗日乘子法，可以得到下面的公式。相比于之前的式子，只是约束条件变了。

在这里插入图片描述

核变化

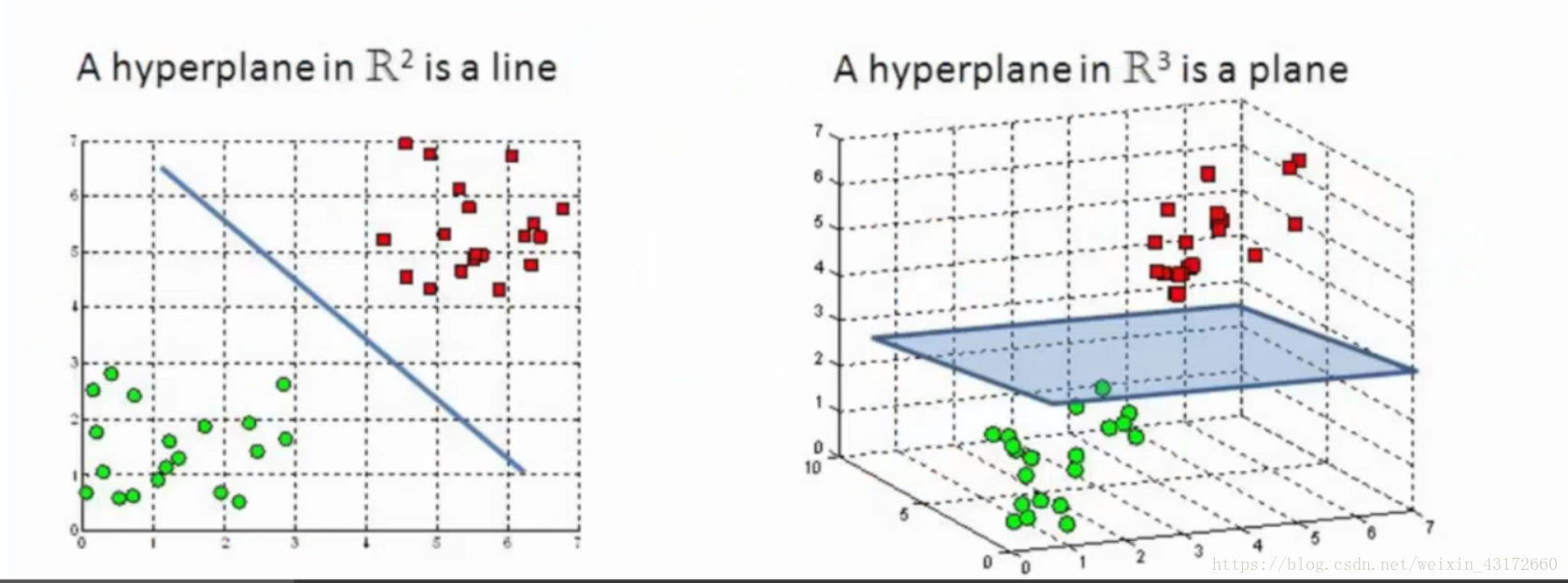
下面来讲支持向量机最最核心的部分，核变化。通过核变化，可以将数据从低纬度映射到一个高纬度的空间，便于分类。下面右边的图是三维的，相比于左边二维的图，是不是更容易分类了呢。
在这里插入图片描述
面试的时候会有人经常问，你核变化了之后，数据真的到一个高维的空间计算了吗。
下面举一个小例子，假设有两个数据，x=（x1，x2，x3） y=（y1，y2，y3）这两个数据是三维的，但在三维空间已经没有办法对他进行分类的，我们可以通过一个函数将其变成更高维的空间，比如九维的话，f（x）=（x1x1，x1x2，x1x3，x2x1，x2x2，x2x3，x3x1，x3x2，x3x3），由于在前面的式子里，数据之间需要求内积，所以在新的空间里，需要花费O（ $n^2$ ）。
具体点，x =（1，2，3） y=（4，5，6），f（x）=（1，2，3，2，4，6，3，6，9），
f（y）=（16，20，24，20，25，30，24，30，36）
<f(x),f(y)>=16 + 40 + 72 + 40 + 100 +180 + 72 + 180 +324 =1024
现在在九维的情况下，似乎还能计算，但当数据映射到更好维度的时候，计算量就很大很大了。
但是我们发现K<x,y>=(<x,y>)² =（4+10+18）²=1024
这和<f(x),f(y)>得到的结果是一样的。但效率却提高了，花费O（n）。
所以核函数的好处就是，可以在一个低维空间去完成高维空间样本内积的计算，效率还很高。