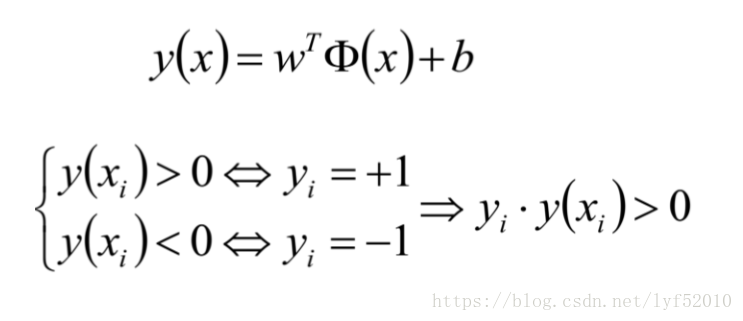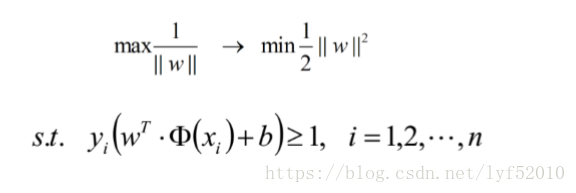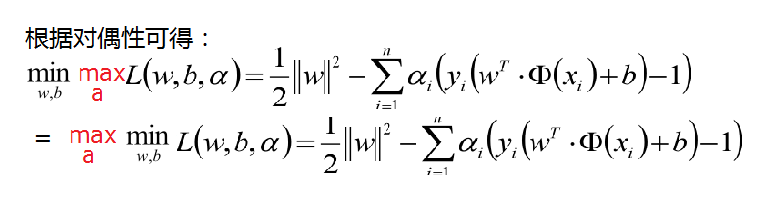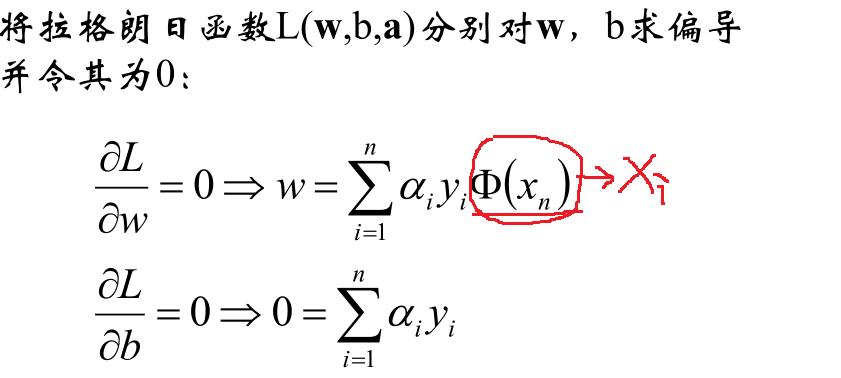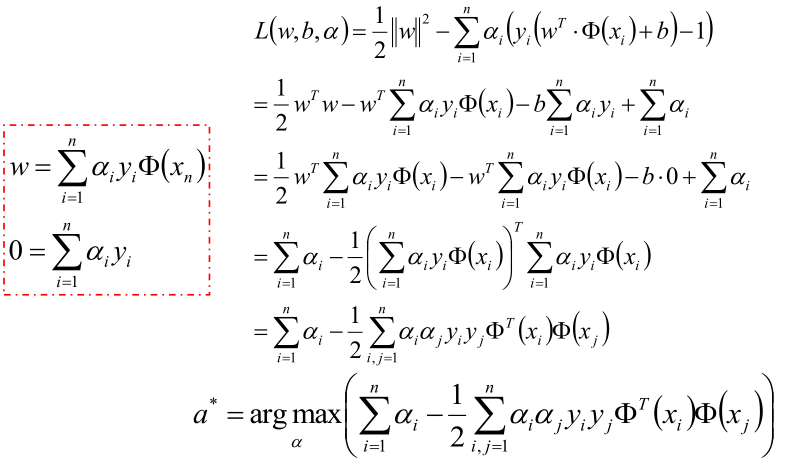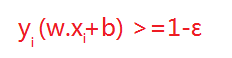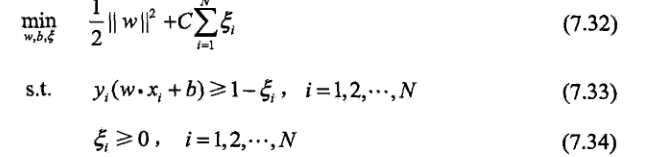机器学习(八)SVM支持向量机

线性分类器：

支持向量

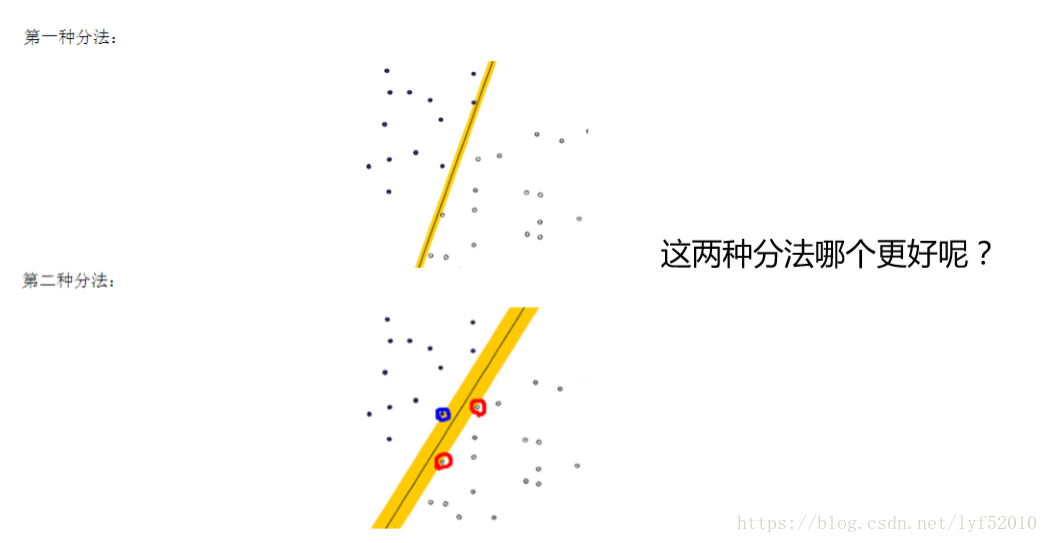
就像我们平时判断一个人是男还是女，就是很难出现分错的情况，这就是男、女两个类别之间的间隙非常的大导致的，让我们可以更准确的进行分类。在SVM 中，称为Maximum Marginal，是SVM的一个理论基础之一。选择使得间隙最大的函数作为分割平面是有很多道理的，比如说从概率的角度上来说，就是使得置信度最小的点置信度最大（听起来很拗口），从实践的角度来说，这样的效果非常好。上图被红色和蓝色的线圈出来的点就是所谓的支持向量(support vector)

线性可分支持向量机

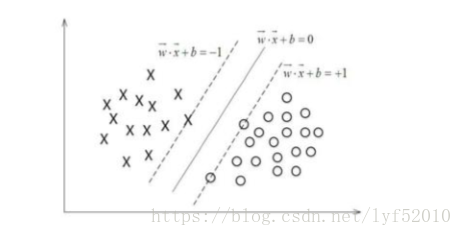
首先我们先假设一条直线为 W•X+b =0 为最优的分割线，把两类分开如下图所示，那我们就要解决的是怎么获取这条最优直线呢?及W 和 b 的值；在SVM中最优分割面(超平面)就是：能使支持向量和超平面最小距离的最大值；

我们的目标是寻找一个超平面，使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面，我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。

在这里假设二维特征向量X=（x1，x2）做另外一个假设就是把b看作是另外一个weight，那么超平面就可以更新为： b+ w1 * x1 +w2 * x2 = 0 所有超平面右上方的点满足： b + w1 * x1 +w2 * x2 > 0 所有超平面左下方的点满足： b+ w1 * x1 +w2 * x2 < 0

数学输入

给定一个特征空间上的训练数据集 T={(x1,y1),(x2,y2),(x3,y3)......(xn,yn)} 其中，x1∈Rⁿ，yi∈{+1,-1},i=1,2,3,4.......N xi为第i个实例(若 n>1,xi为向量) yi为xi的类标记当yi=+1时，称xi为正例当yi=-1时，称xi为负例 (xi,yi)称为样本点

对平面中的点进行等比例缩小或者放大，总有一个比例，使得支持向量点到超平面的距离为1

把w1和w2看成一个向量，x1,x2也是一个向量则有

复习下各种距离欧式距离

https://my.oschina.net/hunglish/blog/787596

最大间隔分离超平面

目标函数

||w||的意思是w的二范数，跟表达式是一个意思，之前得到，求SVM的关键就是，最大化这个式子等价于最小化||w||, 另外由于||w||是一个单调函数，我们可以对其加入平方，和前面的系数。

拉格朗日乘子法

拉格朗日乘子法是一种寻找有等式约束条件的函数的最优值(最大或者最小)的最优化方法.在求取函数最优值的过程中,约束条件通常会给求取最优值带来困难,而拉格朗日乘子法就是解决这类问题的一种强有力的工具.

参考:https://blog.csdn.net/lijil168/article/details/69395023

链接：https://blog.csdn.net/lmm6895071/article/details/78329045?locationNum=7&fps=1

1.3 不等式约束问题（KTT条件）

不等式约束问题：

min f (x) s . t . g (x) = 0 h (x) < = 0

引入拉格朗日函数：(KTT 条件)

L (x, a, b) = f (x) + a g (x) + b h (x) s . t . g (x) = 0 b h (x) = 0

这样就将不等式约束变成了等式约束，偏导等于零即可求得最优参数；

min f (x) 等 价 于 min x max a, b L (x, a, b)

对偶变换后有：

max a, b min L (x, a, b)

因为 h(x)<0h(x)<0 ，所以只有当 bh(x)=0bh(x)=0 时， L(x,a,b)L(x,a,b) 才能取得最大值；否则不满足条件；所以KTT条件是 minf(x)minf(x) 的必要条件；

结合上面的一度的对偶说明故我们的优化函数如下面，其中a >0

现在的优化方案到上面了，先求最小值，对 w 和 b 分别求偏导可以获取如下公式：

把上式获取的参数代入公式优化max值：

化解到最后一步，就可以获取最优的a值：

以上就可以获取超平面！

但在正常情况下可能存在一些特异点，将这些特异点去掉后，剩下的大部分点都能线性可分的，有些点线性不可以分，意味着此点的函数距离不是大于等于1，而是小于1的，为了解决这个问题,提高泛化能力，我们引进了松弛变量 ε>=0; 这样约束条件就会变成为：

故原先的优化函数变为：

对加入松弛变量后有几点说明如下图所以；距离小于1的样本点离超平面的距离为d ,在绿线和超平面之间的样本点都是由损失的，

C越大，惩罚越多，松弛因子越小，越趋近于原函数，有可能过拟合

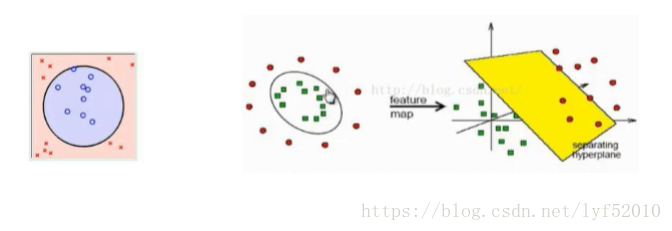
核函数

核函数Kernel 事实上，大部分时候数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在。在上文中，我们已经了解到了SVM处理线性可分的情况，那对于非线性的数据 SVM如何处理呢？对于非线性的情况，SVM 的处理方法是选择一个核函数 κ，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。具体来说，在线性不可分的情况下，支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开。