一、什么是支持向量机SVM

支持向量机（support vector machine），是一种分类算法

假设我们有这样的一堆样本 $D = \left \{(x_{1}, y_{1}), (x_{2}, y_{2}), ..., (x_{n}, y_{n}) \right \},y \in \left \{-1, +1 \right \}$ ，其中y表示不同的类型，这些样本在坐标系中的分布如下：

现在想要使用一个超平面（二维中是直线，一维中是一个数字）把这两种样本进行区分，此时有无数条直线可以做到这件事情，但是在上图的三条直线中，红色的鲁棒性最好，因为两条蓝色的直线，都过于接近两个样本，导致在非训练样本中，如果稍有偏差，就会导致判定错误

SVM要做的事情，就是求得鲁棒性最好的那个超平面

二、数学推导

凸优化问题的转换过程

首先我们知道，点到超平面的距离公式为：

$d = \frac {|w^{T}x + b|}{||w||_{2}}$

其中：

分子为超平面的表达式： $w^{T}x + b$

分母 $||w||_{2}$ 为w向量的二范数，详见：【笔记】向量和矩阵的0、1、2、无穷、p、f、核范数

这个公式在二维的表现形式为点到直线的距离公式：

$d = \frac {|ax_{0} + by_{0} + c|}{\sqrt{a^{2} + b^{2}}}$

假设超平面 $w^{T}x + b$ 能够将样本集D正确分类，即对于 $(x_{i}, y_{i}) \in D$ ，如果 $y_{i} = +1$ ，则 $w^{T}x + b > 0$ ；如果 $y_{i} = -1$ ，则 $w^{T}x + b < 0$ ，则可以表示为：

$f(x) = sign(w, b) = \left\{\begin{matrix} w^{T}x_{i} + b > 0 & y_{i} = +1\\ w^{T}x_{i} + b < 0 & y_{i} = -1 \end{matrix}\right.$

我们先将其进行转换：

对于第一个式子，因为 $w^{T}x + b > 0$ ，所以一定 $\exists \ \lambda > 0$ ，使得 $w^{T}x + b \geqslant \lambda$ 成立，对式子两边同时除 $\lambda$ 得到：

$\frac {w^{T}}{\lambda}x + \frac {b}{\lambda} \geqslant 1$

令新的 $w^{T'} = \frac {w^{T}}{\lambda},, b' = \frac {b}{\lambda }$ ，则新的式子为： $w^{T'}x + b' \geqslant 1$ ，同理可以转换第二个式子，最终原符号函数可以转换为：

$f(x) = sign(w, b) = \left\{\begin{matrix} w^{T}x_{i} + b \geqslant 1 & y_{i} = +1\\ w^{T}x_{i} + b \leqslant -1 & y_{i} = -1 \end{matrix}\right.$

又因为 $y \in \left \{-1, +1 \right \}$ 且与 $w^{T}x_{i} + b$ 同号，所以上述式子继续简化可以写为： $y_{i}(w^{T}x_{i} + b) \geqslant 1 \Rightarrow 1 - y_{i}(w^{T}x_{i} + b) \leqslant 0$

至于为什么要转换为1，个人理解有两个原因：

简化运算

引出soft margin软间隔的理念及损失函数

由第一章的图，我们知道，SVM其实是求的一条直线（其实是超平面，但是说直线更直观一点），满足距离两种类型的点的最小距离最大。其中，最小是指两种类型的点距离直线最近的点，最大是指尽量让直线在两个最近点的中间，以便让鲁棒性能最佳，所以我们要求的其实是：

$\underset{w,b}{max}\ \underset{x}{min} \frac {|w^{T}x + b|}{||w||}$

由我们上面转换的式子可以看出， $|w^{T}x + b| \geqslant 1$ ，所以我们知道上式分子的最小值为1，将min脱掉，可以得到下面的式子以及约束条件：

$\\\underset{w, b}{max}\frac {1}{||w||} \\\\ s.t. \ \ 1 - y_{i}(w^{T}x_{i} + b) \leqslant 0$

其中，第一个式子为要求解的式子，第二个式子为约束条件

对于求 $\frac {1}{||w||}$ 的最大值，等价于求 $||w||$ 的最小值，又因为 $||w|| > 0$ ，所以又等价与求 $||w||^{2}$ 的最小值

这样，我们就将问题转换为了一个凸优化问题，而对于凸优化，转换后的式子如下：

$\\\underset{w, b}{min}\ \frac {1}{2}||w||^{2} = \underset{w, b}{min}\ \frac {1}{2}w^{T}w\\\\ s.t. \ \ 1 - y_{i}(w^{T}x_{i} + b) \leqslant 0\ ,\ i = 1, 2, ..., N$

其中加 $\frac {1}{2}$ 的目的是为了求导时消去2，与BP的均方差前面加 $\frac {1}{2}$ 的目的相同

拉格朗日对偶问题的转换过程

上面我们将问题转换为了带约束条件的凸优化问题。对于此类问题，我们可以用拉格朗日乘子法以及拉格朗日对偶性去求最优解，这里我们只借用结论，不去证明。简单说明如下：

假设我们要求最优解的问题如下：

$\\z = f(x)\\ s.t.\ \ g(x) \leqslant 0, h(x) = 0$

则引入拉格朗日乘子，将式子转换为：

$L(x, \lambda, \alpha) = f(x) + \lambda g(x) + \alpha h(x)$

则此时 $\underset{x}{min}\ \underset{\lambda, \alpha}{max}\ L(x, \lambda, \alpha)$ 与原始最优化问题等价，即具有相同解

而其对偶问题，如果是弱对偶问题，则满足：

$\underset{\lambda, \alpha}{max}\ \underset{x}{min}\ L(x, \lambda, \alpha) \leqslant \underset{x}{min}\ \underset{\lambda, \alpha}{max}\ L(x, \lambda, \alpha)$

如果是强对偶问题，则满足：

$\underset{\lambda, \alpha}{max}\ \underset{x}{min}\ L(x, \lambda, \alpha) = \underset{x}{min}\ \underset{\lambda, \alpha}{max}\ L(x, \lambda, \alpha)$

并满足KKT条件：

$\\g(x) \leqslant 0\\\\ \lambda \geqslant 0\\\\ \lambda g(x) = 0\\\\ h(x) = 0$

将此结论用于当前要求解的式子，可以进行如下转换：

$\left\{\begin{matrix} \underset{w, b}{min}\ \frac {1}{2}w^{T}w\\ s.t. \ \ 1 - y_{i}(w^{T}x_{i} + b) \leqslant 0 \ ,\ i = 1, 2, ..., N \end{matrix}\right. \\\\\\ \Rightarrow \underset{w, b}{min}\ \underset{\lambda}{max}L(w, b, \lambda) = \underset{w, b}{min}\ \underset{\lambda}{max}[\frac {1}{2}w^{T}w + \sum _{i = 1}^{N}\lambda _{i}(1 - y_{i}(w^{T}x_{i} + b))] \\\\ = \underset{w, b}{min}\ \underset{\lambda}{max}[\frac {1}{2}w^{T}w + \sum _{i = 1}^{N}(\lambda_{i} - \lambda _{i}y_{i}(w^{T}x_{i} + b))]\\\\ = \underset{w, b}{min}\ \underset{\lambda}{max}[\frac {1}{2}w^{T}w + \sum _{i = 1}^{N}\lambda_{i} - \sum _{i = 1}^{N}\lambda_{i}y_{i}w^{T}x_{i} - \sum _{i = 1}^{N}\lambda_{i}y_{i}b]$

因为原式子其实是N个约束条件，所以这里要添加一个求和公式。对于当前的式子，因为是凸二次优化问题 + 线性约束条件，所以其满足强对偶关系，转换为其对偶表达式，并添加KKT条件，得到下面的式子：

$\\\underset{\lambda}{max}\ \underset{w, b}{min}\ [\frac {1}{2}w^{T}w + \sum _{i = 1}^{N}\lambda_{i} - \sum _{i = 1}^{N}\lambda_{i}y_{i}w^{T}x_{i} - \sum _{i = 1}^{N}\lambda_{i}y_{i}b]\\\\ \lambda_{i} \geqslant 0\\\\ 1 - y_{i}(w^{T}x_{i} + b) \leqslant 0\\\\ \lambda (1 - y_{i}(w^{T}x_{i} + b)) = 0$

求导过程

根据上述式子，先对b求导可得：

$\frac {\partial L}{\partial b} = \frac {\partial }{\partial b}[\frac {1}{2}w^{T}w + \sum _{i = 1}^{N}\lambda_{i} - \sum _{i = 1}^{N}\lambda_{i}y_{i}w^{T}x_{i} - \sum _{i = 1}^{N}\lambda_{i}y_{i}b]= -\sum _{i = 1}^{N}\lambda_{i}y_{i} = 0$

将此结果带入到原式，可将最后一项消掉，转换为：

$\underset{\lambda}{max}\ \underset{w, b}{min}\ [\frac {1}{2}w^{T}w + \sum _{i = 1}^{N}\lambda_{i} - \sum _{i = 1}^{N}\lambda_{i}y_{i}w^{T}x_{i}]$

因为最后一项的b与i没有关系，所以可以将b提出来，然后b * 0 = 0，将最后一项消掉

但是倒数第二项中的x是与i相关的，所以不可以消掉

再对w求导可得：

$\frac {\partial}{\partial w}[\frac {1}{2}w^{T}w + \sum _{i = 1}^{N}\lambda_{i} - \sum _{i = 1}^{N}\lambda_{i}y_{i}w^{T}x_{i}] = w - \sum _{i = 1}^{N}\lambda_{i}y_{i}x_{i} = 0\\\\ \therefore w = \sum _{i = 1}^{N}\lambda_{i}y_{i}x_{i}$

将w的表达式带入到原式中，可得：

$\underset{\lambda}{max}\ \underset{w, b}{min}\ [\frac {1}{2}w^{T}w + \sum _{i = 1}^{N}\lambda_{i} - \sum _{i = 1}^{N}\lambda_{i}y_{i}w^{T}x_{i}] \\\\= \underset{\lambda}{max}[\frac {1}{2}(\sum _{i = 1}^{N}\lambda_{i}y_{i}x_{i})^{T}(\sum _{j = 1}^{N}\lambda_{j}y_{j}x_{j})] - \sum _{i = 1}^{N}\lambda_{i}y_{i}(\sum _{j = 1}^{N}\lambda_{j}y_{j}x_{j})^{T}x_{i} + \sum _{i = 1}^{N}\lambda_{i}$

因为 $\lambda_{i}, \lambda_{j}, y_{i}, y_{j}$ 均为常量，所以转置等于自己

而 $x_{i}^{T}x_{j} = x_{j}^{T}x_{i}$ 均为常量，所以上式转换为：

$\underset{\lambda}{max}[\frac {1}{2}\sum _{i = 1}^{N}\sum _{j = 1}^{N}\lambda_{i}\lambda_{j}y_{i}y_{j}x_{i}^{T}x_{j} - \sum _{i = 1}^{N}\sum _{j = 1}^{N}\lambda_{i}\lambda_{j}y_{i}y_{j}x_{i}^{T}x_{j} + \sum _{i = 1}^{N} \lambda_{i}] \\\\= \underset{\lambda}{max}[-\frac {1}{2}\sum _{i = 1}^{N}\sum _{j = 1}^{N}\lambda_{i}\lambda_{j}y_{i}y_{j}x_{i}^{T}x_{j} + \sum _{i = 1}^{N} \lambda_{i}]$

所以最终转换的结果和约束条件为：

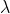
$\underset{\lambda}{max}[-\frac {1}{2}\sum _{i = 1}^{N}\sum _{j = 1}^{N}\lambda_{i}\lambda_{j}y_{i}y_{j}x_{i}^{T}x_{j} + \sum _{i = 1}^{N} \lambda_{i}]\\\\ s.t. \ \ \sum _{i = 1}^{N}\lambda_{i}y_{i} = 0, \lambda_{i} \geqslant 0$

超平面方程为：

$f(x) = w^{T}x + b = (\sum _{i = 1}^{N}\lambda _{i}y_{i}x_{i})^{T}x + b = \sum _{i = 1}^{N}\lambda _{i}y_{i}x_{i}^{T}x + b$

SMO求解 $\lambda$

上述式子转换完成后，唯一的未知变量为 $\lambda$ ，如何求得 $\lambda$ 的最优值呢，有个常用的算法为SMO算法，主要利用了限制条件 $\sum _{i = 1}^{N}\lambda_{i}y_{i} = 0$ ，它的基本思路为：

选取一堆需要更新的 $\lambda_{i}, \lambda _{j}$

固定 $\lambda_{i}, \lambda _{j}$ 以外的参数，求解 $\underset{\lambda}{max}[-\frac {1}{2}\sum _{i = 1}^{N}\sum _{j = 1}^{N}\lambda_{i}\lambda_{j}y_{i}y_{j}x_{i}^{T}x_{j} + \sum _{i = 1}^{N} \lambda_{i}]$ ，并获得更新后的 $\lambda_{i}, \lambda _{j}$

因为我们有KKT条件，所以只需要选取的 $\lambda_{i}, \lambda _{j}$ 有一个不满足KKT条件，目标函数就回在迭代后增大，并且违背的程度越大，目标函数值得增幅也就越大（可参考KKT的推导过程）。所以，SMO先选取违背KKT条件程度最大的变量，第二个变量应选择一个使目标函数值增长最快的变量，单由于比较各变量所对应的目标函数值增幅的复杂度过高，所以SMP采用了一个启发式：使选取的两变量所对应样本之间的间隔最大。这样的两个变量有很大的差别，与对两个相似的变量进行更新相比，对他们进行更新会给目标函数值带来更大的变化

三、结论

要求最优解的最终式子及约束条件为：

$\underset{\lambda}{max}[-\frac {1}{2}\sum _{i = 1}^{N}\sum _{j = 1}^{N}\lambda_{i}\lambda_{j}y_{i}y_{j}x_{i}^{T}x_{j} + \sum _{i = 1}^{N} \lambda_{i}]\\\\ s.t. \ \ \sum _{i = 1}^{N}\lambda_{i}y_{i} = 0, \lambda_{i} \geqslant 0$

超平面方程为：