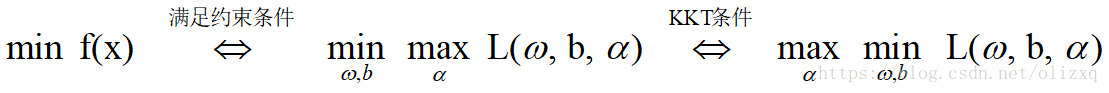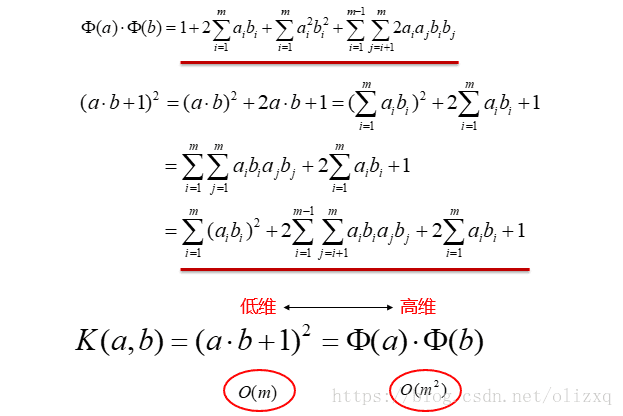机器学习：支持向量机（SVM）

支持向量机(SVM)是一种二类分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机。支持向量机还可以引入核技巧，使其成为实质上的非线性分类器。支持向量机的学习算法是求解凸二次规划的最优化算法。
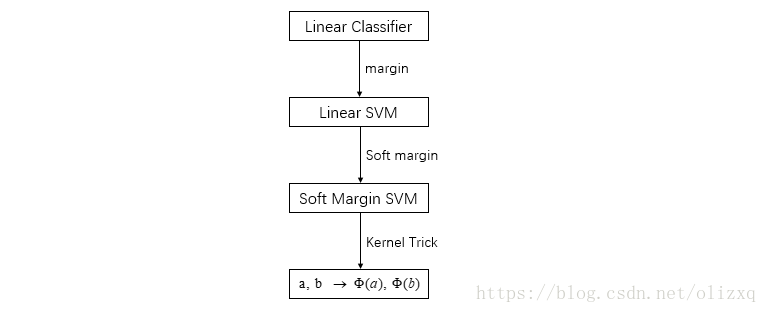
SVM的演变过程如下所示：

本文的内容包括：
1、SVM的推导过程
2、非线性支持向量机和核函数
3、序列最小最优化算法(SMO)
4、简单实现

1、SVM的推导过程

线性支持向量机将输入空间中的输入映射为特征空间中的特征向量，非线性支持向量机利用一个从输入空间到特征空间的非线性映射将输入映射为特征向量，支持向量机的学习是在特征空间进行的。

线性可分支持向量机利用间隔最大化求最优分类超平面，此时，分类超平面是唯一的。

线性支持向量机的目标是通过给定的数据集，求出分离超平面：
$\omega^*·x+b^*=0$
相应的分类决策函数为：
$f(x) = sign(\omega^*·x+b^*)$

下面来看如何得到这样的分类超平面和分类决策函数，具体推导过程从这里开始：

1.1 定义分类间隔

首先要使得分类间隔最大化，那就需要先定义这个间隔：因为在超平面 $\omega·x+b=0$确定的情况下， $|\omega·x+b|$可以表示点 $x$距离超平面的远近，而预测结果 $\omega·x+b$的符号和类标记y的符号是否一致可以表示分类是否正确，于是用 $y(\omega·x+b)$表示分类的正确性和确信度，定义为函数间隔。

定义好分类的间隔，于是，样本点 $(x_i,y_i)$关于超平面 $(\omega,b)$的函数间隔为：
$\hat \gamma_i = y_i(\omega·x_i+b)$
既然我们要使得分类间隔最大化，那么只要使最坏情况下的函数间隔最大化（让间隔最小的点的间隔最大化）：
$\hat \gamma = \min_{i=1,...,N} \hat \gamma_i$
此时我们只需要 $max \; \hat \gamma$求出此时的 $(\omega,b)$即可。

但是这里存在一个问题，由 $\hat \gamma$的定义可知，当 $\omega$和 $b$同时放大相同的倍数， $\hat \gamma$可以达到任意大的数，但分离超平面并没有改变，这说明函数间隔无法确定唯一的 $\omega$和 $b$。

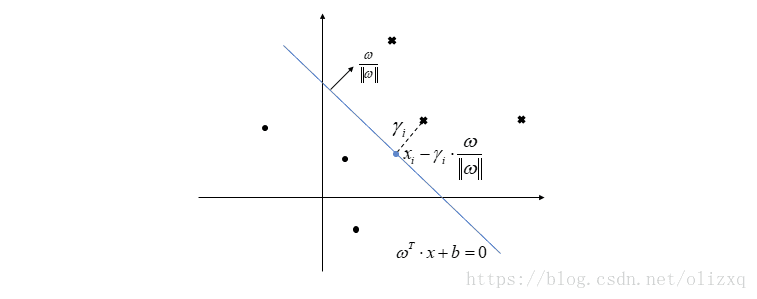
此时我们应该怎么办呢？既然函数间隔不能使用的原因是 $\omega$和 $b$可以随意变化，那么我们可以考虑定义一个样本点到超平面的几何距离，这样便可唯一确定超平面，如下图。

现在我们定义几何间隔，该间隔是样本点到超平面的几何距离，由上图，将分离超平面上的点带入方程得到：
$\omega^T(x_i-\gamma_i{\omega\over {||\omega||}})+b = 0$
从而得到：
$\gamma_i = {\omega^T\over {||\omega||}}·x_i + {b\over {||\omega||}}$
如果在负的一侧：
$\gamma_i = -({\omega^T\over {||\omega||}}·x_i + {b\over {||\omega||}})$

因此得到 $x_i$与超平面 $(\omega,b)$的几何间隔为：
$\gamma_i = y_i({\omega^T\over {||\omega||}}·x_i + {b\over {||\omega||}})$

同前面一样，要使最坏情况下的几何间隔最大化：
$\gamma = \min_{i=1,...,N} \gamma_i$
此时我们只需要 $max \; \gamma$求出此时的 $(\omega,b)$即可。

其中：几何间隔与函数间隔的关系 $\gamma = {\hat \gamma \over {||\omega||}}$；

1.2 有约束的最优化问题

于是我们得到有约束的最优化问题：
$\max_{\omega,b} \quad \gamma\\ s.t. \quad y_i({\omega^T\over {||\omega||}}·x_i + {b\over {||\omega||}}) \ge \gamma, \quad i=1,2,...,N$

根据几何间隔与函数间隔的关系，上式可写为：
$\max_{\omega,b} \quad {\hat \gamma \over {||\omega||}}\\ s.t. \quad y_i({\omega^T}·x_i + {b}) \ge \hat \gamma, \quad i=1,2,...,N$

由于任意改变 $\omega$和 $b$，转化为 $\lambda\omega$和 $\lambda b$，此时函数间隔成为 $\lambda \hat \gamma$，对约束条件没有影响，对优化的目标函数也没有影响，不妨取 $\hat \gamma = 1$，由于最大化 ${1 \over {||\omega||}}$和最小化 ${1 \over 2} ||\omega||^2$是等价的，于是得到最优化问题：
$\min_{\omega,b} \quad {1 \over 2} ||\omega||^2\\ s.t. \quad y_i({\omega^T}·x_i + {b}) - 1 \ge 0, \quad i=1,2,...,N$
这是一个凸二次规划问题，因此可以 使用二次规划的优化计算包求解，但是当数据量很大时，很难去求解，于是我们需要去找到更加高效的解决办法。

1.3 从原始问题到对偶问题

考虑到拉格朗日乘数法可以解决有约束的极值问题，因此该优化问题的拉格朗日函数为：
$L(\omega, b, \alpha) = {1\over 2}||\omega||^2-\sum^n_{i=1}\alpha_iy_i(\omega x_i + b) + \sum^n_{i=1}\alpha_i$

为什么拉格朗日函数可以求解有约束的极值问题？
对于有约束的优化问题：
$min \; f(x)$
$s.t. \; c_i(x) \le 0, \quad i=1,2,...,k$
$h_j(x) = 0, \quad j=1,2,...,l$
拉格朗日函数如下：
$L(x, \omega, \beta) = f(x)-\sum^k_{i=1}\alpha_ic_i(x) + \sum^l_{i=1}\beta_jh_j(x), \; \alpha_i \ge 0$
令 $\theta_P(x) = \max_{\alpha,\beta:\alpha \ge 0}L(x, \alpha, \beta)$
对上式的解释：
如果 $c_i(x) \gt 0$，那么 $\theta_P(x) = \infty$
如果 $h_j(x) \ne 0$，那么 $\theta_P(x) = \infty$
否则， $\theta_P(x) = f(x)$
因此，
$\theta_P(x)= \begin{cases} f(x), & \text {x满足原始问题约束} \\ +\infty, & \text{其它} \end{cases}$
所以，在x满足原始问题约束时， $f(x)$与 $\theta_P(x)$等价：
$min \; f(x) = min \; \theta_P(x)$
故：原始优化问题可以转化为:
$min \; \theta_P(x) = \min_x \; \max_{\alpha,\beta:\alpha \ge 0} L(x, \alpha, \beta)$
$\;$
对其对偶问题： $\theta_D(x) = \min_{x} L(x, \alpha, \beta)$
$\max_{\alpha,\beta:\alpha \ge 0} \theta_D(\alpha, \beta) = \max_{\alpha,\beta:\alpha \ge 0} \; \min_x L(x, \alpha, \beta)$
从而得到对偶问题：
$\max_{\alpha,\beta} \theta_D(\alpha, \beta) = \max_{\alpha,\beta} \; \min_x L(x, \alpha, \beta)$
$s.t. \; \alpha_i \ge 0, \quad i=1,2,...,k$
$\;$
由于：
$\min_x \; \max_{\alpha,\beta:\alpha \ge 0} L(x, \alpha, \beta) \ge \max_{\alpha,\beta} \; \min_x L(x, \alpha, \beta)$
在满足KKT条件时，等号成立。

通过上面的分析，对原始问题可以得到如下等价条件：

KKT条件：
$∇_aL(\omega^∗,b^∗,\alpha^∗)=0,∇_{\omega}L(\omega^∗,b^∗,\alpha^∗)=0,∇_bL(\omega^∗,b^∗,\alpha^∗)=0;\\ \alpha_i^∗⋅(y_i({\omega^T}^∗·x_i + {b}^∗) - 1)=0;\\ y_i({\omega^T}^∗·x_i + {b}^∗) - 1 \ge 0;\\ \alpha_i^∗≥0$

因此原优化问题可以转化对偶问题求解为：
$\max_{\alpha} \; \min_{\omega, b} L(\omega, b, \alpha)$

化为对偶问题的原因：
（1）使用SMO算法；
（2）转化为内积的形式，使用核函数，映射到高维空间，进行非线性分类。

1.4 求解得到对偶最优化问题

因此，该问题分成两步求解：

（1）求 $\min_{\omega, b} L(\omega, b, \alpha)$
$∇_{\omega}L(\omega,b,\alpha)=\omega - \sum^N_{i=1}\alpha_iy_ix_i=0\\ ∇_bL(\omega,b,\alpha)=-\sum^n_{i=1}\alpha_iy_i=0$
从而得到：
$\omega = \sum^N_{i=1}\alpha_iy_ix_i\\ \sum^n_{i=1}\alpha_iy_i=0$
代入拉格朗日函数：
$\min_{\omega, b} L(\omega, b, \alpha) = -{1\over 2}\sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_jy_iy_j(x_ix_j) + \sum^n_{i=1}\alpha_i$

（2）对 $\min_{\omega, b} L(\omega, b, \alpha)$求极大值，得到：
$\max_{\alpha} \; -{1\over 2}\sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_jy_iy_j(x_ix_j) + \sum^n_{i=1}\alpha_i\\ s.t. \; \sum^n_{i=1}\alpha_iy_i=0\\ \alpha_i \ge 0, \quad i = 1,2,...,N$
转化为求极小，得到对偶最优化问题：
$\min_{\alpha} \; {1\over 2}\sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_jy_iy_j(x_ix_j) - \sum^n_{i=1}\alpha_i\\ s.t. \; \sum^n_{i=1}\alpha_iy_i=0\\ \alpha_i \ge 0, \quad i = 1,2,...,N$
由上式求得对偶最优化问题的解：
$\alpha^* = (\alpha^*_1,\alpha^*_2,...,\alpha^*_l)^T, \; 存在j，使得\alpha^*_j \gt 0$
由（1）中可知：
${\omega^T}^∗ = \sum^N_{i=1}\alpha_iy_ix_i$
由KKT条件：
$\alpha_i^∗⋅(y_i({\omega^T}^∗·x_i + {b}^∗) - 1)=0$
因为至少有一个 $\alpha_j^∗ \gt 0$（原因《统计学习方法》有解释），所以：
$y_j({\omega^T}^∗·x_j + {b}^∗) - 1=0$
得到：
$b^* = y_j - {\omega^T}^∗·x_j= y_j - \sum^N_{i=1}\alpha_i^*y_i(x_i·x_j)$
所以，分离超平面为：
$\sum^N_{i=1}\alpha_i^*y_i(x_i·x_j) + b^* = 0$
分类决策函数为：
$f(x) = sign(\sum^N_{i=1}\alpha_i^*y_i(x_i·x_j) + b^*)$

从而得到线性可分支持向量机的学习算法：

1.5 线性不可分的线性支持向量机

对于线性不可分的问题，对每个样本点 $(x_i,y_i)$引入一个松弛变量 $\xi_i \ge 0$，使函数间隔加上松弛变量大于等于1。这样约束条件变为：
$y_i(\omega·x_i+b) \ge 1 - \xi_i$
同时，为每个松弛变量 $\xi_i$，支付一个代价 $\xi_i$。目标函数由原来的 ${1\over 2}||\omega||^2$变成：
${1\over 2}||\omega||^2 + C\sum^N_{i=1}\xi_i$
其中，C>0为惩罚参数（C越大，惩罚越大，越不希望看到离群点）。

因此，线性不可分的线性支持向量机的原始问题为：
$\min_{\omega, b, \xi} \; {1\over 2}||\omega||^2 + C\sum^N_{i=1}\xi_i\\ s.t. \; y_i(\omega·x_i + b) \ge 1-\xi_i, \quad i=1,2,...,N\\ \xi_i \ge 0, \quad i=1,2,...,N$
后续推导方式同线性可分支持向量机类似，得到：

2、非线性支持向量机和核函数

用线性问题解决非线性问题可以分成两步：
（1）首先使用一个变换将原空间的数据映射到新空间；
（2）在新空间里用线性分类学习方法从训练数据中学习分类模型。

2.1 核技巧的基本思想：

通过一个非线性变换将输入空间对应于一个特征空间，使得在输入空间中的超曲面模型对应与特征空间中的超平面模型，这样，分类任务通过在特征空间中求解线性支持向量机就可以完成。

2.2 核函数：

如果存在一个从输入空间 $X$到特征空间 $H$的映射：
$\phi(x): X \rightarrow H$
使得对所有 $x, z \in X$，函数 $K(x,z)$满足条件：
$K(x,z)=\phi(x)·\phi(z)$
则称 $K(x,z)$为核函数， $\phi(x)$为映射函数，式中 $\phi(x)·\phi(z)$为 $\phi(x)$和 $\phi(z)$的内积。

核技巧的想法是，在学习和预测中只定义核函数 $K(x,z)$，而不显式地定义映射函数 $\phi$，使得 $K(x,z)$的计算结果与 $\phi(x)$和 $\phi(z)$在高维的内积结果相同，从而使在低维的运算等价于在高维的操作。

2.3 核技巧的应用：

由于在线性支持向量机中，无论是目标函数还是决策函数都只涉及输入实例与实例之间的内积，因此内积 $x_i·x_j$可以用核函数 $K(x_i, x_j) = \phi(x_i)·\phi(x_j)$来代替，得到：
$W(\alpha) = {1\over 2}\sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_jy_iy_j(x_ix_j) - \sum^n_{i=1}\alpha_i$

经过映射函数 $\phi$将原来的输入空间变换到一个新的特征空间，将输入空间中的内积 $x_i·x_j$变换为特征空间中的内积 $\phi(x_i)·\phi(x_j)$，在新的特征空间里从训练样本中学习线性支持向量机。

在核函数 $K(x,z)$给定的条件下，可以利用解线性分类问题的方法求解非线性分类问题的支持向量机。学习是隐式地在特征空间进行的，不需要显式地定义特征空间和映射函数。

2.4 常用的核函数：

（1）多项式核函数：
$K(x,z) = (x·z + 1)^p$
对应的是p次多项式分类器，分类决策函数是：
$f(x) = sign(\sum^{N_s}_{i=1}a^*_iy_i(x_i·x+1)^p+b^*)$
（2）高斯核函数
$K(x,z) = exp(-{||x-z||^2 \over 2\sigma^2})$
对应的是高斯径向基函数分类器，分类决策函数是：
$f(x) = sign(\sum^{N_s}_{i=1}a^*_iy_iexp(-{||x-z||^2 \over 2\sigma^2})+b^*)$

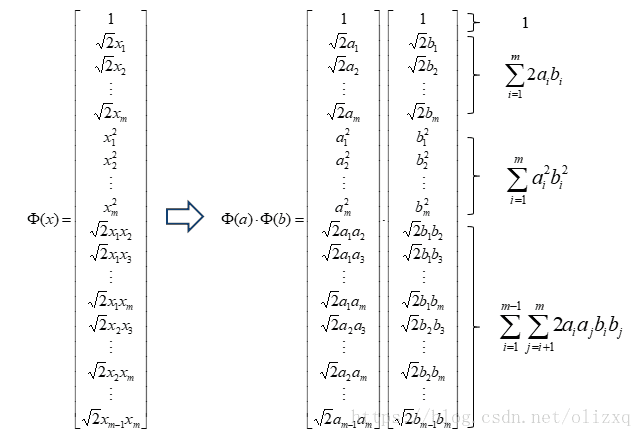
下面从2次多项式来推导核函数的低维运算等价于高维运算的结果：

由核技巧得到非线性支持向量机算法：

3、序列最小最优化算法(SMO)

$\qquad$SMO算法是支持向量机学习的一种快速算法。其特点是不断地将原二次规划问题分解为只有两个变量的二次规划问题（减而治之），并对子问题进行解析求解，直到所有变量满足KKT条件。

$\qquad$具体SMO算法可参见《统计学习方法》和这篇文章，已经很详细了，下面是对该算法的简单实现，最终结果在线性可分数据集上还可以，在eris数据集上只能达到将近70%正确率，sklearn中的SVC可以达到100%，工程上应该是做了很多优化，单纯按照书上的原理实现，最终效果肯定没有工程上广泛使用的算法效果好，但是实现一遍也可以收获很大，SVM的python实现参考了文末给出的博客。

4、简单实现

from numpy import *
from sklearn import datasets, model_selection
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import random
import copy

class SVM:
    """
    初始化SVM相应的值
    X: 输入样本
    y：标签
    b：偏置项
    C：离群点的权重，C越大表明对离群点加的惩罚越大，也就是越不希望看到离群点
    Toler：松弛变量
    maxIter：最大迭代次数
    kernelType：核函数类型
    # 核函数类型：
    # kernelType=("rbf", 1) rbf 表示使用径向基RBF函数作为核函数,其第二个参数不可为0
    # kernelType=("polynomial", 2) polynomial 表示使用多项式函数作为核函数,其第二个参数不可为0
    # kernelType=("linear", 0) linear 表示使用线性函数作为核函数,不会使用到第二个参数
    numSamples：样本个数
    alpha：所有样本的拉格朗日因子
    kernelMat：计算x矩阵的核函数矩阵
    errorCache：每次迭代的误差
    """
    def __init__(self, C, Toler, maxIter, kernelType):
        self.X = None
        self.y = None
        self.b = 0
        self.C = C
        self.Toler = Toler
        self.maxIter = maxIter
        self.kernelType = kernelType
        self.numSamples = 0
        self.alpha = None
        self.kernelMat = None
        self.errorCache = None

    def calcKernelMat(self):
        """
        计算X矩阵的核函数矩阵

        :return:核函数矩阵
        """
        kernelMat = mat(zeros((self.numSamples, self.numSamples)))
        for i in range(self.numSamples):
            kernelMat[:, i] = self.calcKernelValue(self.X, self.X[i, :], self.numSamples)
        return kernelMat

    def calcKernelValue(self, X, xi, numSamples):
        """
        计算每一个样本与所有样本的核函数(按照模型设定核函数的类型计算)

        :param X: 输入样本集
        :param xi: 输入一个样本
        :param numSamples: 样本数量
        :return: 某个样本与所有样本的核函数
        """
        kernelValue = mat(zeros((numSamples, 1)))
        # 选择核函数
        if self.kernelType[0] == "linear":
            kernelValue = X * xi.T
        elif self.kernelType[0] == "polynomial":
            K = X * xi.T
            for j in range(numSamples):
                kernelValue[j] = (K[j] + 1)**self.kernelType[1]
        elif self.kernelType[0] == "rbf":
            sigma = self.kernelType[1]
            if sigma == 0:
                sigma = 1.0
            for j in range(numSamples):
                diff = X[j, :] - xi
                kernelValue[j] = exp(diff * diff.T / (- 2.0 * sigma ** 2))
        else:
            # 通过raise显示地引发异常。一旦执行了raise语句，raise后面的语句将不能执行
            raise NameError('请选择核函数的类型')
        return kernelValue

    def train(self, X, y):
        """
        模型训练

        :return: 模型和迭代次数
        """
        # 设置SVM的内部变量
        self.X = X
        self.y = y
        self.numSamples = X.shape[0]
        self.kernelMat = self.calcKernelMat()
        self.alpha = mat(zeros((self.numSamples, 1)))
        self.errorCache = mat(zeros((self.numSamples, 2)))

        # 记录实际迭代的次数
        iterCount = 0
        # 是否使用全部样本
        entireSet = True
        # 是否对拉格朗日因子进行更新
        isChange = 0

        # 开始迭代,终止条件为：
        # 1、完成所有迭代
        # 2、α的值不再发生变化并且所有α(样本)符合KKT条件
        while (iterCount < self.maxIter) and ((isChange > 0) or entireSet):
            isChange = 0

            # 使用全部样本
            if entireSet:
                for i in range(self.numSamples):
                    isChange += self.innerLoop(i)
                iterCount += 1

            # 使用满足条件0 < αi < C的样本点，即在间隔边界上的支持向量，检验是否满足KKT条件。
            else:
                nonBoundAlphasList = nonzero((self.alpha.A > 0) * (self.alpha.A < svm.C))[0]
                for i in nonBoundAlphasList:
                    isChange += self.innerLoop(i)
                iterCount += 1

            if entireSet:
                entireSet = False
            elif isChange == 0:
                entireSet = True

        print(iterCount)

    def innerLoop(self, i):
        Ei = self.calcError(i)
        # 判断该点是否符合KKT条件，符合就返回寻找下一个不符合KKT的样本点，不符合进行更新
        if self.fitKKT(i):
            return 0

        # 根据αi选择αj
        j, Ej = self.selectAlpha_j(i, Ei)
        alpha_i_old = copy.deepcopy(self.alpha[i])
        alpha_j_old = copy.deepcopy(self.alpha[j])

        # 计算边界L和H
        # if yi!=yj L=max(0,αj-αi) H=min(C,C+αj-αi)
        # if yi==yj L=max(0,αj+αi-C) H=min(C,αj+αi)
        if self.y[i] != self.y[j]:
            L = max(0, self.alpha[j] - self.alpha[j])
            H = min(self.C, self.C + self.alpha[j] - self.alpha[i])
        else:
            L = max(0, self.alpha[j] + self.alpha[i] -self.C)
            H = min(self.C, self.alpha[j] + self.alpha[i])
        # ?
        if L == H:
            return 0

        # 计算样本i和j之间的相似性
        Eta = 2.0 * self.kernelMat[i, j] - self.kernelMat[i, i] - self.kernelMat[j, j]
        if Eta >= 0 :
            return 0

        # 更新αj
        self.alpha[j] -= self.y[j] * (Ei - Ej) / Eta

        # αj必须在边界内，因此在计算出新的αj后要对其进行新的裁剪
        # if αj > H then αj = H
        # if L <= αj <= H then αj = αj
        # if αj < L then αj = L
        if self.alpha[j] > H:
            self.alpha[j] = H
        if self.alpha[j] < L:
            self.alpha[j] = L

        # 如果本次更新几乎没有变化就返回
        if abs(alpha_j_old - self.alpha[j]) < 0.00001:
            return 0

        # 更新αi：αi=αi+yi*yj*(aj_old-aj)
        self.alpha[i] += self.y[i] * self.y[j] * (alpha_j_old - self.alpha[j])

        # 更新阀值b
        # b1=b-Ei-yi(αi-αi_old)<xi,xi>-yj(αj-αj_old)<xi,xj>
        # b2=b-Ej-yi(αi-αi_old)<xi,xj>-yj(αj-αj_old)<xj,xj>
        b1 = self.b - Ei - self.y[i] * (self.alpha[i] - alpha_i_old) * self.kernelMat[i, i] - \
             self.y[j] * (self.alpha[j] - alpha_j_old) * self.kernelMat[i, j]
        b2 = self.b - Ej - self.y[i] * (self.alpha[i] - alpha_i_old) * self.kernelMat[i, j] - \
             self.y[j] * (self.alpha[j] - alpha_j_old) * self.kernelMat[j, j]

        # if 0<αi<C then b=b1
        # if 0<αj<C then b=b2
        # if other then b=(b1+b2)/2
        if 0 < self.alpha[i] < self.C:
            self.b = b1
        elif 0 < self.alpha[j] < self.C:
            self.b = b2
        else:
            self.b = (b1 + b2) / 2.0

        self.updateError(i)
        self.updateError(j)

        return 1

    def updateError(self, i):
        """
        更新样本误差

        :param i: 某个样本行号
        :return: 误差
        """
        E = self.calcError(i)
        self.errorCache[i] = [1, E]

    def calcError(self, i):
        """
        计算样本点的预测误差

        :param i: 某个样本点所在的行
        :return: 误差
        """
        Ei = multiply(self.alpha, self.y).T * self.kernelMat[:, i] + self.b - self.y[i]
        return Ei

    def selectAlpha_j(self, i, Ei):
        """
        选择最优的αj

        :param i: 某个样本行号i
        :param Ei: 样本预测误差
        :return: 样本j, 误差Ej
        """
        self.errorCache[i] = [1, Ei]

        # 找出所有符合KKT条件的乘子的E
        alphaList = nonzero(self.errorCache[:, 0].A)[0]

        maxStep = 0
        j = 0
        Ej = 0

        # 选择误差步长最大的最为αj
        if(len(alphaList) > 1):
            for k in alphaList:
                if k == i:
                    continue
                Ek = self.calcError(k)
                if abs(Ei - Ek) > maxStep:
                    maxStep = abs(Ei - Ek)
                    j = k
                    Ej = Ek
        # 如果是第一次，随机选择αj
        else:
            j = i
            while j == i:
                j = random.randint(0, self.numSamples - 1)
            Ej = self.calcError(j)
        return j, Ej


    def fitKKT(self, i):
        """
        判断是否符合KKT条件

        :param i: 某个样本行号
        :return: 是否符合KKT条件（1：符合，0：不符合）
        """
        E = self.calcError(i)
        # 约束条件1：0<=α<=C
        # 约束条件2：必须满足KKT条件
        #     1-1、if yf>=1 then α==0
        #     1-2、if yf<=1 then α==C
        #     1-3、if yf==1 then 0<α<C
        #     因此可以得到不满足KKT的条件
        #     2-1、if yf>=1 then α>0
        #     2-2、if yf<=1 then α<C
        #     2-3、if yf==1 then α==0 or α==C
        #     仔细考虑2-1，当yf=1 then α>0,符合1-3
        #     仔细考虑2-1，当yf=1 then α<C,符合1-3
        #     仔细考虑2-3，符合1-1和1-2
        #     因此得到：
        #     3-1、if yf>1 then α>0
        #     3-2、if yf<1 then α<C
        #     预测值与真实值之差 E=f-y
        #     yE=yf-yy because y∈(-1,1) so yE=fy-1
        #     4-1、if yE>0 then α>0
        #     4-2、if yE<0 then α<C
        #     我们在这里加入一个松弛变量Toler：
        #     1、if yE>Toler then α>0
        #     2、if yE<-Toler then α<C
        if self.y[i] * E < -self.Toler and self.alpha[i] < self.C or self.y[i] * E > self.Toler and self.alpha[i] > 0:
            return 0
        else:
            return 1

    def predict(self, x):
        """
        模型预测

        :param x: 测试数据
        :return: 预测分类结果
        """
        n = x.shape[0]
        # 加入核函数之后，新的fx=yi*ai*k<x,xi>+b
        # 又因为alphas大多数都为0，因此值用计算不为0的就可以
        supportVectorsIndex = nonzero((self.alpha.A > 0) * (self.alpha.A < self.C))[0]
        supportVectors = self.X[supportVectorsIndex]
        # print(supportVectors)
        supportVectorLabels = self.y[supportVectorsIndex]
        supportVectorAlphas = self.alpha[supportVectorsIndex]
        predict = array(zeros((n, 1)))
        for i in range(n):
            kernelValue = self.calcKernelValue(supportVectors, x[i, :], len(supportVectors))
            predict[i] = kernelValue.T * multiply(supportVectorLabels, supportVectorAlphas) + self.b
        return predict


    def score(self, x, y):
        """
        预测准确率

        :param x: 测试样本
        :param y: 测试集标签
        :return: 准确率
        """
        n = x.shape[0]
        predict = self.predict(x)
        matchCount = 0
        for i in range(n):
            if sign(predict[i]) == sign(y[i]):
                matchCount += 1
        accuracy = float(matchCount) / n
        return accuracy

"""
# 对于二分类任务的可视化结果(data.txt)
def draw(model):
    # 画出所有的点
    for i in range(model.numSamples):
        if model.y[i] == -1:
            plt.plot(model.X[i, 0], model.X[i, 1], 'or')
        elif model.y[i] == 1:
            plt.plot(model.X[i, 0], model.X[i, 1], 'ob')

    # 画出支持向量
    supportVectorsIndex = nonzero(
        (model.alpha.A > 0) * (model.alpha.A < model.C))[0]
    for i in supportVectorsIndex:
        plt.plot(model.X[i, 0], model.X[i, 1], 'oy')


    w = zeros((2, 1))
    # 求wi=yi*ai*xi i=0,1,2...n
    for i in supportVectorsIndex:
        w += multiply(model.alpha[i] * model.y[i], model.X[i, :].T)
    min_x = min(model.X[:, 0])[0, 0]
    max_x = max(model.X[:, 0])[0, 0]
    y_min_x = float(- model.b - w[0] * min_x) / w[1]
    y_max_x = float(- model.b - w[0] * max_x) / w[1]
    plt.plot([min_x, max_x], [y_min_x, y_max_x], '-g')

    # 画出分类线
    plt.show()
"""

if __name__ == '__main__':
    X = []
    y = []
    C = 1.0
    maxIter = 500
    Toler = 0.001

    """
    # 测试数据
    files = open("./data.txt", "r")
    for line in files.readlines():
        val = line.strip().split()
        X.append([float(val[0]), float(val[1])])
        y.append(float(val[2]))
    X = mat(X)
    y = mat(y).T
    """

    # 测试数据：eris
    data = datasets.load_iris()
    X = data['data']
    y = data['target']
    X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size=0.3, random_state=42)

    # 训练模型
    svm = SVM(C, Toler, maxIter, kernelType=("rbf", 3))
    svm.train(mat(X_train), mat(y_train).T)

    # for i in svm.alpha:
    #     if (i > 0):
    #         print(i)

    # 测试数据
    # print("预测值：\n", svm.predict(X))
    score = svm.score(mat(X_train), mat(y_train).T)
    print(score)
    # 数据展示
    # draw(svm)

    """
    # sklearn.svm效果：准确率100%
    # 默认参数
    # SVC(C=1.0, kernel=’rbf’, degree = 3, gamma =’auto_deprecated’, coef0 = 0.0, shrinking = True,
    # probability = False, tol = 0.001, cache_size = 200, class_weight = None, verbose = False,
    # max_iter = -1, decision_function_shape =’ovr’, random_state = None)
    clf = SVC()
    clf.fit(X_train, y_train)
    score = clf.score(X_test, y_test)
    print(score)
    """

输出结果：

3    # 训练次数
0.7047619047619048    # 分类准确度

参考：
《统计学习方法》 李航
SVM SMO Python
支持向量机（SVM）实现
核函数
关于拉格朗日乘子法和KKT条件：
https://blog.csdn.net/xianlingmao/article/details/7919597
https://blog.csdn.net/DawnRanger/article/details/53133450