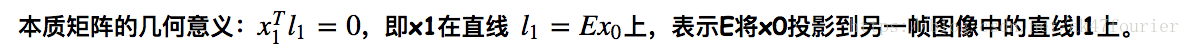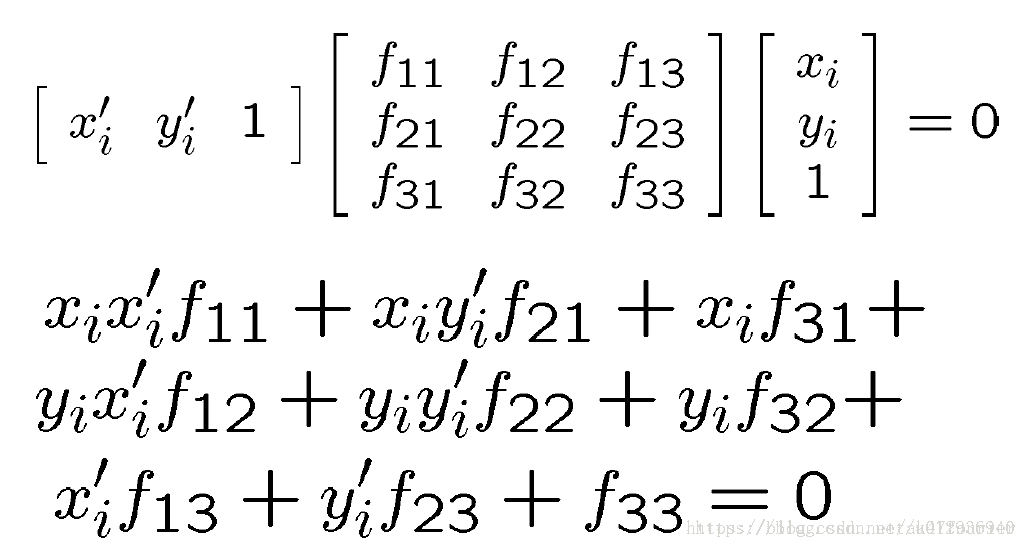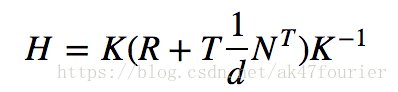/*转载文章,原文链接:
https://blog.csdn.net/u012936940/article/details/80723609
*/
对极几何(Epipolar Geometry)
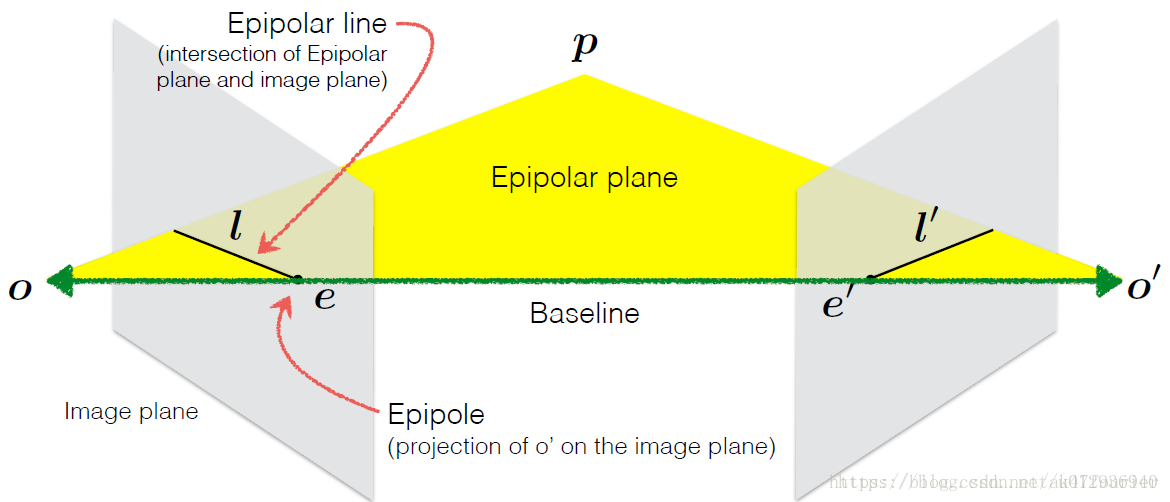
e、e’: 极点,其中e为O’在左图像平面上的像,e’同理
l、l’: 极线
极平面:o、o’、P形成的平面
对极几何描述上述三个量之间的对应关系。
——————————
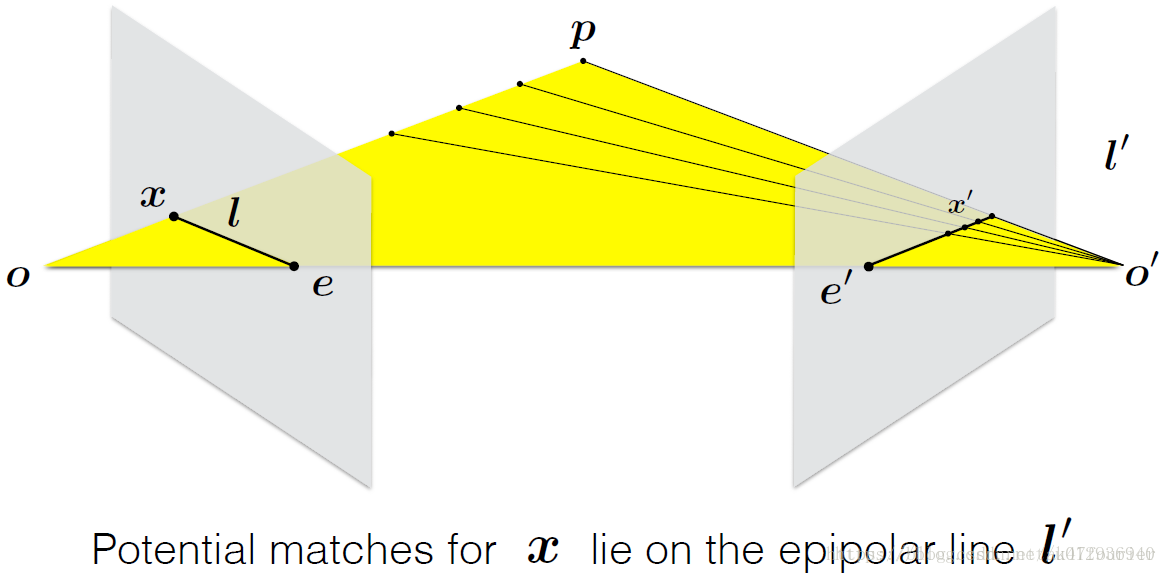
从左图角度看,如果不知道p点的深度信息,射线op是这个点可能出现的空间位置,因为该射线上的点都会投影到同一个像素点,那么在不知道p点的具体位置的情况下,从在右图的位置看时,极线 l’ 就是点p可能出现的位置,即在这条线上的某个地方。
——————————
相机成像平面从左边变到右边,只要旋转+平移就能实现。
即 x’=R(x-t)
如果下图中的三个向量是x,t,x’,那么,这三个向量的混合积为0,即:
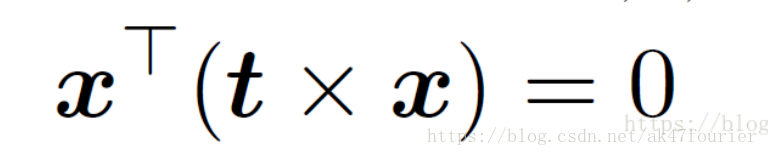
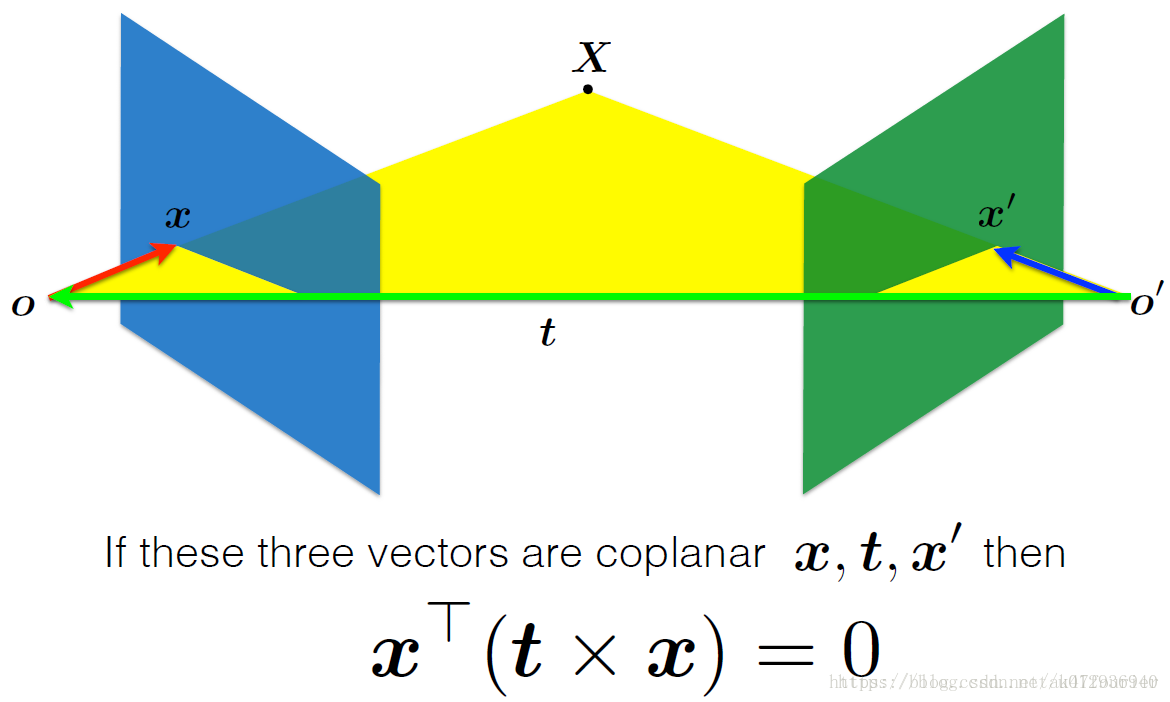
——————————
公式推导过程:
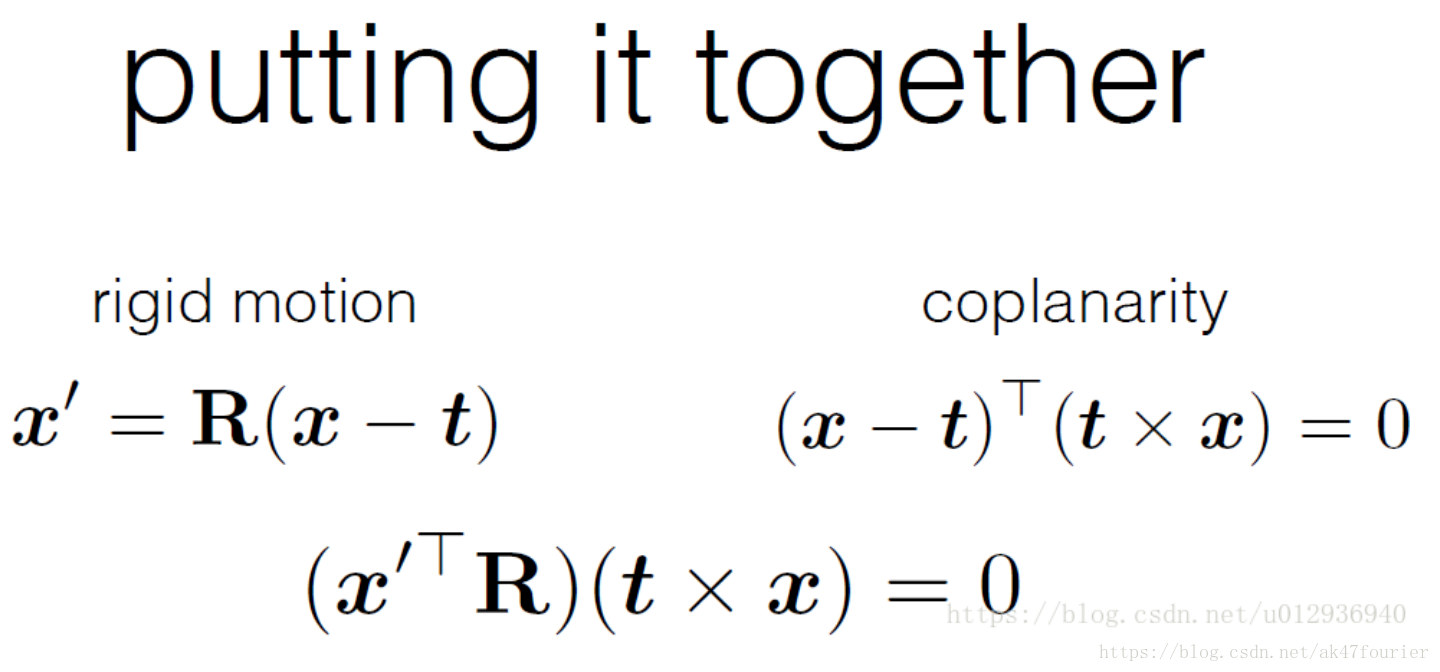
向量叉积计算为:

所以:

上式即为对极约束,描述了不同位置拍摄同一个点时,这两个点构成的约束。
E:本质矩阵(essential matrix),等于t和R的叉积。对E进行分解即可得到两幅图像的位姿关系,当然前提是左右图像中的两个点要正确匹配!!!
注意:这里的左右两个点 x 和 x’ 分别为在相机坐标系下的归一化平面上的点,即 x = [x,y,1],而不是像素平面上的点,因此需首先获得空间点在相机系中的坐标值,之后将其归一化到 z = 1的平面上,才能使用对极约束求解。
————————
注意!!!
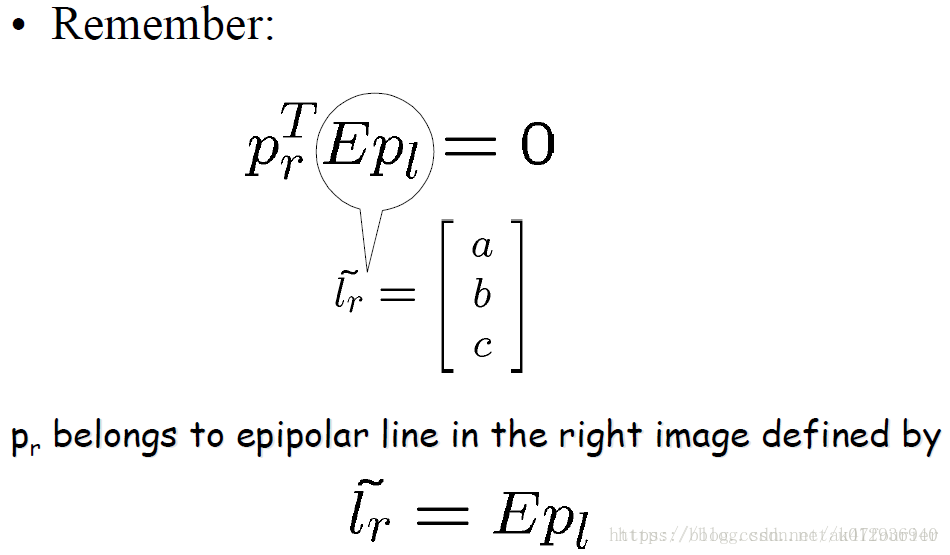
前面说过对极约束中的点是相机系中归一化平面上的点,是三维的点,因此将其和本质矩阵相乘,将得到一个3行1列的向量,而由图可知左图中的点乘以这个向量结果为零,因此可以说点在这个向量构成的直线方程上,同样的
因此,本质矩阵和左像点坐标相乘后得到了一条直线,而该点在右图中的位置就处在这条直线上。本质矩阵和右像点相乘后也得到一条直线,该点在左图中的位置也处在这条直线上。
可以看到:本质矩阵将一个点映射到了一条线上,该点在另一幅图像中可能的位置就在这条线上。
即:
1.本质矩阵的求解
对极约束是一个等式为零的约束,因此对他乘以非零常数后依然成立,这称为本质矩阵的尺度等价性。另一方面,由于平移和旋转各有三个自由度,故 E 共有六个自由度,但由于尺度等价性,因此实际上 E 具有5个自由度。
即最少可用5对点来求解 E,但是这种解法比较麻烦。考虑 E 的尺度等价性,可以使用8对点来求解,即经典的八点法,八点法利用了 E 的线性性质,因此可以通过线性代数求解。
2.基础矩阵的求解
必须注意本质矩阵描述的是几何意义上的约束,他只是将左右相机内的物理坐标进行了约束。实际处理图像时,最直接得到的是某个点在图像中的像素坐标值,由于像素坐标和归一化坐标通过相机内参矩阵进行联系,因此可得


上图中 F 矩阵即为基础矩阵,他不光包含了旋转和平移的信息,还包含了相机的内参信息,使用的是像素坐标。
3.单应矩阵
单应是射影几何中的概念,又称为射影变换。他把一个射影平面上的点映射到另一个平面对应的位置,并且把直线映射为直线,具有保线性质。与对极几何不同的是,对极几何将点映射到线上,而单应矩阵是点对点的关系。要注意的是单应矩阵的适用场景为:当场景中的特征点都落在同一平面上,比如墙、地面等,此时可用单应性估计运动。其描述方程为:
x1=Hx2
其中矩阵 H 为一个3x3的非奇异矩阵,且对矩阵 H 乘以非零的常量依然成立
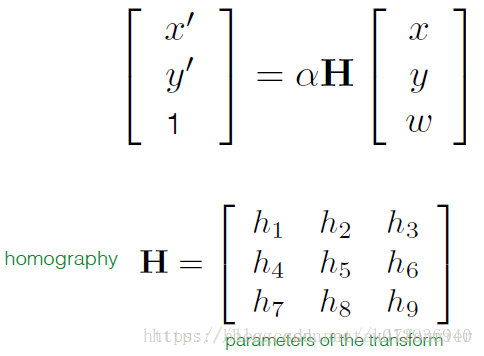
假设已经获得了两幅图像之间的单应矩阵,可得:
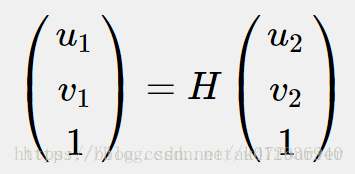
其中左边为图像1中的点,右边为图像2中的点。其具有很多应用,除了估计运动,还能对图像进行校正,比如斜着拍摄一栋楼,通过单应矩阵,可以生成一张看起来是正对着楼拍摄的照片。
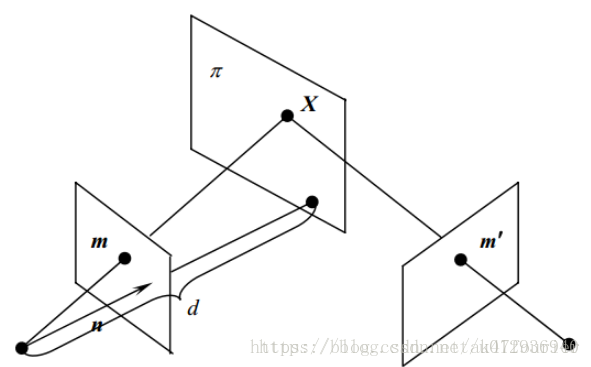
上图表示场景中的平面π在两相机的成像,设平面π在第一个相机坐标系下的单位法向量为N,其到第一个相机中心(坐标原点)的距离为d,则平面π可表示为:
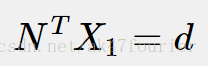
(???why?)
即:
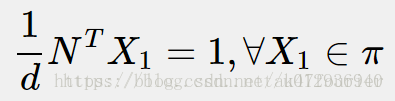
x1、x2分别为点在两个相机坐标系下的坐标,根据前面的推导有:
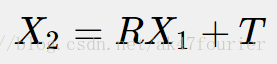
将上面两式子结合可得
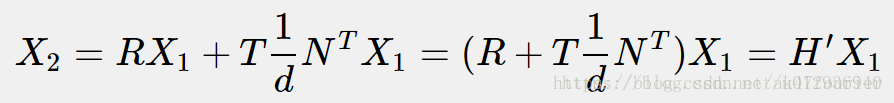
所以同一平面在两个相机坐标系下的单应性矩阵为:
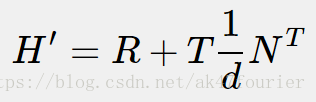
还需要转换到同一平面在两个图像坐标系下的单应性矩阵为,设x1,x2为P在两图像的像点坐标,
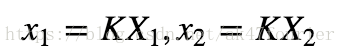
其中K为相机的内参数,代入上面求得单应变换公式:
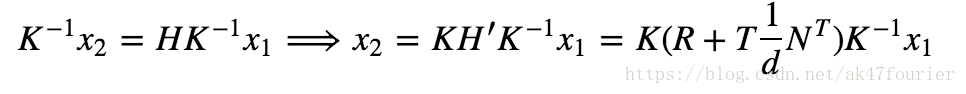
所以,同一平面得到的两个图像间的单应矩阵H为:
4.单应矩阵的求解

写成矩阵形式就是:

注解:如果给定一个单应H={h_ij},给它的元素乘上同一个数a,得到的的单应a*H和H作用相同,因为新单应无非把齐次点x1变成了齐次点a*x1,都是一回事。因此我们可以把a换成1/h22,那么H就变成了只有8个自由元素的矩阵。

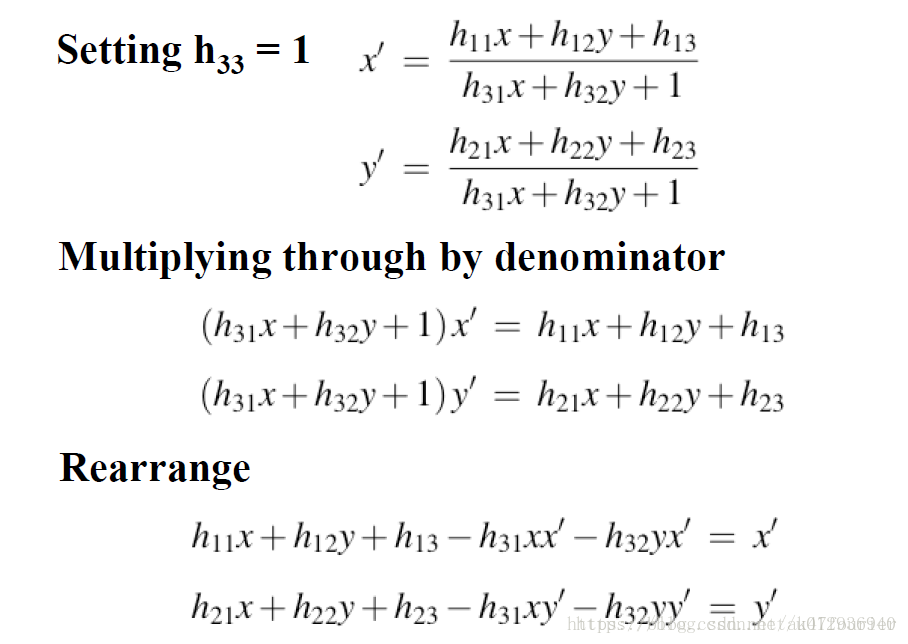

注意:以上做法只有当 h33 即最后一个元素不为零是才能得到正确的解!
以上可以看出,一对匹配点可以得到两项约束,于是自由度为8的单应矩阵可以通过4对匹配点进行求解。
总结
对极约束和单应性:
两幅图像之间的对极约束和场景的结构无关,即对于任意场景结构的图像都是成立的,他不能给出两幅图像上的点的一一对应关系,只能将点映射到线。而单应矩阵可以将点对应到点。
单应矩阵,不像对极约束那样完全不限制场景的结构,单应矩阵要求场景中的点都在同一平面上。
当相机只有旋转没有平移时,可使用单应矩阵估计运动,因为此时平移为0,计算得到的本质矩阵也为0,进而旋转也为0,得到了错误的解,而使用单应性依然能够正确计算。