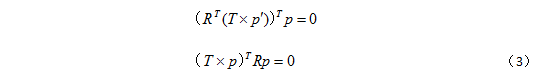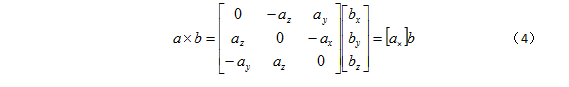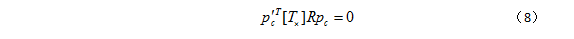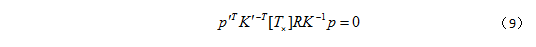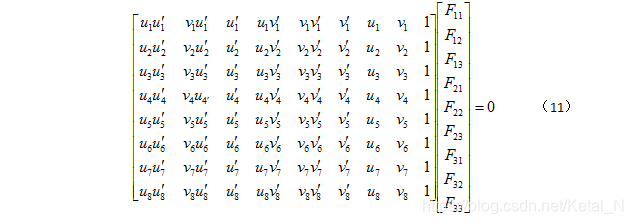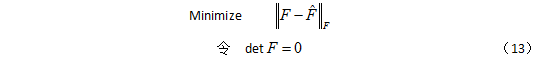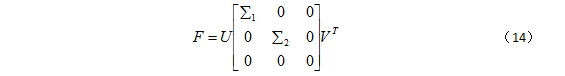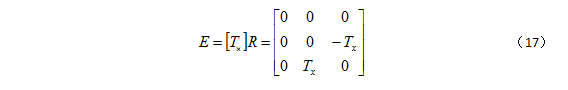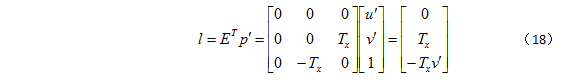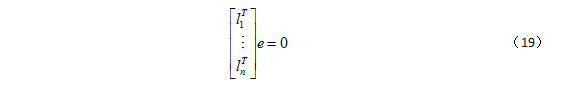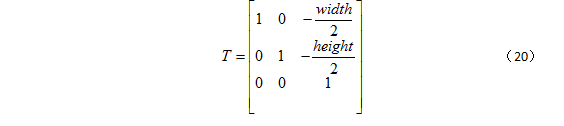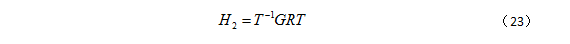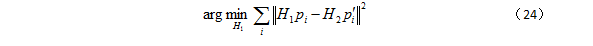【译】对极几何

#本文译自斯坦福大学CS231A计算机视觉课程的课堂笔记，包含自己的理解，如有错误，欢迎指出。原文见：http://web.stanford.edu/class/cs231a/course_notes.html
 

1 介绍

 　通过前面的课程，我们已经知道如何利用典型的相机标定流程（单视角或多视角）来计算相机的内外参数。标定过程以获取到3D世界中的信息而结束。但总的来说，通过单幅图像获取整个3D世界的构造信息是不太可能的。这是因为由3D到2D的映射存在固有的模糊性：一些信息因此而丢失（主要是深度信息）。

　　如图一，我们一开始可能会认为这名男子正拖着比萨尔斜塔。通过仔细的观察，我们知道这只是错觉，这种错觉是因为把不同的深度投影至图像平面引起的。但是，如果我们从一个完全不同的视角观察这一场景，就不会产生这种错觉，并能够立马知道正确的场景布局。
　　本次笔记的重点是：对极几何在多相机观察中的应用。
　　 

2 对极几何

 　在对极几何中，多相机、一个3D点和该点在每个相机图像平面上的投影之间存在有趣的关系。这种与相机、3D点及对应的观察相关的几何被称为该立体图像对的对极几何（epipolar geometry）。

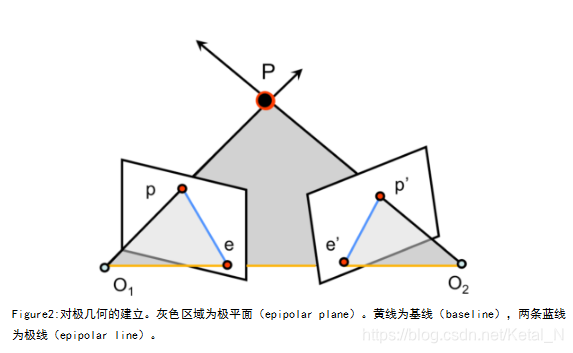
　　如图2所示，标准对极几何的建立需要2个相机观察同一个3D点 P，点 P 在相机图像平面上的投影点分别为 p 和 p’。相机光心为 O₁、O₂ 两点之间的连线成为基线（baseline）。两相机光心与点P构成的平面为极平面（epipolar geometry）。基线与两图像平面的交点称为极点（epipole）e、e’。极平面与两图像平面的交线称为极线（epipolar line）。极线与基线相交于极点。
　　

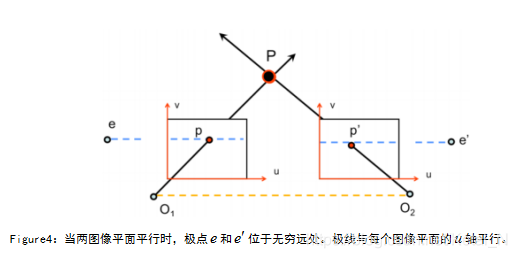
　　图4为对极几何中的一种，当两个图像平面互相平行时出现这种情况。当图像平面互相平行时，由 O₁ 、O₂ 构成的基线平行于图像平面，故极点 e 和 e’ 位于无穷远处。这种情况非常有用，在下面的图像校正小节中会详细介绍。
　　然而在现实世界中，我们不知道3D坐标点 P 的精确位置，但能够确定它在其中一幅图像平面的投影 p 。我们还应该能够知道相机的位置、方向和相机矩阵。利用相机位置 O₁ 、O₂ 和图像点 p，可以确定极平面，然后利用极平面来确定极线。根据定义，点 P 在右图像平面的投影点 p’ 必位于右图像平面的极线上。因此，无需知道场景的3D构造，有了对极线几何的基本理解，我们就可以在图像对之间建立强约束。
　　
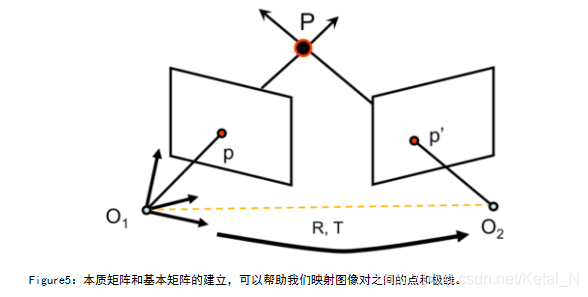
　　我们尝试寻找完美的方法，用于映射图像对之间的点和极线。如果我们采用图5所示的这种原始的极线几何，则还需定义矩阵 M 和 M’（这里的 M 和 M’ 为将3D点映射到它们各自2D图像平面的相机矩阵，其中相机矩阵由两部分构成，左侧部分为相机内参矩阵，右侧部分为相机外参矩阵）。假设世界坐标系与第一个相机坐标系（左侧相机）重合，第二个相机（右侧相机）相对第一个相机旋转 R 并平移 T，则相机投影矩阵如下：

 

3 本质矩阵（the essential matrix）

 　最简单的情况，假设使用的是canonical cameras（不太清除是什么相机，字面翻译觉得不太对，使用这种相机模型是为了把相机内参、外参矩阵去掉），则 K = K’ = I (I为单位矩阵)，等式（1）变为：

　　点 p’ 在左侧相机坐标系下可以表示为：R^Tp’ - R^TT。向量 R^Tp’ - R^TT 和 R^TT 在极平面上，将两向量叉乘：R^TT * (R^Tp’ - R^TT) = R^TT * R^Tp’ = R^T ( T * p’)，得到极平面的法向量。这也表明，在极平面上的点 p（视为向量）垂直于 R^T ( T * p’)，则有点积为零：
　　
　　根据线性代数知识，为叉乘引入一种更为紧凑的表达形式：将两向量 a 、b 之间的叉乘换成矩阵—向量乘积形式：
　　
　　用等式（4）的表达形式改写等式（3），可以将叉乘转换为点乘（数乘）：

　　矩阵 E=|T_X|R 即为本质矩阵（Essential Matrix），对极约束的一种紧凑形式为：

　　本质矩阵 E 为3x3大小的矩阵，包含5个自由度（分别为右侧相机绕左侧相机 X,Y,Z 轴的旋转和沿左侧相机原点的平移矢量）。矩阵的秩为2，为奇异矩阵（不可逆）。
　　本质矩阵用于计算与点 p 和点 p’ 对应的极线。例如，l’=Ep 给出了右侧相机图像平面中的极线。同样，l=Ep’ 给出了左侧相机图像平面中的极线。本质矩阵 E 的属性有：与极点的点积为零，即 Ee=E^Te’ =0 。因为左侧相机图像平面中的任意点 x（不包括点e），其在右侧相机中对应的极线为 l’=Ex，极点 e’ 在极线上。因此对任意点 x，极点 e’ 满足e’^T(Ex)=(e’^TE)x=0，故 e’^TE=0 。同理，Ee=0。
 

4 基础矩阵

 　虽然我们得到了canonical camera下的 p 和 p’ 之间的关系，但我们应该找到相机不是canonical条件下更普适的表达式。我们得到的真实的投影矩阵是：

　　首先，定义 p_c=K^-1p，p’_c=K’^-1p’，p_c 和 p’_c 为canonical相机模型下点 P 在相机图像下的投影。在canonical条件下，有：

　　将 p_c 和 p’_c 的值带入上式，有：

　　矩阵 F=K’^-T[T_*]RK^-1 即为基本矩阵（Fundamental Matrix），其作用和本质矩阵相似，但是基本矩阵中包含了相机矩阵 K、K’ 及两相机之间的相对位置关系。因此，基础矩阵 F 也可用来计算与 p 和 p’ 相对应的极线，即使是在相机矩阵 K、K’ 和相机之间相对平移 T、相对旋转 R 未知的情况下。同本质矩阵相似，我们可以通过基本矩阵和图像平面上的投影点计算对应的极线 l’=Fp 和 l=F^Tp’ 。基本矩阵和本质矩阵之间的主要区别是：基本矩阵由7个自由度，本质矩阵有5个自由度。
　　但基础矩阵到底有多么有用呢？同本质矩阵一样，如果知道了基本矩阵，然后利用一幅图像中的已知点给出其在另一幅图像中的对应点的约束条件。因此，无需知道点 P 在3D空间中的实际位置，也无需知道相机的内外参数，就可以建立任何点 p 和点 p’ 之间的关系。

4.1八点算法

 　可以使用由相机参数矩阵乘积定义的基础矩阵这一假设似乎太大了。但是，通过给定同一场景的两幅图像，且在相机内外参数未知的情况下，是可以估算出基础矩阵的。这种求解的方法被称为8点算法（the Eight-Point Algorithm）。1981年，Longuet-Higgins提出了八点算法；1995年，Hartley 对其进行了拓展。8点算法假定两图像上至少有8对对应点可以获取。
　　每对对应点 p_i=(u_i,v_i,1) 和 p’_i=(u’_i,v’_i,1) 给出极线约束：p’_i^TFp_i=0。将极线约束以下列的形式给出：

　　该方程为标量方程，一个方程约束一个自由度，故需要8个约束求解基本矩阵：

　　上式可以写成：

　　上式中，W 是由N≥8 对对应点组成的 N*9 矩阵，f 为待求取的基础矩阵。
　　实际应用中，常用大于8对的对应点构造一个更大的矩阵，可以减少噪声测量造成的影响。该齐次方程的解可通过SVD（Singular Value Decomposition 奇异值分解法）法求解最小二乘解获取。SVD法可得到基础矩阵的近似解 $\hat{F}$ ，该矩阵可能满秩。但我们知道基础矩阵的秩为2。因此，我们寻找秩为2且近似于 $\hat{F}$的解。因此求解下列最优解问题：
　

　　仍采用SVD法求解，将 $\hat{F}$进行奇异值分解： $\hat{F}＝Ｕ\sum$V^T，则秩为2的最优解为：

4.2 归一化八点算法

 　实际上，上述方法求得的解并不精确。通常，点 p_i 与其对应的极线 l_i=F^Tp’ 间的距离很大，通常在10+个像素级别上。为了减小误差，利用改进的8点算法，即归一化的8点算法。
　　标准的8点算法的主要问题源于矩阵W对于奇异值分解是病态的。为了使SVD可以求解出解，W应该有一个等于（或接近）零的奇异值，其他的奇异值不为零。然而，由于相机像素范围很大，两幅图像上对应点 p_i 的坐标值经常也会很大（如 p_i=(1832,1023,1)）。如果用于构造矩阵W的图像点位于图像的一个相对小的区域范围，那么每对向量 p_i 和 p’_i 则比较接近。因此，所构造的矩阵W会有一个较大的奇异值，且其余的奇异值相对较小。
　　为解决这一问题，在构造矩阵W前，将图像点进行归一化。即对图像坐标系进行平移和缩放来实现对W矩阵的预先调节。第一步：新系的原点位于图像点的质心（平移）；第二步：变换后图像上的点距原点的平均距离为 $\sqrt{2}$ 个像素（缩放）。可以用矩阵 T ,T’ 来表示上述的变换。
　　然后就可以将坐标进行归一化：

　　利用8点算法计算归一坐标系下的矩阵 F_q 。矩阵 F_q 为归一化坐标系下的基础矩阵。为了可以在正常坐标系下使用，对矩阵 F_q 去归一化：

　　最后，求得的矩阵 F 在实际测试下有很好的效果。
　　 

5 图像校正（Image Rectification）

 　回顾一下，两幅图像彼此平行情况下的对极几何。首先计算本质矩阵 E。假设两相机具有相同的相机矩阵 K 且两相机之间没有相对旋转（R=I）。这种情况下，只有一个沿轴 x 的平移：T=(T_x,0,0)。则有：

  一旦本质矩阵 E 已知，则图像平面中与点对应的极线的方向便已知。与点 p’ 相对应的极线 l 的方向：

 可以看到，l 处于水平方向，l’ 也是处于水平方向。

  利用对极约束 p’^TEp=0，可以得到结论：v=v’，即 p 和 p’ 在垂直方向上（v 坐标）具有相同的坐标。这就使得对应点之间存在十分明显的关系。因此，在辨别图像对上对应点之间的关系时，校正或者使图像对相互平行的操作就很有用。

  图像对的校正无需两相机的相机矩阵 K,K’，也不需要相机间的相对位置关系。可以利用归一化8点算法得到的基础矩阵。有了基础矩阵，即可计算每个图像点 p 和 p’ 对应的极线 l 和 l’。
通过极线，可以得到每幅图像的极点 e 和 e’ （因为极点是所有极线的交点）。在实际测量中，由于噪声的存在，所有的极线可能不会都相交于一点。可以通过拟合点到所有极线的最小平方差计算极点。每条极线都可用一个向量表示，因此该极线上的所有点都满足：{x|l^Tx=0}。将极线定义为：l_i={l_i1,l_i2,l_i3}^T，则可得到一个线性方程，并用SVD法求解极点 e：

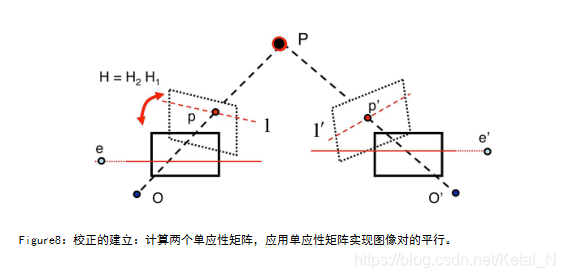
  求得的极点 e 和 e’ 不是在水平轴的无穷远处。如果求得的极点是在水平轴的无穷远处，则由定义可知，图像对已经平行。因此，需要深入探究，怎样可以使得图像对平行：能够找到一个单应性矩阵将极点映射到水平轴的无穷远处吗？具体一点就是，我们想找到一对单应性矩阵H,H’，利用它们将极点 e’ 映射到无穷远。我们开始寻找可以将极点映射到水平轴无限远 (f,0,0) 处的单应性矩阵H₂。对该单应性矩阵的选择条件有很多，我们应该选取合理的条件。一种条件为：单应性矩阵的作用和对图像中心的附近点做平移、旋转的变换相似。
  获得该变换的第一步为：平移第二幅图像，使其中心点在齐次坐标系下的坐标 (0,0,1) 为。利用下面的平移矩阵：

  第二步：利用旋转矩阵将极点放置在水平轴上坐标为 (f,0,1) 处。如果平移后的极点 Te’ 在齐次坐标系下的坐标为 (e’₁,e’₂,1)，然后旋转矩阵为：

  当 e’≥0 时，α=1，否则 α=-1。对 (f,0,1) 处给定的任一点应用该矩阵后，只需要使用上述矩阵G即可将给定点变换至水平轴无穷远处的 (f,0,0)：

  利用完G矩阵后，最终得到位于无穷远处的极点。因此，用于校正第二幅图像的单应性矩阵为 H₂：

  矩阵 H₂ 找到后，开始寻找第一幅图像对应的单应性矩阵 H₁。我们求图像对应点之间的距离平方和的最小值求解 H₁:

  可以证明矩阵 H₁ 的形式如下：

上式中，F=[e]_*M，且：

向量 a(a₁,a₂,a₃) 稍后计算。
  首先要弄清楚矩阵M 是什么。33 大小的斜对称矩阵 A 具有如下性质：A=A³。因为任何的叉乘矩阵 [e]_* 都是斜对称矩阵，因此基础矩阵也具有上述性质：

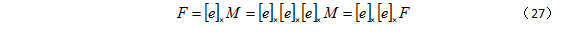
由上式可得：

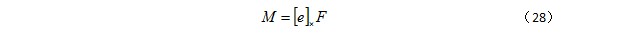
  如果矩阵 M 的列数以 e 的任意倍数增加，基础矩阵 F= [e]_*M 仍具有上述的性质。因此，矩阵 M 的一般形式为：

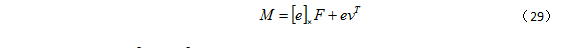
实际计算时，取 v^T=[1,1,1] 计算效果更好。
  为了最终求解出 H₁，需计算出 H_A 的一个值。回顾一下，我们解 H₁,H₂ 是为了求等式（24）的最小值问题。现在已求得 H₂，M ，进行如下替换： $\hat{p}$_i=H₂Mp*、 $\hat{p}$‘_i=H₂Mp’，最小值问题则变为：

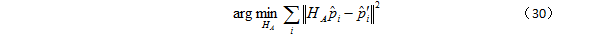
  实际上，如果 $\hat{p}$_i=( $\hat{x}$_i, $\hat{y}$_i,1)， $\hat{p}$'_i=( $\hat{x}$'_i, $\hat{y}$'_i,1)，最小值问题可替换为：

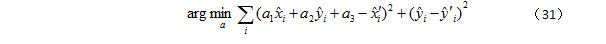
又因 $\hat{y}$_i- $\hat{y}$'_i 为常量，最小值问题可进一步简化为：

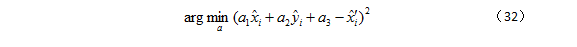
  最终，分解为解最小二乘问题 Wa=b，其中：

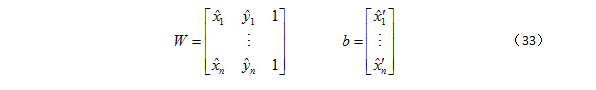
  计算出 a，然后计算 H_A ,最后计算出 H₁ 。至此，得到了用于图像对校正的单应性矩阵 H₁, H₂。
 
 

文中公式较多，如有错误请见谅。转载请注明出处，谢谢！