对极约束

设第一帧到第二帧的运动为$R,t$,相机中心为$O_1,O_2$,$I_1$中特征点$p_1$对应$I_2$中的特征点$p_2$,如果匹配正确,说明是同一个空间点在两个成像平面的投影。连线$\overrightarrow{O_{1}p_1}$和连线$\overrightarrow{O_{2}p_2}$相交于点$P$。$O_1,O_2,P$确定一个平面,为极平面。$e_1,e_2$为极点,$O_1O_2$为基线,$l_1,l_2$为极线。
仅从第一帧的角度看,射线$\overrightarrow{O_{1}p_1}$是某像素可能出现的空间位置,该射线上所有点都会投影到该像素点,连线$\overrightarrow{e_2p_2}$是$P$点在第二帧中可能出现的投影位置,即射线$\overrightarrow{O_{1}p_1}$在第二帧中的投影。而$p_2$确定,所以能推断出$P$的位置。
数学表达
在第一帧坐标系下,$P$点坐标为$\right[X,Y,Z\left]^T$,注意这不是世界坐标系下的坐标。
参考《视觉SLAM十四讲》P86
$ZP_{uv} = Z\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K\left( RP_w + t \right) = KTP_w$,$P_w$为世界坐标系下三维坐标点。
上式两侧都是其次坐标,因为齐次坐标乘上非零常数后表达同样的意思,所以可以把$Z$去掉。
$P_{uv} = KTP_w$($TP_w$表示一个世界坐标系下的齐次坐标变换为相机坐标系下,为了使它与$K$相乘,需要取它前三维组成向量,$TP_{w}$最后一维为1)
齐次坐标:https://blog.csdn.net/jeffasd/article/details/77944822
知道两个不同帧中的像素点$p_1,p_2$的像素坐标。
$s_1p_1 = KP,s_2p_2 = K \left( RP + t \right)$
$x_1 = s_1K^{-1}p_1 = P, x_2 = s_2K^{-1}p_2 = RP + t$
所以有$Rx_1 + t = x_2$
同时左乘$t^{\wedge}$,得$t^{\wedge}x_2 = t^{\wedge}Rx_1$,同时左乘$x_2^T$,$x_2^Tt^{\wedge}x_2 = x_2^Tt^{\wedge}Rx_1$
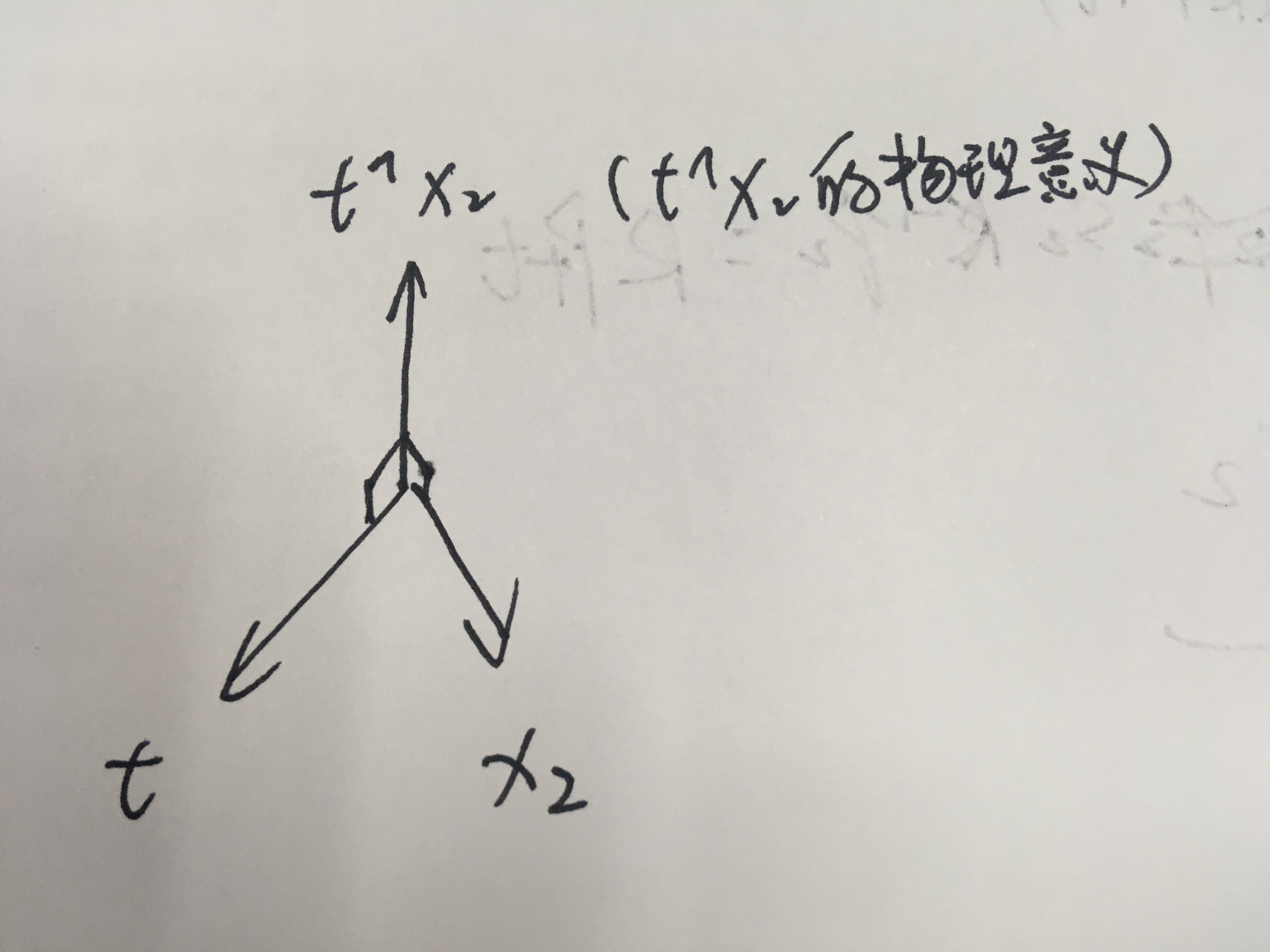
$t^{\wedge}x_2$是一个与$t$和$x_2$都垂直的向量。将它和$x_2$作内积,将得0。
得一个简洁的式子:$x_2^{T}t^{\wedge}Rx_1 = 0$
重新代入$x_1,x_2$有$\left( s_2K^{-1}p_2\right)^{T}t^{\wedge}R\left( s_1K^{-1}p_1\right) = 0 $,$s_1,s_2$为标量。($\left( \lambda A \right)^T = \lambda A^{T},\lambda\in P$ )
所以有:$p_2^TK^{-T}t^{\wedge}RK^{-1}p_1 = 0$,即对极约束,中间包含了平移和旋转,将其中分成两个矩阵基础矩阵F和本质矩阵E。
简化为:
$E = t^{\wedge}R,F = K^{-T}EK^{-1},x_2^TEx_1 = p_2^TFp_1 = 0$
相机位置关系求解有以下两步:
1.根据配对点位置求E和F。
2.根据E和F求R,t。
其中F的相机内参已知。
本质矩阵性质:
1.E在不同尺度下是等价的
2.本质矩阵E的奇异值是$\left[\sigma,\sigma,0\right]^T$的形式。
3.平移与旋转各有3个自由度,所以$t^{\wedge}R$有6个自由度,由于尺度等价性,E只有5自由度
最少用5对点求解E。但是E的性质是非线性的,难求解,只考虑它的尺度等价性,用八对点估计E(八点法),利用了E的线性性质。
考虑一对匹配点,x 1 =[ u 1 , v 1 , 1] T , x 2 =[ u 2 , v 2 , 1] T


由八对特征点,可求本质矩阵E中的各个元素。