多项式回归算法(Polynomial Regression)属于有监督的回归(Regression)学习算法。回归(Regression)算法通过建立变量之间的回归模型,通过学习(训练)过程得到变量与因变量之间的相关关系。回归(Regression)分析可以用于预测模型或分类模型。常见的回归算法包括:线性回归(Linear Regression)、非线性回归(Non-linear Regression)、逻辑回归(Logistic Regression)、多项式回归(Polynomial Regression)、岭回归(Ridge Regression)、套索回归(Lasso Regression)和弹性网络回归(ElasticNet Regression)。其中线性回归、非线性回归和逻辑回归最为常用。
很多场合线性模型无法很好的拟合目标数据曲线,这就需要引入非线性回归模型。对于非线性回归存在多种策略,第一种策略是将非线性回归转化成线性回归;第二种策略是将非线性回归转化成多项式回归。多项式回归中,加入了特征的更高次方(例如平方项或立方项),也相当于增加了模型的自由度,用来捕获数据中非线性的变化。
1 算法原理
多项式回归的主要思想就是通过历史数据拟合出多项式回归的方程,并利用多项式回归的方程对新的数据进行预测。多项式回归的方程如下:
从上式可以得出:要想获得一个与目标数据集完美拟合的多项式回归模型,实质就是求解出每个特征自变量的权值θ。线性回归首先构建一个凸函数的优化函数(诸如: 给定的函数值与模型预测值之差的平方和最小),并使用最小二乘法和梯度下降法来计算最终的拟合参数。
逻辑回归(Logistic Regression)分类算法的核心步骤如下:
- 构造 predict 函数, 采用多项式回归的方程;
- 构造 loss 函数, 给定的函数值与模型预测值之差的平方和最小;
- 使用最小二乘法和梯度下降法计算最终的拟合参数;
- 反复迭代优化最终的拟合参数;
- 输出最终的拟合参数
逻辑回归(Logistic Regression)分类算法的核心优势如下:
- 计算伸缩性: 计算复杂度可控;
- 参数依赖性: 可调节参数较少;
- 普适性能力: 适用于连续型和离散型数据集, 关注过拟合问题;
- 抗噪音能力: 对缺失数据和异常数据比较敏感, 需要特别关注;
- 结果解释性: 理论简练, 解释性好。
2 算法实例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
sample_cnt= 32
data_x = np.linspace(start = 0, stop = sample_cnt/4, num = sample_cnt).reshape(-1, 1)
rand_n = np.random.randn(sample_cnt).reshape(-1, 1)
# curve using linear
curve_linear = np.sin(data_x)
θ0, θ1 = 0.3, -0.05
curve_linear = yr = θ0 + θ1*data_x
curve_linear += rand_n * 0.03
# curve using polynomial
θ0, θ1, θ2, θ3 = 0.1, -0.02, 0.03, -0.04
curve_polynomial = θ0 + θ1*data_x + θ2*(data_x**2) + θ3*(data_x**3)
curve_polynomial += rand_n
plt.subplot(2, 2, 1)
plt.plot(data_x, curve_linear, 'b.')
plt.xlabel("np.linspace(0, 8, 32)")
plt.ylabel("curve_linear(data_x)")
plt.subplot(2, 2, 2)
plt.plot(data_x, curve_polynomial, 'b.')
plt.xlabel("np.linspace(0, 8, 32)")
plt.ylabel("curve_polynomial(data_x)")
poly_features_1 = PolynomialFeatures(degree = 3)
linear_reg = LinearRegression()
linear_reg.fit(poly_features_1.fit_transform(data_x), curve_linear)
print(poly_features_1.get_params())
fit_x = np.linspace(start = 0, stop = sample_cnt/4, num = 1024).reshape(-1, 1)
fit_linear = linear_reg.predict(poly_features_1.fit_transform(fit_x))
plt.subplot(2, 2, 3)
plt.plot(fit_x, fit_linear, 'r-')
plt.plot(data_x, curve_linear, 'b.')
plt.xlabel("np.linspace(0, 8, 32)")
plt.ylabel("curve fitting using Polynomial")
poly_features_3 = PolynomialFeatures(degree = 3)
linear_reg_best = LinearRegression()
linear_reg_best.fit(poly_features_3.fit_transform(data_x), curve_polynomial)
fit_x = np.linspace(start = 0, stop = sample_cnt/4, num = 1024).reshape(-1, 1)
fit_linear_best = linear_reg_best.predict(poly_features_3.fit_transform(fit_x))
plt.subplot(2, 2, 4)
plt.plot(fit_x, fit_linear_best, 'r-')
plt.plot(data_x, curve_polynomial, 'b.')
plt.xlabel("np.linspace(0, 8, 32)")
plt.ylabel("curve fitting using Polynomial")
hypo = linear_reg.predict(poly_features_1.fit_transform(data_x))
hypo_best = linear_reg_best.predict(poly_features_3.fit_transform(data_x))
print(mean_squared_error(hypo, curve_linear)) # MSE: 0.00055
print(mean_squared_error(hypo_best, curve_polynomial)) # MSE: 0.61483
#Adjust subgraph spacing
plt.subplots_adjust(wspace =0.3, hspace =0.4)
plt.show()
构造线性函数:
,并在线性函数上添加随机值;构造多项式函数
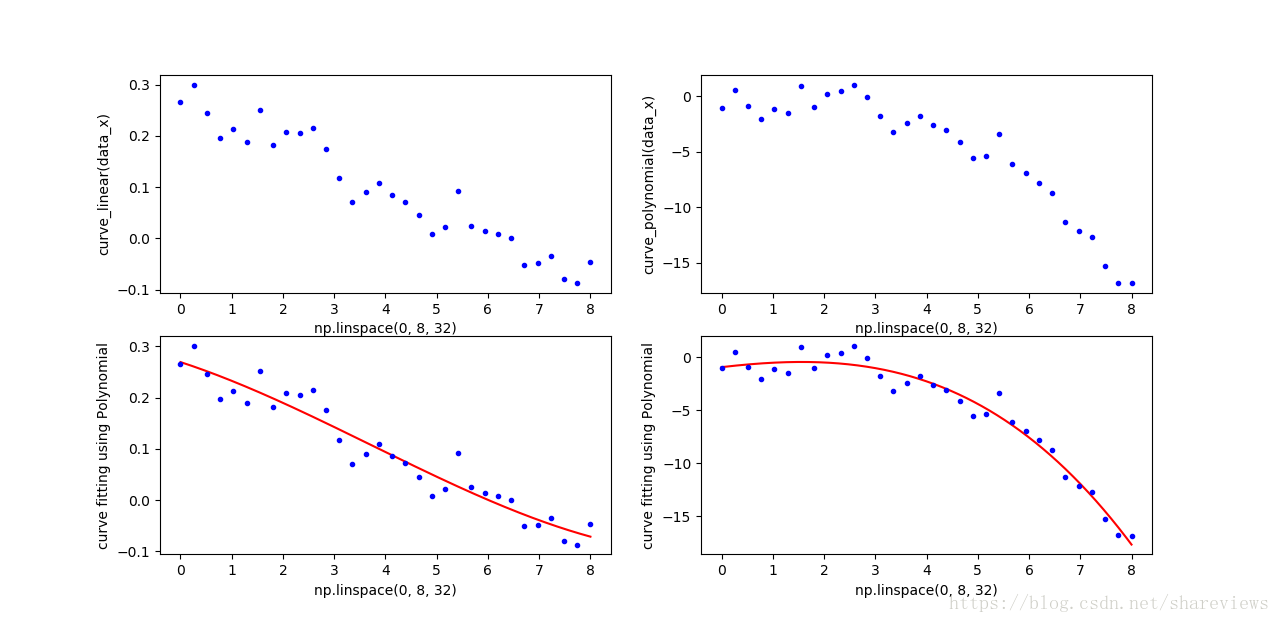
,并在多项式函数上添加随机值;使用SkLearn的LinearRegression模块拟合曲线。效果如下图。
可以使用sklearn.metrics.mean_squared_error 评估误差。从结果可见,多项式函数可以拟合线性函数,但是出现过拟合现象。多项式函数拟合多项式函数最佳,但是也需要多项式的阶数,用高阶多项式函数拟合低阶多项式函数也会出现过拟合现象。
- 对于线性数据集,多项式拟合函数的MSE为0.00055
- 多余多项式数据集,多项式拟合函数的MSE为0.61483
3 典型应用
线性回归在定量和定性的数据中有广泛的用途。例如:图像&视频质量评价研究中,研究人员提出一个新的客观质量图像&视频质量评价指标,在横向对比分析中,研究人员需要将其评价指标其它类型的指标(PNSR, SSIM, CMOS等)做线性回归,以期望度量指标的最终价值。
系列文章
参考资料
- [1] 周志华. 机器学习. 清华大学出版社. 2016.
- [2] [日]杉山将. 图解机器学习. 人民邮电出版社. 2015.
- [3] 佩德罗·多明戈斯. 终极算法-机器学习和人工智能如何重塑世界. 中信出版社. 2018.
- [4] 李航. 统计学习方法. 2012.