牛客国庆集训派对Day4 F 导数卷积（NTT）

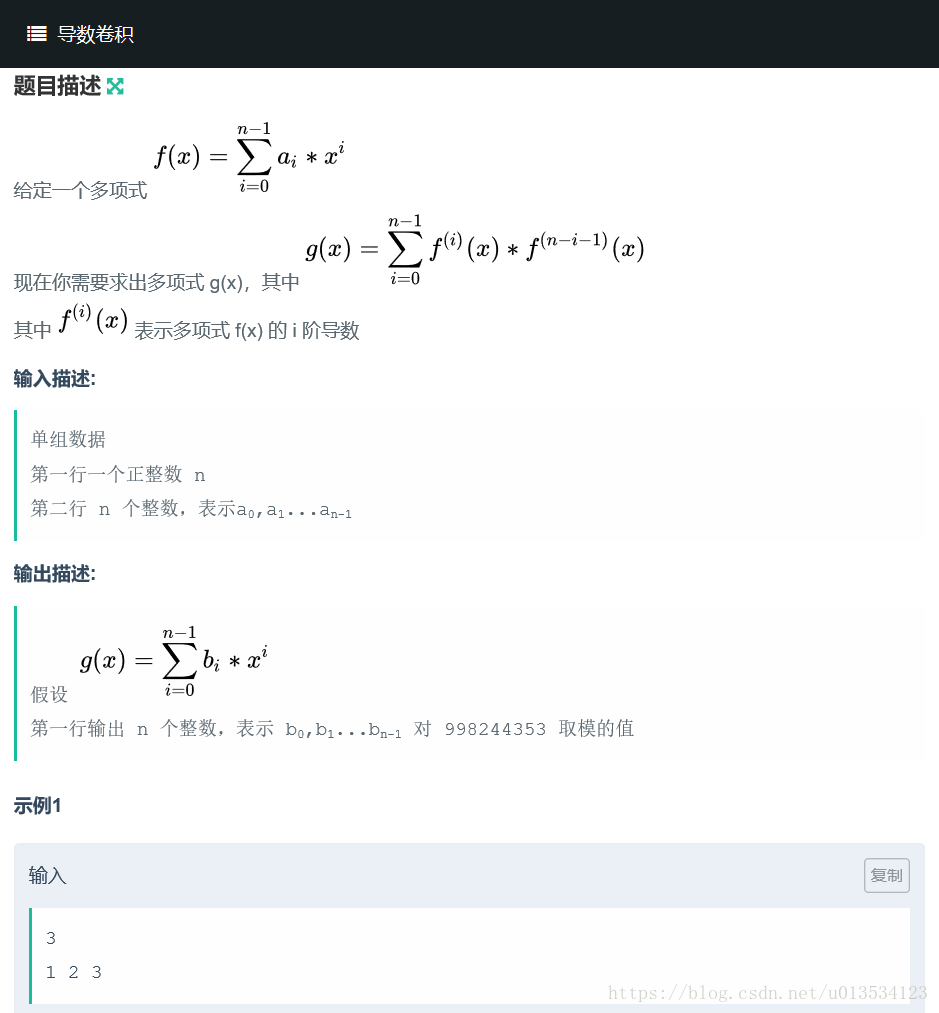
要求计算两个多项式求导的卷积。

我们首先把单个多项式求i阶导的式子写出来：

$\large f^{(i)}=\sum_{j=i}^{n-1}a_{j}*\frac{j!}{(j-i)!}$

那么总的式子就是：

$\large g=\sum_{i=0}^{n-1}(\sum_{j=i}^{n-1}a_{j}*\frac{j!}{(j-i)!}*\sum_{k=n-i-1}^{n-1}a_k*\frac{k!}{(k-n+i+1)!})$

虽然说这个式子如果可以交换求和次序，把i放到内层，然后j和k放到外层循环，这样可以很简单的用两次NTT求出结果，但是注意到这个里面有一个括号，而且j和k的和式是用乘法连接的，所以说这个求和次序并不能交换。如果用暴力的做法，即使用NTT优化掉一个sigma，还剩下两个，依然不能求解。

于是我们考虑换一下多项式求i阶导之后的形式，直接用多项式表示法去表示，即第j位对应x的j次方的系数：

$\large f^{(i)}(x)=\sum_{j=0}^{n-1}a_{i+j}*\frac{(i+j)!}{j!}$

注意到i阶导之后的多项式应该只有n-1-i次，但是这里为了方便直接和式写道n-1，后面的因为 $\large a_{i+j}$ 没有意义，直接看作0，对结果不产生影响。我们不妨设F(i)=ai*(i+j)!。然后本题最后的结果也是一个多项式，我也不妨把这个多项式的每一个幂次对应的系数单独拆出来看，那么x的d次幂对应的系数是：

$\large g_d=\sum_{i=0}^{n-1}\sum_{j=0}^{d}F(i+j)*\frac{1}{j!}*F(n-i-1+d-j)*\frac{1}{(d-j)!}$

即对应系数是每一个i阶导函数和n-i-1阶导函数对应项的卷积。接着，同样的对x的d次方的系数产生影响的阶导不会有这么多，但是我们把不满足条件的导次的贡献用0来表示即可。

然后我们令i=i+j，那么有：

$\large g_d=\sum_{i=0}^{n-1+d}F(i)*F(n-1+d-i)*\sum_{j=0}^{d}\frac{1}{j!}*\frac{1}{(d-j)!}$

这样这个式子左右两边互不影响，就可以拆成左右两个部分，而这两个部分是两个卷积的形式，所以用两个NTT分别计算两个和式的每一项即可。最后再O(N)乘到一起即可，时间复杂度O(NlogN)。具体见代码：

#include<bits/stdc++.h>
#define file(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define IO ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define mod 998244353
#define LL long long
#define N 270010
using namespace std;

int inv[N],fac[N],ifac[N];
int c[N],d[N],a[N],n;

int qpow(int a,int b)
{
    int ans=1;
    while(b)
    {
        if(b&1)ans=(LL)ans*a%mod;
        a=(LL)a*a%mod; b>>=1;
    }
    return ans;
}

namespace NTT
{
    #define g 3
    int x[N],y[N],wn[N];

    void init()
    {
        for(int i=0;i<21;i++)
        {
            int t=1<<i; wn[i]=qpow(g,(mod-1)/t);
        }
    }

    void brc(int *F,int len)
    {
        int j=len/2;
        for(int i=1;i<len-1;i++)
        {
            if(i<j)swap(F[i],F[j]);
            int k=len/2;
            while(j>=k) j-=k,k>>=1;
            if(j<k)j+=k;
        }
    }

    void NTT(int *F,int len,int t)
    {
        int id=0; brc(F,len);
        for(int h=2;h<=len;h<<=1)
        {
            id++;
            for(int j=0;j<len;j+=h)
            {
                int E=1;
                for(int k=j;k<j+h/2;k++)
                {
                    int u=F[k],v=(LL)E*F[k+h/2]%mod;
                    F[k]=(u+v)%mod,F[k+h/2]=((u-v)%mod+mod)%mod;
                    E=(LL)E*wn[id]%mod;
                }
            }
        }
        if(t==-1)
        {
            for(int i=1;i<len/2;i++)swap(F[i],F[len-i]);
            LL inv=qpow(len,mod-2);
            for(int i=0;i<len;i++)F[i]=(LL)F[i]%mod*inv%mod;
        }
    }

    void multiply(int *a,int len1)
    {
        NTT(a,len1,1);
        for(int i=0;i<len1;i++) a[i]=(LL)a[i]*a[i]%mod;
        NTT(a,len1,-1);
    }
}


void init()
{
    fac[0]=ifac[0]=inv[0]=1;
    fac[1]=ifac[1]=inv[1]=1;
    for(int i=2;i<N;i++)
    {
        fac[i]=fac[i-1]*(LL)i%mod;
        inv[i]=(mod-mod/i)*(LL)inv[mod%i]%mod;
        ifac[i]=ifac[i-1]*(LL)inv[i]%mod;
    }
}

int main()
{
    IO; init(); cin>>n;
    for(int i=0;i<=n-1;i++) cin>>a[i];
    int len=1;while(len<n*2+10) len<<=1;
    for(int i=0;i<=n-1;i++)
        c[i]=(LL)a[i]*fac[i]%mod;
    for(int i=0;i<=n-1;i++) d[i]=ifac[i];
    NTT::init();
    NTT::multiply(c,len);
    NTT::multiply(d,len);
    for(int i=0;i<=n-1;i++)
        cout<<(LL)c[i+n-1]*d[i]%mod<<" \n"[i==n-1];
    return 0;
}

牛客国庆集训派对Day4 F 导数卷积（NTT）

猜你喜欢