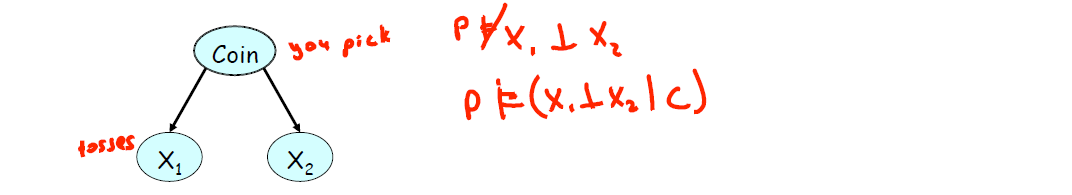概率图模型(02)下: 贝叶斯网两等价观点(条件独立和因子分解)

　　本博客中 PGM 系列笔记以 Stanford 教授 Daphne Koller 的公开课 Probabilistic Graphical Model 为主线，并参阅 Koller著作及其翻译版对笔记加以补充。博文的章节编号与课程视频编号一致。
　　博文持续更新（点击这里见系列笔记目录页），文中提到的资源以及更多见 PGM 资源分享和课程简介。

　　第 02 部分视频分为两篇博文记录（可点击 Part 链接进入）：

　　Part 1：上篇主要讲解了贝叶斯网络（Bayesian Network Fundamentals）相关知识，从链式法则推导出网络的因子分解，讨论了不同推断的形式（Reasoning Patterns），网络中概率影响的流动性（Flow of Probabilistic Influence），介绍了有效迹（Active Trail）的定义，并举例 V 型结构（V-structure）和讲解四种双边迹。　
　　Part 2：本篇将继续贝叶斯网络基础的讲解，主要目的在于诠释包括贝叶斯网络的两种等价观点，即条件独立和因子分解（Independence 和 Factorization）的等价性；解释 d-分离 和 I-map 的概念，并介绍伯努利和多项式这两种朴素贝叶斯分类器。

4. 条件独立性（Conditional Independence）

　　一个贝叶斯网络中，两个变量是否相关（相互影响）不是一概而论的，否则那网络模型也太容易建立和求解了。事实上，变量的独立性有时是和某些中间变量是否被观测到有关联的，即这时变量之间通常有一种条件独立性。下面我们来逐步对此作出解释。

4.1 独立和条件独立

　　首先介绍两种变量关系：独立和条件独立。对于分布 $P$ 中随机变量 $X,Y,Z$

独立（Independence）: 若 $P(X,Y)=P(X)P(Y)$ ，则称 $X,Y$ 独立，记作 $P\models X\perp Y$ .
此时以下三条陈述等价
- $P(X,Y)=P(X)P(Y)$
- $P(X|Y)=P(X)$
- $P(Y|X)=P(Y)$

例如，下图中只考虑 $I,D$ 的分布（分布状态中 $I,D$ 取值相同的概率累加，忽略 $G$ ，即下图中每三行一累加），得到下图中间的表 $P(I,D)$ . 右边两小表分别为 $I,D$ 的边缘分布 $P(I)$ 和 $P(I)$ ，计算易得满足 $P(I,D)=P(I)P(D)$ . 即 $I,D$ 独立，此时 $G$ 未被观测到（“忽略 $G$ ”就是这个意思）。
这里写图片描述

条件独立（Conditional Independence）: 若 $P(X,Y,Z)=P(X|Z)P(Y|Z)$ ，称 $X,Y$ 关于 $Z$ 条件独立，记作 $P\models (X\perp Y|Z)$ .
此时以下陈述等价
- $P(X,Y,Z)=P(X|Z)P(Y|Z)$
- $P(X|Y,Z)=P(X|Z)$
- $P(Y|X,Z)=P(Y|Z)$
- $P(Y|X,Z)\propto \phi_1 (X,Z)\phi_2 (Y,Z)$

同理下图表示了 $P(S,G|i^0)=P(S|i^0)P(G|i^0)$ , 计算也可得 $P(S,G|i^1)=P(S|i^1)P(G|i^1)$ . 即 $S,G$ 关于 $I$ 条件独立。
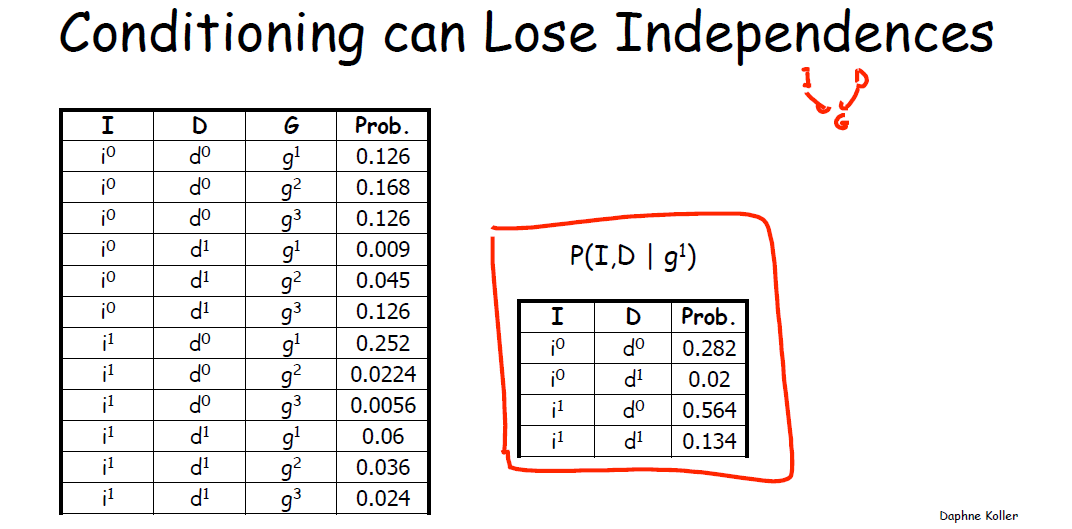
这里写图片描述

4.2 条件独立对于条件的依赖（Conditioning can Lose Independences）

条件独立的成立和某些变量的取值有关，即为“条件”

这部分讨论中间变量被观测与否如何影响了两端变量的独立性，发现条件有时会使变量之间的相关性丧失。上篇博文的 3.1 贝叶斯网络中的独立性和博文概率图模型（PGM）学习笔记（三）模式推断与概率图流中已详细举例讨论，此处继续。
这里写图片描述

　　如图，此处红色笔记内容是 $P \nvDash X_1 \perp X_2$ 和 $P \vDash (X_1 \perp X_2 |C$ ). 其中符号 $\vDash$ 表示“满足”，故上式意为当 Coin 未知时， $X_1$ 和 $X_2$ 条件独立；但当 Coin 的取值已知时， $X_1$ 和 $X_2$ 不条件独立。
　　
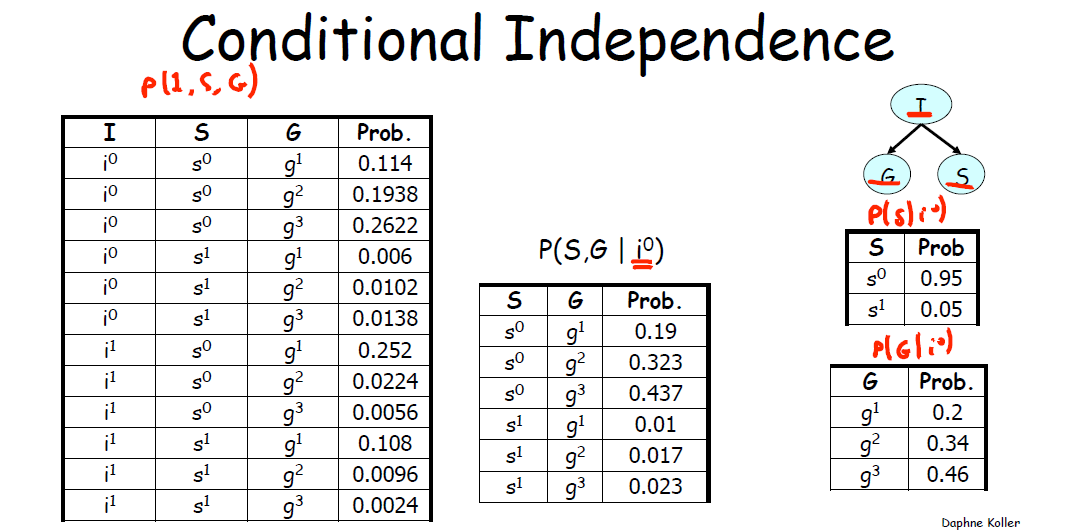
　　具体来说，4.1 中已由下图 $I,D,G$ 联合分布表知道 $P(I,D)=P(I)P(D)$ , 即当 $G$ 未被观测时 $I$ , $D$ 独立。但当讨论限定在 $G$ 上的条件概率分布时，下图数据体现了 $I$ , $D$ 此时（ $G$ 被观测时）不独立。
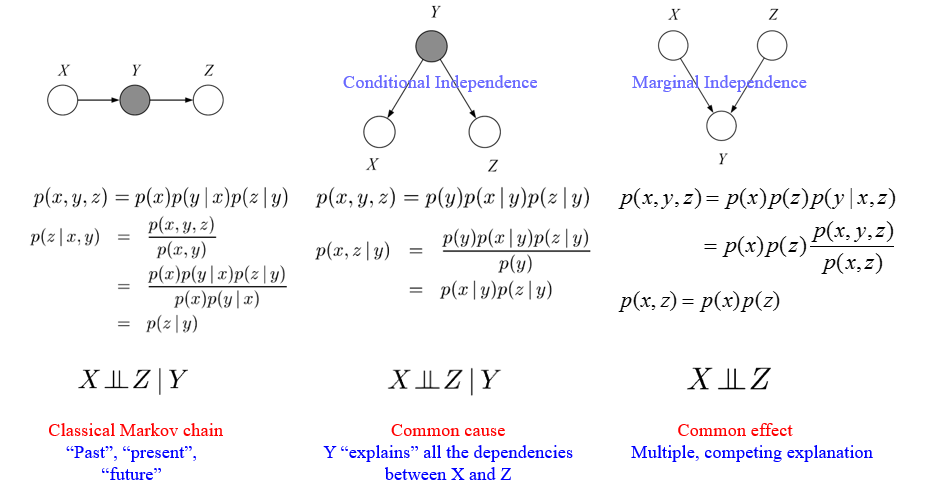
这里写图片描述
　　最后来看对 3 canonical graphs 中的 Conditional Independence1 的解释。

　　图中每个结构都给出了其有条件时的分解和无条件时的分解（这个条件就是要已知它的父节点）。例如，左边第一个结构， $p(x,y,z)$ 是无条件时（ $z$ 的父节点 $x,y$ 未定）的三者联合分布概率，此时无法分解为 $p(x)p(y)p(z)$ ，即不独立。但有条件时 $p(z|x,y)=p(z|y)$ ，即条件独立。
　　总结来说：变量节点会无条件依赖（unconditional dependent）于它的父节点（parent nodes），但是会条件独立（conditionally independent）于它的所有非后裔（nondescendants）节点，这个条件就是要已知它的父节点2。

5. 贝叶斯网中的独立性 ( Independencies in Bayesian Networks )

　　因子分解将分布被表示为因子之积，这与该分布蕴含的独立关系之间有着复杂联系，这是概率图模型最优美的性质之一。我们将讨论：一个分布的因子分解中的因子对应于该分布蕴含的独立性关系。

　　那自然要问：当已知一个分布 $P$ 根据图 $\cal G$ 因子分解时，是否可以从这图的结构中读出该分布蕴含的独立关系？

　　这部分将讨论上述两个问题，介绍 Independence 和 Factorization 两种描述图结构的视角以及两者的等价性。

5.1 d-Separation

　　接着前文（点击这里）关于有效迹（Active Trail）的讨论，我们可以引出 d-分离 (d-Separation) 的概念。
　　直观可以理解为图中不通的两点是 d-分离的，其形式化定义如下

定义 (d-分离) : 若图 $\mathcal G$ 在给定 $Z$ 条件下，节点 $x$ 和 $Y$ 之间不存在任何有效迹，则称 $X$ 和 $Y$ 在给定 $Z$ 时是 d-分离的，记作 $d-sep_{\mathcal G}(X,Y|Z)$ .

定理：若概率图 $\cal G$ 满足 $d-sep_{\mathcal G}(X,Y|Z)$ ，则有 $X$ 与 $Y$ 条件独立，即 $P(X,Y)|Z$ .

　　利用贝叶斯网络链式法则证明如下：（注意由于求的是 $P(I,D)$ ，故求和是对 $G,I,L$ 求和）

这里写图片描述

　　那么什么情况下有“d-Separated”呢？

定理：父节点（parents）已知时，该节点与其所有非后代的节点（non-descendants）满足 d-separated.

　　理解这个定理，看下图。
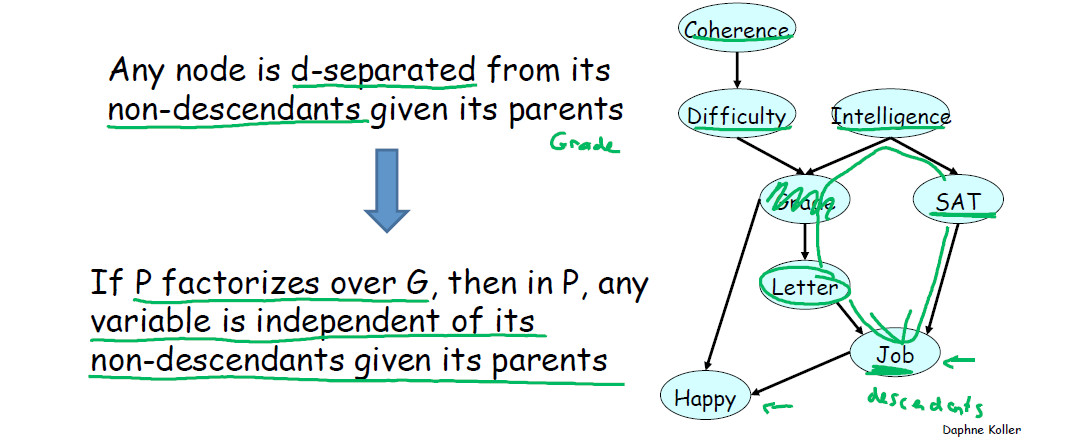
这里写图片描述
　　以 Letter 节点作为例，他的父节点是 Grade，他的子孙是 Job 和 Happy，即 Letter 与其非后代节点 SAT，Intelligence，Difficulty 和 Coherence 满足 d-separated.

5.2 I-maps

　　贝叶斯网的形式化语义是一系列独立性断言（Independences）。同时另一方面，学生例子中的贝叶斯网是由条件概率分布（CPDs）做注释的图，这个图通过链式法则为贝叶斯网定义了一个联合分布。后文我们将证明这两个定义实际上是等价的：分布 $P$ 满足于图 $\mathcal G$ 相关的局部独立性，当前仅当 $P$ 可以由于图 $\mathcal G$ 相关的一系列条件概率分布表示。

　　有了 d-分离的概念，这里引出几个新的定义3：

全局马尔可夫独立性集 : 图 $\cal G$ 的独立性断言之集

定义（全局马尔可夫独立性集）：对于图 $\cal G$ ，定义其与 d-分离相对应的独立性集合为 $I(\mathcal {G})=\{(X \perp Y|Z): d-sep_{\cal G}(X,Y|Z)\}$ ，也称为全局马尔可夫独立性（global Markov independencies）集。

分布 $P$ 的独立性的集合 : 分布 $P$ 的独立性断言之集

定义（独立性集合）: 令 $P$ 是 $\mathcal X$ 上的分布， $\mathcal I(P)$ 定义为在 $P$ 中满足条件独立的所有断言 $(X_i \perp X_j|Z)$ 构成的集合。

I-map：满足分布 $P$ 的独立性要求的图为该分布的 I-map

定义（I-map）: 给定空间 $\mathcal X$ 上的分布 $P$ 的和其独立性集合 $\mathcal I(P)$ ，如果贝叶斯网络 $\cal G$ 能满足 $\mathcal I(P)$ 的独立性要求，即 $\mathcal I( \mathcal G) \subseteq I(P)$ ，则称 $\cal G$ 是 $P$ 的一个 I-map.

我们将这个定义通俗理解为：满足分布 P 的独立性要求的图为该分布的 I-map.

I-等价：两个图 I-等价即两者独立性集合完全相同.
一组简单的例子解释 I-maps. 考虑定义在 $G,I$ 上三种个可能的图：
- $\mathcal G_{\varnothing}$ （下图的 $G_1$ ，无连接的边）；
- $\mathcal G_{D \rightarrow I}$ （下图的 $G_2$ ，包含一条从 $D$ 到 $I$ 的迹）；
- $\mathcal G_{I \rightarrow D}$ （包含一条从 $I$ 到 $D$ 的迹，结构与 $G_2$ 相同，故不赘述）。

考虑如下两个分布 $P_1$ 和 $P_2$ .
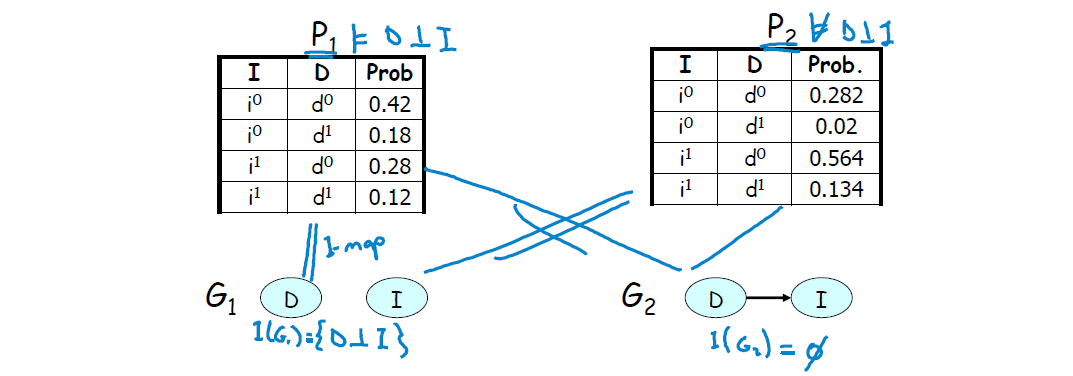
这里写图片描述
　　左例：表格可知 I, D 独立，则 $P_1$ 的独立性关系有 ${D\perp I}$ . 又由于 $\mathcal I(\mathcal　G_{\varnothing})={D\perp I}$ ，因此 $\mathcal I(\mathcal　G_{\varnothing})\in \mathcal I(P_1)$ ，有 $\mathcal　G_{\varnothing}$ 是 $P_1$ 的 I=Map。同理有 $\mathcal I(\mathcal　G_{D \rightarrow I}), I(\mathcal　G_{I \rightarrow D})\in \mathcal I(P_1)$ ，即 $\mathcal G_{D \rightarrow I}$ 和 $\mathcal G_{I \rightarrow D}$ 也是 $P_1$ 的 I-map.

　　右例：表格可知 I, D 不独立，则图 $P_2$ 的两个变量（即该图的所有变量）无独立性关系，故为空集，即 $\mathcal I(P_2)={\varnothing }$ . 故 $\mathcal G_{\varnothing}$ 不是 $P_2$ 的 I-map.

5.3 Independence 和 Factorization 的等价性

　　现在我们可以回到本节开始提出的两个问题了：

　　1）一个分布的因子分解和该分布蕴含的独立性关系有何联系？
　　2）当已知一个分布 $P$ 根据图 $\cal G$ 因子分解时，是否可以从这图的结构中读出该分布蕴含的独立关系？

　　对于问题1），我们得到一个优美的结论，即因子分解与独立关系这一组双重对偶视角的统一性。陈述如下

Independence 和 Factorization 的等价性
- 如果独立的概率分布 $P$ 可以按照某个图 $\mathcal G$ 分解，那么 $\mathcal G$ 就是 $P$ 的一个 I-map；
- 反之，如果 $\mathcal G$ 是概率分布 $P$ 的一个 I-map，那么 $P$ 可以按照 $\mathcal G$ 来进行分解。

这里写图片描述

从 Independence 和 Factorization 2 个观点来看，我们得到了概率图的两种等价的观点（双重对偶视角）：

1 ) 概率图 $\mathcal G$ 是用来表示概率分布 $P$ 的（Factorization: G allows $P$ to be reprensented）;
2 ) $P$ 是用来表达概率图 $\mathcal G$ 所展示的独立关系的（I-map: Independencies that encoded by $\mathcal G$ hlod in $P$ ）。

对于问题2）：If P factorizes over a graph $\mathcal G$ , we can read from the graph independencies that must hold in $P$ (an Independency Map).

　　可以理解为：当已知一个分布 $P$ 根据图 $\cal G$ 因子分解时，确实可以从这图的结构中读出该分布蕴含的独立关系。但是，不能保证读出分布中的所有独立性关系。
　　这一点从 I-map 的定义就可以理解，因为定义中只要求 $\mathcal I( \mathcal G) \subseteq I(P)$ ，而不是 $\mathcal I( \mathcal G) = \mathcal I(P)$ 。后面我们会讨论到满足 $\mathcal I( \mathcal G) = \mathcal I(P)$ 的 P-map 及其存在唯一性问题。讲到马尔可夫网（MN）时，我们将对MN 讨论相同的两个问题，并深入讨论何时可以找到一个图来恰好完美捕捉分布中的所有独立性。推荐

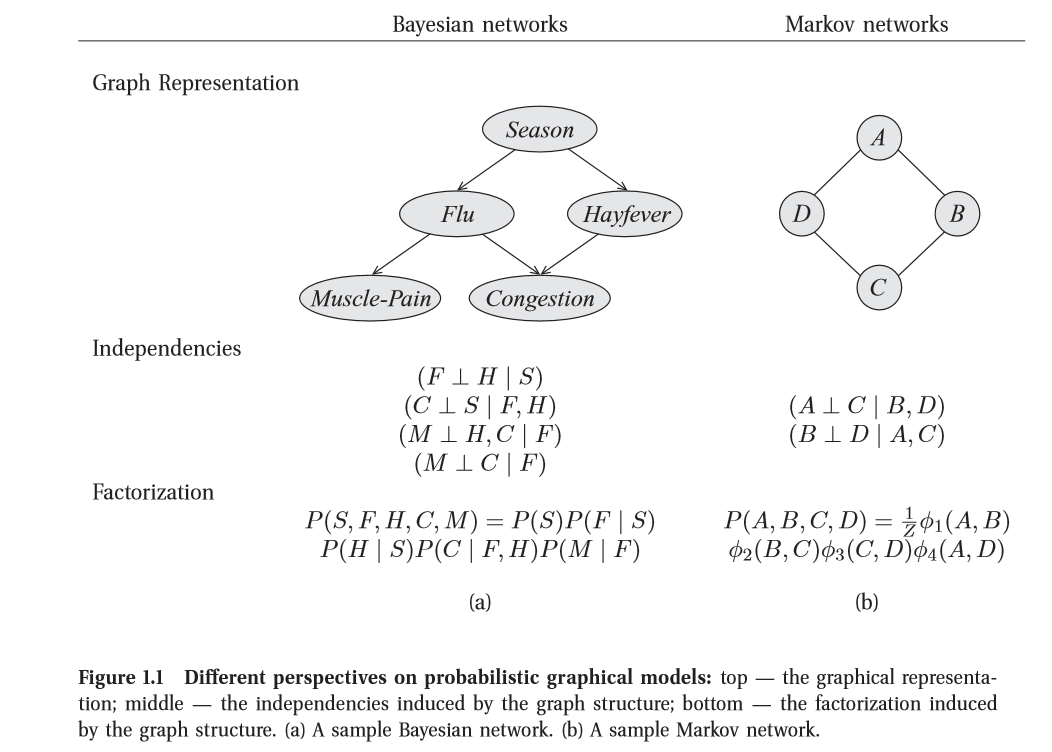
Koller 在书中开篇4对两者等价性做以陈述如下（这部分作为简单补充，可忽略）

这里写图片描述

　　分别解析两种视角（perspectives）

独立关系（Independence）

　　图是在分布中蕴含的独立关系集合的一个紧凑表示：对于一组变量 $X,Y,X$ 而言，这些关系成为“给定 $Z$ 时，变量 $X$ 和 $Y$ 独立，记作 $X \perp Y|Z$ ”;

因子分解（Factorization）

　　图定义了紧凑表示高纬分布的一种框架：与其对图中所有变量可能取值的概率进行编码，不如将分布“分解”为些更小的因子，使每一个因子定义在更小的概率空间上。然后，我们可以将总体的联合分布定义为这些因子的乘积。

　　结果是这两种视角一一图作为独立关系集合的表示与图作为分解分布的框架一一在深层意义上是等价的。准确地说，正是分布的独立特性才使得分布能够紧凑地以因子分解的形式表示。反之，分布的一个特别的因子分解确保了某些独立关系的成立。
- Independence

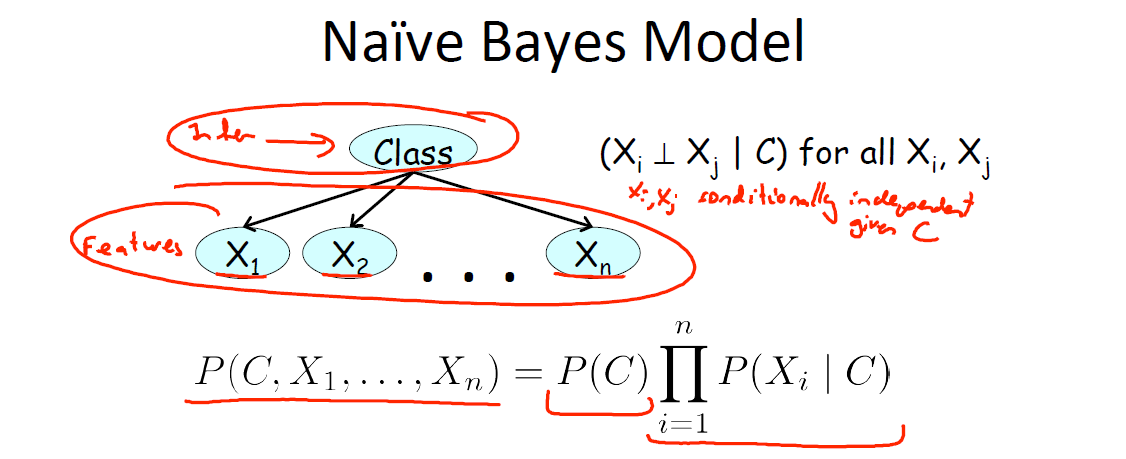
6. 朴素贝叶斯 ( Naive Bayes )

　　这部分介绍朴素贝叶斯模型。这里举一个例子，方便后文对概念的解释。
　　简化学生例子：考虑在 $S,I,G$ 上的联合分布，其含义和关系同前文的学生例子（见学生例子），即 $G \leftarrow I \rightarrow S$ 。

6.1 独立性假设

　　Naive Bayes，也称作 Idiot Bayes，朴素贝叶斯模型假设所有的事例属于若干两两互斥且包含所有事例情况的类（class）中的一个6。因此存在在某一个集合 ${c_1,...,c_n}$ 中取值的类变量 $C$ 。简化学生例子中，类变量是学生智商 $I$ ，并且存在事例的两个类——高智商（smart）和低智商（stupid）。同时，模型还包括一定数量的、可以观测到值的特征（features）。

独立性假设: 朴素贝叶斯模型假设在给定的事例的类的条件下，这些特征均为条件独立的。

　　换言之，在事例的每一个类汇总，不同的性质可以独立的确定，形式化表述为：对于任意的 $i,j$ 有 $(X_i \perp X_j|C).$
这里写图片描述

6.2 两种贝叶斯分类器：伯努利和多项式

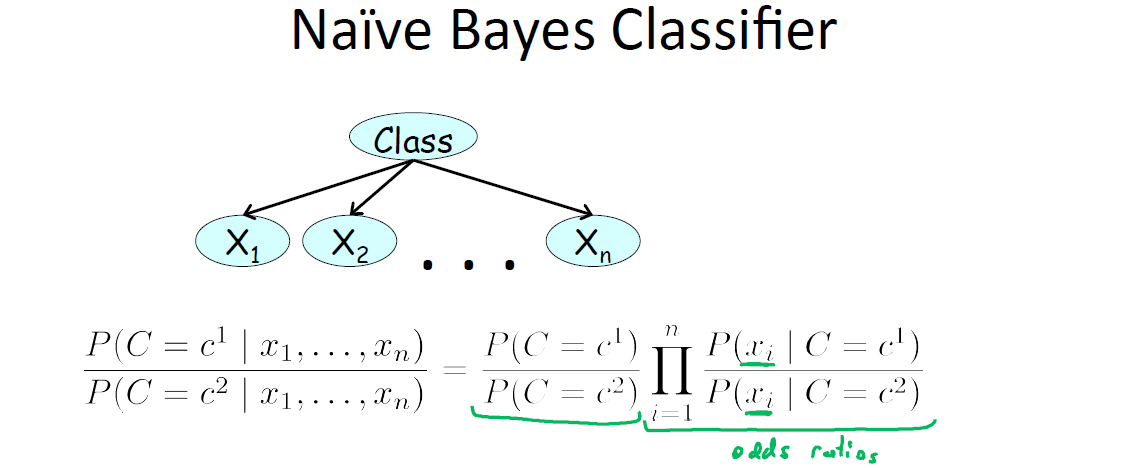
这里写图片描述
　　朴素贝叶斯分类器，此处介绍常用的两种：伯努利朴素贝叶斯和多项式朴素贝叶斯。首先明确伯努利分布和多项式分布。

设随机变量 $X$ 的所有取值为 $x \in Val(X)$ ，设 $k=|Val(X)|$ ，则当讨论对 $X$ 取特殊值的枚举时，有陈述 $\sum^k_{i=1}P(X=x_i)=1$ .

　　这种变量上的分布成为多项式分布（multinomial distribution）。对于二值随机变量， $Val(X)=\{ture, false\}$ ，这种随机变量的分布成为伯努利分布。

　　接下来来看两种朴素贝叶斯分类器在文本分类中的应用7：
　　(1)伯努利：每个单词分配一个CPD，即每个单词在每个文本分类中出现的概率；
　　(2)多项式：每个单词位置分配一个CPD，即每个位置上不同文本分类出现特定单词的概率，每个位置上给定文本类别出现特定单词概率之和为1。
　　
　　详细解释如下：

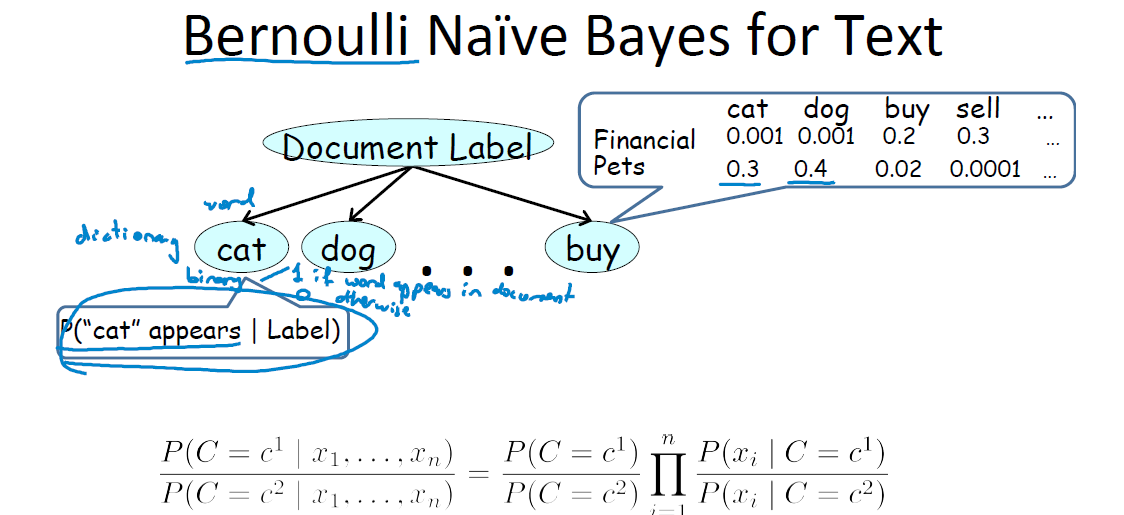
伯努利朴素贝叶斯

这里写图片描述

　　这种方式实质上是“查字典”，它把cat、dog、buy这些当做字典里的词目。之所以称为“伯努利”是因为，这种方式只管分析文章里面有没有出现词典里的词目，而不管出现了多少次。词典的条目都是只有 0-1 的二项分布随机变量。
　　文档属于这两类的概率分别为上图最后一行的公式。每一个小乘积项代表了“如果这是一篇财务文档，能出现cat字眼的概率是0.001”这样的意义。
　　为什么说是“朴素”了，因为它假设了每个词的条目出现是相互不影响的（事实上这个在真实的语言学中是不成立的8，联系“二八定律”），即有 $X_i \perp X_j$ for all $X_i, X_j$ .

幂律分布中的二八定律：可以在莎士比亚的作品中找到词和词频之间的幂律关系。20%的词用掉了80%的篇幅。这就是经常说的2-8定律，这个定律只是近似的标示分配的不平均，而并不是定量的分析.

为什么莎翁的作品中出现幂律分布？
1. 样本间相互不独立是幂律生成的重要条件。
2. 莎士比亚作品英文原著的分析发现存在幂律，但如果分析中文翻译版中以字为单位去研究，幂律就消失了，只有把翻译版中的词做研究单位幂律才会重新出现。
3. 词能出现幂律是因为有语法结构把词联系在一起，而字的联系却没有这么紧密。
4. 现代文学作品中以词为单位统计词频会出现幂律，以字为单位统计字频不会出现幂律，先秦文学作品中以字为单位统计字频会出现幂律，原因在于古汉语中一个字就代表一个词的现象很普遍。

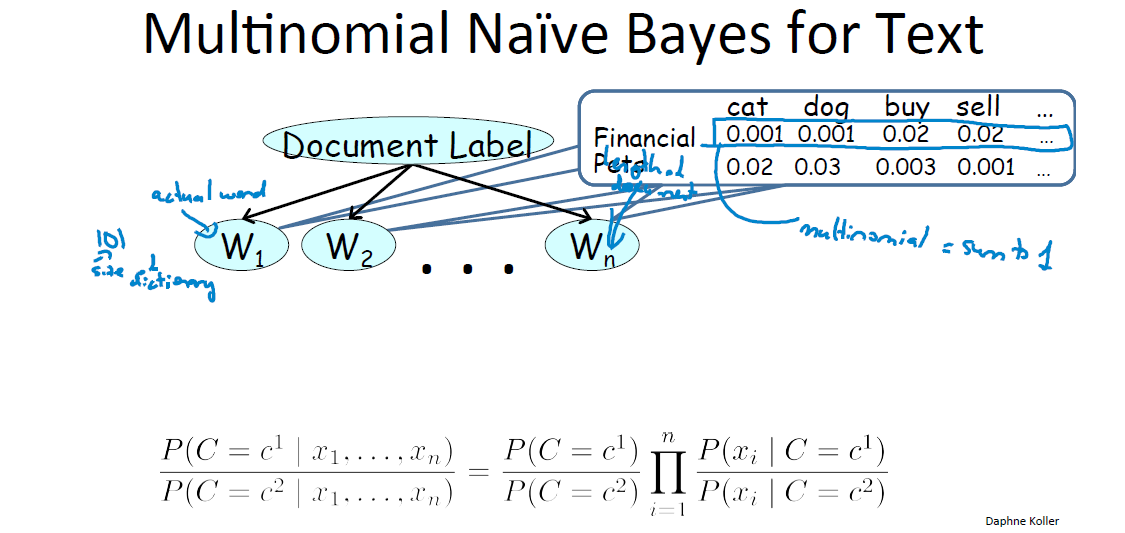
多项式朴素贝叶斯

这里写图片描述

　　这种方式与伯努利有本质不同。W这些单元再也不是词典的条目了，而是待分类文章中的真实单词。假如这篇文章写了1991个词，那么就有1991个W。
　　文档属于这两类的概率依然为上式。每一个小乘积项代表了“如果这是一篇财务文档，在文章里任意一个位置出现cat的概率是0.001”这样的意思。表还是那张表，但是意思现在完全不一样了，因为现在要求 cat+dog+buy+sell 这些概率加起来要等于1。而伯努利没这个限制，随意等于多少。这个区别很重要。
　　为什么这个贝叶斯也是朴素的呢？因为它假定了在文章所有位置出现cat的概率是满足同样的分布的。但我们应该注意到，实际上这也是一个很弱的假设，就像类似“敬爱的”这样的问候语必然一般都会出现在开头。

朴素贝叶斯分类器优势总结

这里写图片描述

7. Application - Medical Diagnosis

最后，看懂了这些后再去看王钰前辈的 PPT 结构+平均-读 Daphne Koller的“概率图模型”9会觉得十分清晰。

Weike Pan, Congfu Xu. 浙江大学计算机学院《人工智能引论》课件, Chapter 10 Introduction to Probabilistic Graphical Models. ↩
概率图模型（PGM）里的的条件独立（conditional independent）. ↩
王飞跃, 韩素青译. 概率图模型 - 原理与技术, 清华大学出版社, 2015: page 70-71. ↩
Daphne Koller, Nir Friedman. Probabilistic Graphical Models - Principles and Techniques, 2009: page 4. ↩
ycheng_sjtu, 概率图模型（PGM）学习笔记（四）-贝叶斯网络-伯努利贝叶斯-多项式贝叶斯. ↩
王飞跃, 韩素青译. 概率图模型 - 原理与技术, 清华大学出版社, 2015: page 50. ↩
概率图模型笔记(2)——Bayesian Network Fundamentals. ↩
卓老板聊科技, 喜马拉雅, [S2] 016 为什么20%的人占据80%的财. ↩
王钰, 结构+平均-读 Daphne Koller的“概率图模型”. ↩