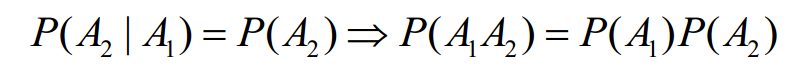分类加法，分步乘法

1. 分类加法计数原理场景：从甲地到乙地，可以乘火车、汽车、轮船。火车有 4 班、汽车 2 班、轮船 3 班，那么一天中乘坐这些交通工具从甲地到乙地有多少种不同的走法？
2. 分步乘法计数原理场景：从 A 到 B 的道路有 3 条，从 B 到 C 的道路有 2 条，那么从 A 到 B 到 C 总共有多少种不同的走法？

区别：分类计数原理是加法原理，不同的类加起来就是我要得到的总数；分步计数原理是乘法原理，是同一事件分成若干步骤，每个步骤的方法数相乘才是总数。

排列问题

从n个不同元素种取出m(m≤n)个元素的所有不同排列的个数，叫做从n个不同元素种取出m个元素的排列数，用符号 $A_n^m$ 表示。

$A_n^m=n(n-1)(n-2)\cdots(n-m+1)=\frac{n!}{(n-m)!}$

推导：把n个不同的元素任选m个排序，按计数原理分步进行

取第一个：有n种取法；
取第二个：有(n−1)种取法；
取第三个：有(n−2)种取法；
……
取第m个：有(n−m+1)种取法；

根据分步乘法原理，得出上述公式。

组合问题

从n个不同元素种取出m(m≤n)个元素的所有不同组合的个数，叫做从n个不同元素种取出m个元素的组合数，用符号 $C_n^m$ 表示。

$C_n^m=\frac{A_n^m}{A_m^m}=\frac{n(n-1)(n-2)\cdots (n-m+1)}{m!}=\frac{n!}{m!(n-m)!}$

为什么要除以 $A_m^m$ ，因为要去除重复， $A_m^m$ 代表把这m个被抽出来的球进行全排序，除代表这么多种的排列组合都代表一个情况(因为组合 $C_n^m$ 是没序的)

等可能概率(古典概型)

定义：若试验满足：
样本空间S中样本点有限(有限性)
出现每一个样本点的概率相等(等可能性)
称这种试验为等可能概型(或古典概型)。

条件概率

全概率公式

贝叶斯公式

先验后验

这是与贝叶斯概率更新有关的两个概念。假如某一不确定事件发生的主观概率因为某个新情况的出现而发生了改变，那么改变前的那个概率就被叫做先验概率(上面公式的Bi)，改变后的概率就叫后验概率(上面公式的P(Bi|A) )。

举个简单的更新概率的例子。
想象有 A、B、C 三个不透明的碗倒扣在桌面上，已知其中有（且仅有）一个瓷碗下面盖住一个鸡蛋。此时请问，鸡蛋在 A 碗下面的概率是多少？答曰 1/3。
现在发生一件事：有人揭开了 C 碗，发现 C 碗下面没有蛋。此时再问：鸡蛋在 A 碗下面的概率是多少？答曰 1/2。注意，由于有“揭开C碗发现鸡蛋不在C碗下面”这个新情况，对于“鸡蛋在 A 碗下面”这件事的主观概率由原来的 1/3 上升到了1/2。这里的先验概率就是 1/3，后验概率是 1/2。
也就是说“先”和“后”是相对于引起主观概率变化的那个新情况而言的。

事件独立

推导理解：

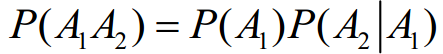
因为A1的发生对A2的发生概率不影响

统计学条件概率、贝叶斯公式