一、TL;DL
条件概率的公式:P(AB)=P(A)P(B|A)=P(B)P(A|B);即事件A和事件B同时发生的概率等于在发生A的条件下B发生的概率乘以A的概率。
贝叶斯公式:由条件概率公式推导出 P(B|A)=P(A|B)P(B)/P(A)
全概率公式:假设B是由相互独立的事件组成的概率空间{B1,b2,...bn},P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+..P(A|Bn)P(Bn)
两个事件的独立性:意味着P(A|B)=P(A);P(AB)=P(A|B)P(B)=P(A)P(B)
结合全概率公式后,贝叶斯公式:
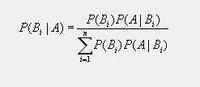
常常把P(Bi|A)称作后验概率(Posterior),而P(A|Bn)P(Bn)为先验概率(Prior)。而P(Bi)又叫做基础概率。
多元贝叶斯:P(A|B,C) = P(A,B,C)/P(B,C)= P(C|A,B)*P(A,B)/P(B,C) = P(C|A,B)*P(B|A)*P(A)/P(C|B)*P(B)
联合概率分布(joint probability distribution):同时考虑多个随机变数的概率分布
贝叶斯网络:贝叶斯信念网络或有向无环图模型,是一种概率图模型
二、贝叶斯法则
在贝叶斯法则中,每个名词都有约定俗成的名称:
Pr(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
Pr(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
Pr(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
Pr(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)。
按这些术语,Bayes法则可表述为:
后验概率 = (似然度 * 先验概率)/标准化常量 也就是说,后验概率与先验概率和似然度的乘积成正比。
另外,比例Pr(B|A)/Pr(B)也有时被称作标准似然度(standardised likelihood),Bayes法则可表述为:
后验概率 = 标准似然度 * 先验概率
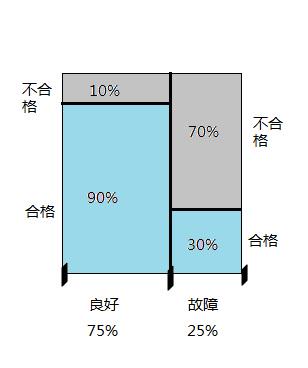
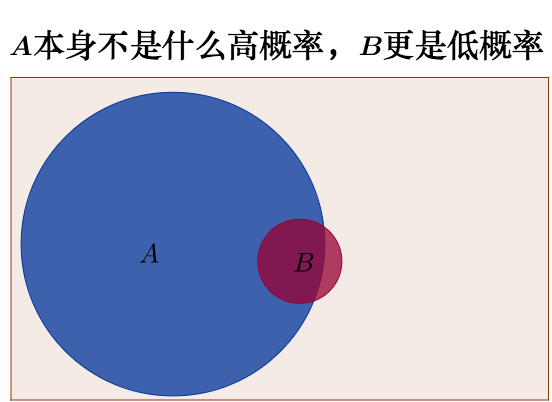
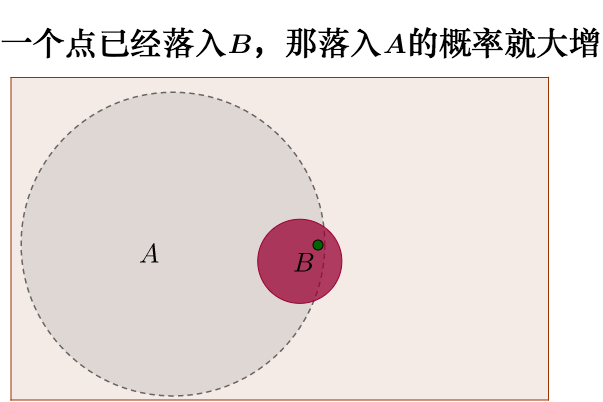
直观理解贝叶斯原理:
|
|
|
三、全概率公式
B_i之间两两互斥且在每次试验中至少发生其中一个(互相独立),计算A可以使用全概率公式,从对B的条件概率入手

P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+..P(A|Bn)P(Bn)
四、贝叶斯网络
贝叶斯网络(Bayesian network),又称信念网络(Belief Network),或有向无环图模型(directed acyclic graphical model),是一种概率图模型。它是一种模拟人类推理过程中因果关系的不确定性处理模型,其网络拓朴结构是一个有向无环图(DAG)。
贝叶斯网络中的节点表示随机变量,有向边表示变量之间有因果关系(非条件独立),两个用箭头连接的节点就会产生一个条件概率值。
A Bayesian network is a directed graph in which each node is annotated with quantitative probability information. The full specification is as follows:
A set of random variables makes up the nodes of the network. Variables may be discrete or continuous.
A set of directed links or arrows connects pairs of nodes. If there is an arrow from node X to node Y, X is said to be a parent of Y
Each node X_i has a conditional probability distribution P(Xi| Parents(Xi)) that quantifies the effect of the parents on the node.
The graph has no directed cycles (and hence is a directed, acyclic graph, or DAG).
许多经典的多元概率模型都是贝叶斯网络的特例,例如朴素贝叶斯模型、马尔科夫链、隐马尔科夫模型、卡尔曼滤波器、条件随机场等等。
1.概率流动的影响性
概率流动的影响性(Flow of Probabilistic Influence)指的是在一定的观测条件下,变量间的取值改变是否会有相互影响,这里给出两个概念:
观测变量:变量取值可观测,或变量取值已经确定
隐变量:变量取值未知,通常根据观测变量的取值,对隐变量的取值概率进行推理。
1.1独立的概念
变量独立性
随机变量X,Y若满足如下关系中的任意一个:
P ( X , Y ) = P ( X ) P ( Y )
P ( X ∣ Y ) = P ( X )
P ( Y ∣ X ) = P ( Y )
那么我们就称随机变量X和Y相互独立
条件独立性
随机变量X,Y在Z给定条件下满足:
P ( X , Y ∣ Z ) = P ( X ∣ Z ) P ( Y ∣ Z )
P ( X ∣ Y , Z ) = P ( X ∣ Z )
P ( Y ∣ X , Z ) = P ( Y ∣ Z )
那么我们同样可以认为随机变量X和Y满足独立关系。
2. 4种经典的信息流动结构
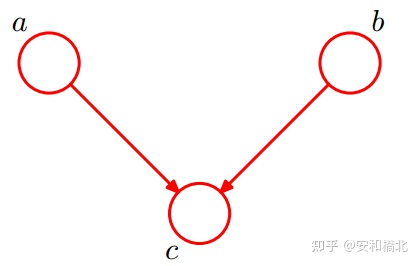
3. 贝叶斯网络中的条件独立关系
3.1 d-separation
3.2 d分离的推论
A node is conditionally independent of its non-descendants, given its parents.
A node is conditionally independent of all other nodes in the network, given its parents, children, and children's parents - that is, given its Markov blanket.
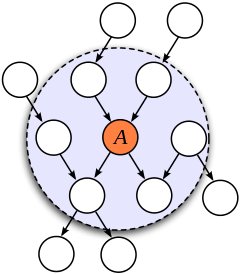
Markov Blanket
五、贝叶斯应用
数学领域 |
▪ 贝叶斯分类算法 (应用:统计分析、测绘学) ▪ 贝叶斯公式 (应用:概率空间) ▪ 贝叶斯区间估计 (应用:数学中的区间估计) ▪ 贝叶斯序贯决策函数 (应用:统计决策论) |
▪ 贝叶斯风险 (应用:统计决策论) ▪ 贝叶斯估计 (应用:参数估计) ▪ 贝叶斯统计 (应用:统计决策论) ▪ 经验贝叶斯方法 (应用:统计决策论) |
工程领域 |
▪ 贝叶斯定理 (应用:人工智能、心理学、遗传学) ▪ 贝叶斯分析 (应用:计算机科学) ▪ 贝叶斯逻辑 (应用:人工智能) ▪ 贝叶斯网络 (应用:人工智能) |
▪ 贝叶斯分类器 (应用:模式识别、人工智能) ▪ 贝叶斯决策 (应用:人工智能) ▪ 贝叶斯推理 (应用:数量地理学、人工智能) ▪ 贝叶斯学习 (应用:模式识别) |
其他领域 |
▪ 贝叶斯主义 (应用:自然辩证法) |
▪ 有信息的贝叶斯决策方法 (应用:生态系统生态学) |