神经网络学习——BP神经网络笔记

神经网络学习，又叫做神经网络的训练算法，可以通过计算和更新神经网络本身的权值和阈值，加强网络自身的学习能力。

一.神经元模型

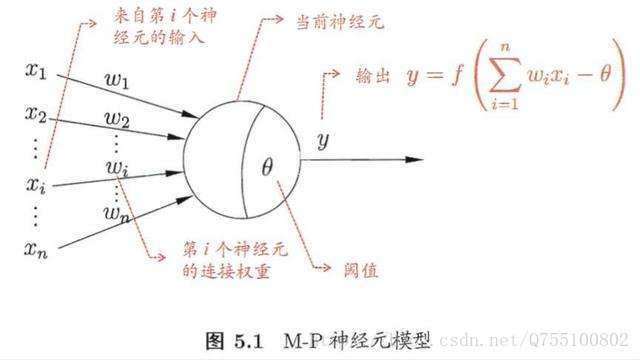
        神经网络最基本的模型就是神经元模型，也是神经网络中的简单单元。神经元常用的简单模型是M-P神经元模型，如下所示：

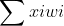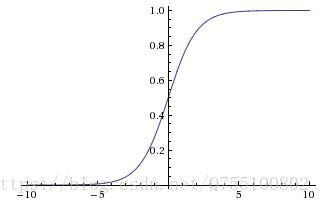
阈值：就相当于神经元的兴奋电位，当这个神经元的输入电位大于这个神经元的阈值时，它就会被激活，向其他神经元发送电位，所以输出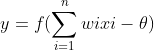,而函数f表示的是一个激活函数，它将函数的输出值挤压到（0,1）的范围之内，函数图像如下

其他常用的也有符号函数什么的，不过不够光滑。

为了简化表示，通常我们把阈值 θ记为 −w0，并假想有一个附加的常量输入 x0=1，那么我们就可以把神经元的输入记为 ∑ni=0wixi 或以向量形式写为 w⋅x，把输出记为 y=f(∑ni=0wixi)。

把许多个这样的神经元按一定层次组合，就得到一个神经网络。

二.感知机

        感知机由两层神经元组成，输入层接受外部信号后传给输出层，输出层就是M-P神经元，亦称“阈值逻辑单元”，由阈值的大小将输入的数据分为多种逻辑组合。感知机的激活函数 ff 就是之前介绍过的阶跃函数，因而我们可以把感知机函数写为

                                                                          

y=sgn(x)就是我们熟悉的符号函数。还可以把感知机看作是 n 维实例空间中的超平面决策面，对于超平面一侧的实例，感知器输出 1，对于另一侧的实例输出 0，这个决策超平面方程是 w⋅x=0。 那些可以被某一个超平面分割的正反样例集合称为线性可分(linearly separable)样例集合，它们就可以使用感知机表示。

        所以，给定训练集，感知机的权重wi和阈值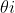就可以通过学习得到。由上述可以阈值也可以当做一个-1w0的权值，所以学习过程就可以统一为权值的学习。学习规则非常简单，对训练样本(x,y)，若当前感知机输出为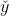，则调整公式如下：

                                                      

                                                                          

其中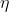，为学习率，若感知机预知正确，则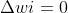，感知机不发生变化，否则将根据错误的程度进行权重调整。

        从上面的知识知道，感知机只有一层功能神经元（所谓功能神经元，就是有阈值的神经元，输入层是没有阈值的），学习能力差，只能解决线性问题，甚至不能求解异或这样的非线性可分的问题。

        要解决非线性可分的问题，需要使用多层功能神经元，所以在输入层和输出层之间通常会加入一层或多层隐含层，隐含层和输出层都是具有激活函数和阈值的功能神经元。更一般的，常见的神经网络是如下图所示的层次结构，神经元之间不存在同层连接，也不能跨层连接，这样的神经网络通常被称为多层前馈神经网络。

        单隐层的神经网络是最常见的神经网络，我们的BP神经网络就是这种。已经证明，只需一个包含足够多的神经元的隐层，多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数，虽然我不知道也不关心怎么证明的，然而个数的设置仍是未解问题，还得靠试错法调整。

三.误差逆传播算法——BP算法

        这是一种典型的有导师指导的学习算法，基本思想就是对一定数量的样本对（输入和期望输出）进行学习，即将样本的输入传入送至网络输入层的各个神经元，经隐含层和输出层计算后，输出层各个神经元输出对应的预期值，若预期值与期望的输出之间不满足误差精度要求，则从输出层反向传播该误差（注意传播的是误差），并通过权值和阈值的修改公式进行修改，使得整个网络的输出和期望输出的误差不断减小，直到满足精度为止。

        也就是说，BP网络是将网络的输出与期望输出间的误差归结为权值和阈值的过错，反向传播将误差分摊给各个功能神经元，权值和阈值的调整也要沿着误差函数下降最快的方向——负梯度方向进行调整，调整公式就是重中之重。

        给定一个样本矩阵，，并且有一个拥有d个输入神经元，l个输出神经元，q个隐层神经元的多层前馈神经网络结构，输出层第j个神经元的阈值

为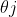，隐含层阈值为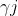；输入层与隐含层的神经元连接为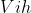，隐含层与输出层的神经元连接为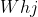，则隐含层第h个神经元的输入为

                                                                    

输出层第j个神经元接收到的输入为

                                                                     

Bh为隐层第h个神经元的输出。对训练例（xk,yk），假定神经网络的输出为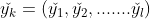

即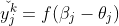                                               

则网络在（xk,yk）上的均方误差为

                                                                      

这个就是我们要缩小和反向传播的误差值，BP是一个迭代学习算法，在迭代的每一轮中采用广义的感知机学习规则对参数进行更新和评估，所以，任意参数的更新公式都为

                                                                       

BP算法基于梯度下降策略，以目标的负梯度方向对参数进行调整，对误差Ek,给定学习率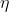，有

                                                                       

注意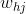，先影响到第j个输出层神经元的输入值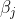，再影响到其输出值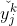，然后影响到Ek，这就是整个误差逆传递的过程，有

                                                                       

而

                                                                       

且

                                                                       

所以有

                                                                       

所以联立几个式子，有

                                                                       

类似的，所有阈值和权值的更新公式都可以由上述的近似方法得到，有

                                                                       

                                                                       

                                                                        

其中，

                                                                        

  所以，我们得到整个BP神经网络的计算过程

  输入：训练集D=（xk,yk），学习率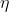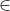(0,1)

  过程：

          1.在(0,1)范围内随机初始化网络中所有连接权和阈值

          2.repeat

          3.      for all (xk,yk)

          4.             根据当前参数和式（5.3）计算当前样本的输出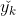

          5.             根据式（5.10）计算输出层神经元的梯度项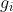

          6.             根据式（5.15）计算隐含层神经元的梯度项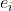

          7.             根据式（5.11）-（5.14）更新连接权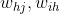与阈值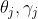

          8.      end for

          9. until   达到停止条件

 输出：连接权与阈值确定的多层前馈神经网络

 具体实例和代码，就等到下篇文章再记吧~

注：参考资料：《机器学习》周志华