简介
误差反向传播算法简称反向传播算法(即BP算法)。
使用反向传播算法的多层感知器又称为BP神经网络。BP算法是一个迭代算法,它的基本思想为:
-
1、先计算每一层的状态和激活值,直到最后一层(前向传播)
-
2、计算每一层的误差,误差的计算过程是从最后一层向前推进的
-
3、更新参数(目标是误差变小)。迭代前面两个步骤,直到满足停止准则(比如相邻两次迭代的误差的差别很小)
本文约定
对于M-P神经元和感知机(简单的前馈神经网络)都在上一篇博文中介绍了,现在先规定一下下面讲解推到过程的时候的一些记号
-
n l \ n_l nl表示第 l \ l l层的神经元个数
-
f ( ⋅ ) \ f(·) f(⋅) 表示神经元的激活函数(激活函数我另外会再开一篇博文来记录)
-
W ( l ) ∈ R n l × n l \ W^{(l)} \in \mathbb{R}^{n_l \times n_l} W(l)∈Rnl×nl 表示第 l − 1 \ l-1 l−1 层到第 l \ l l 层的权重矩阵
-
w i j ( l ) \ w^{(l)}_{ij} wij(l)表示第 l \ l l层的第 j \ j j个神经元与上一个,即 ( l − 1 ) \ (l-1) (l−1)层的第 i \ i i个神经元的连接权重
-
b i ( l ) \ b^{(l)}_i bi(l)表示第 l \ l l层的第 i \ i i个神经元的偏置
-
b ( l ) = ( b 1 ( l ) , b 2 ( l ) , . . . , b n l ( l ) ) T ∈ R l n \ b^{(l)} = (b^{(l)}_1, b^{(l)}_2,...,b^{(l)}_{n_l})^T\in\mathbb{R}^n_l b(l)=(b1(l),b2(l),...,bnl(l))T∈Rln表示第 l − 1 \ l-1 l−1层到第 l \ l l层的偏置
-
z i ( l ) \ z^{(l)}_i zi(l) 表示第 l \ l l层中第 i \ i i个神经元节点的输入值
-
z ( l ) = ( z 1 ( l ) , z 2 ( l ) , . . . , z n l ( l ) ) T ∈ R l n \ z^{(l)} = (z^{(l)}_1, z^{(l)}_2,...,z^{(l)}_{n_l})^T\in\mathbb{R}^n_l z(l)=(z1(l),z2(l),...,znl(l))T∈Rln表示第 l − 1 \ l-1 l−1层到第 l \ l l层的输入
-
a i ( l ) \ a^{(l)}_i ai(l)表示第 l \ l l层中第 i \ i i个神经元节点的激活值(输出值)
使用的图片来源网络,部分符号约定不同自行变通
本文以三层感知机为例

信息前向传播
由该神经网络可以得出第二层的参数
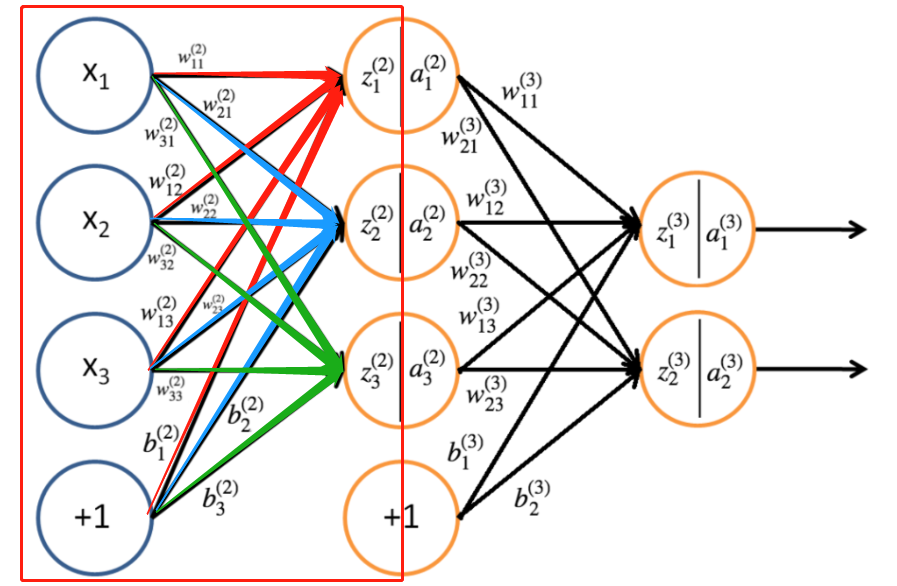
并且,我们能够用相同的方法计算第三层的参数
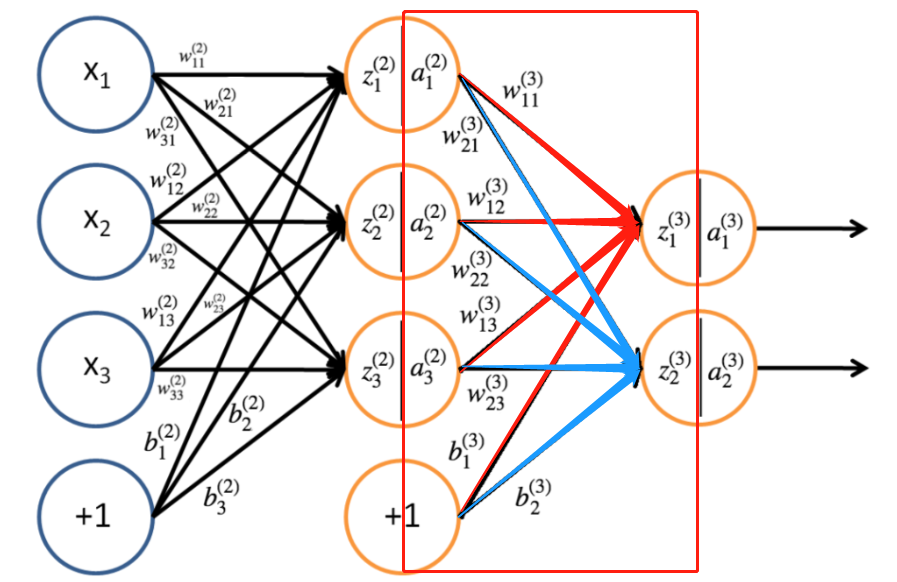
所以可以总结出,第 l ( 2 ≤ l ≤ L ) \ l(2\leq l \leq L) l(2≤l≤L) 层神经元的输入和激活值(输出值)
所以对于前馈神经网络的信息前向传播的传递过程入下:
误差反向传播
目的:调整 w 、 b \ w 、 b w、b权重和偏置直到最优,知道损失函数最小为止
使用方法:梯度下降法(本文使用批量梯度下降、随机梯度下降)
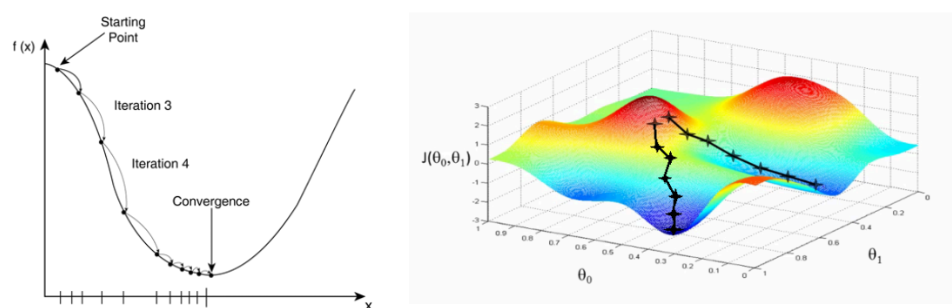
权重和偏置的更新规则为:
-
w n e w 、 w o l d \ w_{new}、w_{old} wnew、wold 表示该连接的新权重和旧的权重
-
b n e w 、 b o l d \ b_{new}、b_{old} bnew、bold 表示该连接的新偏置和旧的偏置
-
J t o t a l \ J_{total} Jtotal表示每个 ( x ( i ) , y ( i ) ) \ (x_{(i)},y_{(i)}) (x(i),y(i)) 数据计算出的损失函数的平均
μ \ \mu μ 代表学习率,即“步长”
下面我们求损失函数(本文使用平均损失,交叉熵损失函数暂无)
对于训练数据为 ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . , ( x ( N ) , y ( N ) ) \ {(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(N)},y^{(N)})} (x(1),y(1)),(x(2),y(2)),...,(x(N),y(N))即总共由 N \ N N组训练数据(不含测试数据),所以它最后的输出的训练实际值就有 y ( i ) = ( y 1 ( i ) , ⋅ ⋅ ⋅ , y n L ( i ) ) T \ y^{(i)} = (y^{(i)}_1,···,y^{(i)}_{nL})^T y(i)=(y1(i),⋅⋅⋅,ynL(i))T
对于某一个数训练数据 ( x ( i ) , y ( i ) ) \ (x^{(i)},y^{(i)}) (x(i),y(i))来说就有一个损失函数:
-
y ( i ) \ y^{(i)} y(i)代表期望的输出,也就是我们自己给出的数据中的 y \ y y值
-
o ( i ) \ o^{(i)} o(i) 为网络的实际输出
所以一个epoch下来,的平均损失:
输出层权重更新
还是用本文前那个神经网络进行示例进行输出层权重的更新
$\ J_{(3)} = \frac{1}{2}\parallel y{(3)}-o{(3)}\parallel \ \qquad = \frac{1}{2}\parallel y{(3)}-a{(3)}\parallel \ \qquad =\frac{1}{2}\left [(y{(3)}_1-a{(3)}_1)2+(y{(3)}_2-a{(3)}_1)2 \right ] \ \qquad =\frac{1}{2}\left {\left [y{(3)}_1-f(z{(3)}_1)\right]^2+\left [y{(3)}_2-f(z{(3)}2)\right]^2\right } \ \qquad =\frac{1}{2}\left {\left [y{(3)}_1-f(w{3}{11}a^{(2)}_1 + w{3}_{21}a{(2)}_2 + w{3}_{31}a{(2)}3 + b{(3)}_1)\right]2+\left [y{(3)}_2-f(w{3}{12}a^{(2)}_1 + w{3}_{22}a{(2)}_2 + w{3}_{32}a{(2)}_3 + b{(3)}_2)\right]2\right } $
由链式求导法则去分别对 w 11 ( 3 ) 、 w 21 ( 3 ) 、 w 31 ( 3 ) \ w^{(3)}_{11}、w^{(3)}_{21}、w^{(3)}_{31} w11(3)、w21(3)、w31(3)求偏导
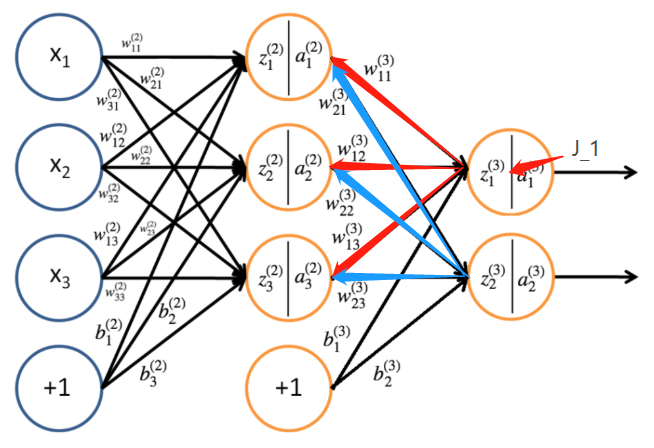
∂ J 3 ∂ w 11 ( 3 ) = ∂ J 3 ∂ a 1 ( 3 ) ∂ a 1 ( 3 ) ∂ z 1 ( 3 ) ∂ z 1 ( 3 ) ∂ w 11 ( 3 ) \ \frac{\partial J_3}{\partial w^{(3)}_{11}}=\frac{\partial J_{3}}{\partial a^{(3)}_1}\frac{\partial a^{(3)}_1}{\partial z^{(3)}_1}\frac{\partial z^{(3)}_1}{\partial w^{(3)}_{11}} ∂w11(3)∂J3=∂a1(3)∂J3∂z1(3)∂a1(3)∂w11(3)∂z1(3)
∂ J 3 ∂ w 21 ( 3 ) = ∂ J 3 ∂ a 1 ( 3 ) ∂ a 1 ( 3 ) ∂ z 1 ( 3 ) ∂ z 1 ( 3 ) ∂ w 21 ( 3 ) \ \frac{\partial J_3}{\partial w^{(3)}_{21}}=\frac{\partial J_{3}}{\partial a^{(3)}_1}\frac{\partial a^{(3)}_1}{\partial z^{(3)}_1}\frac{\partial z^{(3)}_1}{\partial w^{(3)}_{21}} ∂w21(3)∂J3=∂a1(3)∂J3∂z1(3)∂a1(3)∂w21(3)∂z1(3)
∂ J 3 ∂ w 31 ( 3 ) = ∂ J 3 ∂ a 1 ( 3 ) ∂ a 1 ( 3 ) ∂ z 1 ( 3 ) ∂ z 1 ( 3 ) ∂ w 31 ( 3 ) \ \frac{\partial J_3}{\partial w^{(3)}_{31}}=\frac{\partial J_{3}}{\partial a^{(3)}_1}\frac{\partial a^{(3)}_1}{\partial z^{(3)}_1}\frac{\partial z^{(3)}_1}{\partial w^{(3)}_{31}} ∂w31(3)∂J3=∂a1(3)∂J3∂z1(3)∂a1(3)∂w31(3)∂z1(3)
∂ J 3 ∂ w 12 ( 3 ) = ∂ J 3 ∂ a 2 ( 3 ) ∂ a 2 ( 3 ) ∂ z 2 ( 3 ) ∂ z 1 ( 3 ) ∂ w 12 ( 3 ) \ \frac{\partial J_3}{\partial w^{(3)}_{12}}=\frac{\partial J_{3}}{\partial a^{(3)}_2}\frac{\partial a^{(3)}_2}{\partial z^{(3)}_2}\frac{\partial z^{(3)}_1}{\partial w^{(3)}_{12}} ∂w12(3)∂J3=∂a2(3)∂J3∂z2(3)∂a2(3)∂w12(3)∂z1(3)
∂ J 3 ∂ w 22 ( 3 ) = ∂ J 3 ∂ a 2 ( 3 ) ∂ a 2 ( 3 ) ∂ z 2 ( 3 ) ∂ z 1 ( 3 ) ∂ w 22 ( 3 ) \ \frac{\partial J_3}{\partial w^{(3)}_{22}}=\frac{\partial J_{3}}{\partial a^{(3)}_2}\frac{\partial a^{(3)}_2}{\partial z^{(3)}_2}\frac{\partial z^{(3)}_1}{\partial w^{(3)}_{22}} ∂w22(3)∂J3=∂a2(3)∂J3∂z2(3)∂a2(3)∂w22(3)∂z1(3)
∂ J 3 ∂ w 32 ( 3 ) = ∂ J 3 ∂ a 2 ( 3 ) ∂ a 2 ( 3 ) ∂ z 2 ( 3 ) ∂ z 1 ( 3 ) ∂ w 32 ( 3 ) \ \frac{\partial J_3}{\partial w^{(3)}_{32}}=\frac{\partial J_{3}}{\partial a^{(3)}_2}\frac{\partial a^{(3)}_2}{\partial z^{(3)}_2}\frac{\partial z^{(3)}_1}{\partial w^{(3)}_{32}} ∂w32(3)∂J3=∂a2(3)∂J3∂z2(3)∂a2(3)∂w32(3)∂z1(3)
再拿 w 11 ( 3 ) \ w^{(3)}_{11} w11(3)为例,带入求偏导得:
∂ J 3 ∂ w 11 ( 3 ) = 1 2 ⋅ 2 ( y 1 ( 3 ) − a 1 ( 3 ) ) ( − ∂ a 1 ( 3 ) ∂ w 11 ( 3 ) ) = − ( y 1 ( 3 ) − a 1 ( 3 ) ) f ′ ( z 1 ( 3 ) ) ∂ z 1 ( 3 ) ∂ w 11 ( 3 ) = − ( y 1 ( 3 ) − a 1 ( 3 ) ) f ′ ( z 1 ( 3 ) ) a 1 ( 2 ) \ \frac{\partial J_3}{\partial w^{(3)}_{11}}=\frac{1}{2}\cdot 2(y^{(3)}_1-a^{(3)}_1)(-\frac{\partial a^{(3)}_1}{\partial w^{(3)}_{11}}) \\ \qquad \quad = -(y^{(3)}_1-a^{(3)}_1) f'(z^{(3)}_1)\frac{\partial z^{(3)}_1}{\partial w^{(3)}_{11}} \\ \qquad = -(y^{(3)}_1-a^{(3)}_1)f'(z^{(3)}_1)a^{(2)}_1 ∂w11(3)∂J3=21⋅2(y1(3)−a1(3))(−∂w11(3)∂a1(3))=−(y1(3)−a1(3))f′(z1(3))∂w11(3)∂z1(3)=−(y1(3)−a1(3))f′(z1(3))a1(2)
根据上面的公式,我们令:
δ i ( l ) = ∂ J ∂ z i ( l ) = ∂ J ∂ a i ( l ) ∂ a i ( l − 1 ) ∂ z i ( l ) = − ( y i ( l ) − a i ( l ) ) f ′ ( z i ( l ) ) \ \delta^{(l)}_i = \frac{\partial J}{\partial z^{(l)}_i}= \frac{\partial J}{\partial a^{(l)}_i}\frac{\partial a^{(l-1)}_i}{\partial z^{(l)}_i} = -(y^{(l)}_i-a^{(l)}_i)f'(z^{(l)}_i) δi(l)=∂zi(l)∂J=∂ai(l)∂J∂zi(l)∂ai(l−1)=−(yi(l)−ai(l))f′(zi(l))
所以:
∂ J ∂ w 11 ( 3 ) = δ 1 ( 3 ) a 1 ( 2 ) \ \frac{\partial J}{\partial w^{(3)}_{11}}=\delta^{(3)}_1a^{(2)}_1 ∂w11(3)∂J=δ1(3)a1(2)
∂ J ∂ w 21 ( 3 ) = δ 1 ( 3 ) a 2 ( 2 ) \ \frac{\partial J}{\partial w^{(3)}_{21}}=\delta^{(3)}_1a^{(2)}_2 ∂w21(3)∂J=δ1(3)a2(2)
∂ J ∂ w 31 ( 3 ) = δ 1 ( 3 ) a 3 ( 2 ) \ \frac{\partial J}{\partial w^{(3)}_{31}}=\delta^{(3)}_1a^{(2)}_3 ∂w31(3)∂J=δ1(3)a3(2)
∂ J ∂ w 12 ( 3 ) = δ 2 ( 3 ) a 1 ( 2 ) \ \frac{\partial J}{\partial w^{(3)}_{12}}=\delta^{(3)}_2a^{(2)}_1 ∂w12(3)∂J=δ2(3)a1(2)
∂ J ∂ w 22 ( 3 ) = δ 2 ( 3 ) a 2 ( 2 ) \ \frac{\partial J}{\partial w^{(3)}_{22}}=\delta^{(3)}_2a^{(2)}_2 ∂w22(3)∂J=δ2(3)a2(2)
∂ J ∂ w 32 ( 3 ) = δ 2 ( 3 ) a 3 ( 2 ) \ \frac{\partial J}{\partial w^{(3)}_{32}}=\delta^{(3)}_2a^{(2)}_3 ∂w32(3)∂J=δ2(3)a3(2)
所以,假设神经网络一共由 L \ L L层,那么对一般式而言:
δ i ( L ) = − ( y i ( L ) − a i ( L ) ) f ′ ( z i ( L ) ) \ \delta^{(L)}_i = -(y^{(L)}_i-a^{(L)}_i)f'(z^{(L)}_i) δi(L)=−(yi(L)−ai(L))f′(zi(L))
∂ J w i j ( L ) = δ i ( L ) a i ( L − 1 ) \ \frac{\partial J}{w^{(L)}_{ij}} = \delta^{(L)}_ia^{(L-1)}_i wij(L)∂J=δi(L)ai(L−1)
对向量/矩阵运算:
δ ( L ) = − ( y ( L ) − a ( L ) ) ⊙ f ′ ( z ( L ) ) \ \delta^{(L)} = -(y^{(L)}-a^{(L)})\odot f'(z^{(L)}) δ(L)=−(y(L)−a(L))⊙f′(z(L))
▽ W ( L ) J = δ ( L ) ( a ( L − 1 ) ) T \ \bigtriangledown_{W^{(L)}}J = \delta^{(L)}(a^{(L-1)})^T ▽W(L)J=δ(L)(a(L−1))T
再用这个式子进行权重的更新即可
隐藏层权重更新
隐藏层的权重更新也是使用链式法则求偏导数,只不过平时使用的都是向量而已:
对 w 11 ( 2 ) \ w^{(2)}_{11} w11(2)更新:
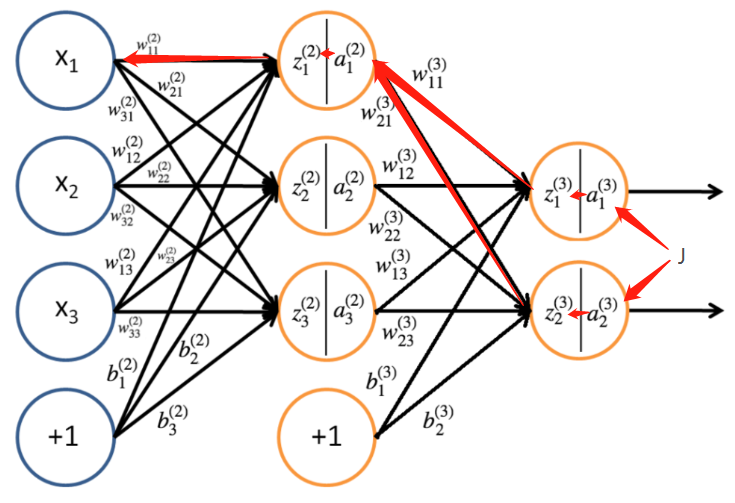
∂ J 3 ∂ w 11 ( 2 ) = ∂ J 3 ∂ a 1 ( 3 ) ∂ a 1 ( 3 ) ∂ z 1 ( 3 ) ∂ z 1 ( 3 ) ∂ a 1 ( 2 ) ∂ a 1 ( 2 ) ∂ z 1 ( 2 ) z 1 ( 2 ) w 11 ( 2 ) + ∂ J 3 ∂ a 2 ( 3 ) ∂ a 2 ( 3 ) ∂ z 2 ( 3 ) ∂ z 2 ( 3 ) ∂ a 1 ( 2 ) ∂ a 1 ( 2 ) ∂ z 1 ( 2 ) z 1 ( 2 ) w 11 ( 2 ) \ \frac{\partial J_3}{\partial w^{(2)}_{11}}=\frac{\partial J_{3}}{\partial a^{(3)}_1}\frac{\partial a^{(3)}_1}{\partial z^{(3)}_1}\frac{\partial z^{(3)}_1}{\partial a^{(2)}_{1}}\frac{\partial a^{(2)}_{1}}{\partial z^{(2)}_1}\frac{z^{(2)}_1}{w^{(2)}_{11}}+\frac{\partial J_{3}}{\partial a^{(3)}_2}\frac{\partial a^{(3)}_2}{\partial z^{(3)}_2}\frac{\partial z^{(3)}_2}{\partial a^{(2)}_{1}}\frac{\partial a^{(2)}_{1}}{\partial z^{(2)}_1}\frac{z^{(2)}_1}{w^{(2)}_{11}} ∂w11(2)∂J3=∂a1(3)∂J3∂z1(3)∂a1(3)∂a1(2)∂z1(3)∂z1(2)∂a1(2)w11(2)z1(2)+∂a2(3)∂J3∂z2(3)∂a2(3)∂a1(2)∂z2(3)∂z1(2)∂a1(2)w11(2)z1(2)
再结合
其他隐藏层权重更新同理,在这里不再过多赘述
接着使用刚刚我们定义的 δ i ( l ) \ \delta^{(l)}_i δi(l)推导公式
∂ J ∂ w i j ( l ) = ∂ J ∂ z i ( l ) = δ i ( l ) ∂ z i ( l ) w i j ( l ) = δ i ( l ) a j ( l − 1 ) \ \frac{\partial J}{\partial w^{(l)}_{ij}}=\frac{\partial J}{\partial z^{(l)}_i}=\delta^{(l)}_i\frac{\partial z^{(l)}_i}{w^{(l)}_{ij}}=\delta^{(l)}_ia^{(l-1)}_j ∂wij(l)∂J=∂zi(l)∂J=δi(l)wij(l)∂zi(l)=δi(l)aj(l−1)
当在隐藏层时,又链式法则和函数和求导公式就有:
∂ J ∂ z i ( l ) = ∂ J ∂ z 1 ( l − 1 ) ∂ z 1 ( l − 1 ) ∂ z ( i ) + ∂ J ∂ z 2 ( l − 1 ) ∂ z 2 ( l − 1 ) ∂ z ( i ) + ⋅ ⋅ ⋅ + ∂ J ∂ z n l + 1 ( l − 1 ) ∂ z n l + 1 ( l − 1 ) ∂ z ( i ) = ∑ j = 1 n l + 1 ∂ J ∂ z j ( l + 1 ) ∂ z j l + 1 ∂ z i l \ \frac{\partial J}{\partial z^{(l)}_i} = \frac{\partial J}{\partial z^{(l-1)}_1}\frac{\partial z^{(l-1)}_1}{\partial z^{(i)}}+\frac{\partial J}{\partial z^{(l-1)}_2}\frac{\partial z^{(l-1)}_2}{\partial z^{(i)}}+···+\frac{\partial J}{\partial z^{(l-1)}_{n_l+1}}\frac{\partial z^{(l-1)}_{n_l+1}}{\partial z^{(i)}}=\sum^{n_l+1}_{j=1}\frac{\partial J}{\partial z^{(l+1)}_j}\frac{\partial z^{l+1}_j}{\partial z^{l}_i} ∂zi(l)∂J=∂z1(l−1)∂J∂z(i)∂z1(l−1)+∂z2(l−1)∂J∂z(i)∂z2(l−1)+⋅⋅⋅+∂znl+1(l−1)∂J∂z(i)∂znl+1(l−1)=j=1∑nl+1∂zj(l+1)∂J∂zil∂zjl+1
所以
$$\ \delta^{(l)}_i = \frac{\partial J}{\partial z^{(l)}_i}=\sum^{n_l+1}_{j=1}\frac{\partial J}{\partial z^{(l+1)}_j}\frac{\partial z^{l+1}_j}{\partial z^{l}_i}=\sum^{n_l+1}_{j=1}\delta^{(l+1)}_j\frac{\partial z^{l+1}_j}{\partial z^{l}_i} $$又因为
z j ( l + 1 ) = ∑ i = 1 n l w j i ( l + 1 ) a i ( l ) + b j ( l + 1 ) = ∑ i = 1 n l w j i ( l + 1 ) f ( z i ( l ) ) + b j ( l + 1 ) \ z^{(l+1)}_j=\sum^{n_l}_{i=1}w^{(l+1)}_{ji}a^{(l)}_i+b^{(l+1)}_j = \sum^{n_l}_{i=1}w^{(l+1)}_{ji}f(z^{(l)}_i)+b^{(l+1)}_j zj(l+1)=i=1∑nlwji(l+1)ai(l)+bj(l+1)=i=1∑nlwji(l+1)f(zi(l))+bj(l+1)
所以有:
∂ z j ( l + 1 ) ∂ z i ( l ) = ∂ z j ( l + 1 ) ∂ a i ( l ) ∂ a i ( l ) ∂ z j ( l ) = w j i ( l + 1 ) f z i ( l ) \ \frac{\partial z^{(l+1)}_j}{\partial z^{(l)}_i}= \frac{\partial z^{(l+1)}_j}{\partial a^{(l)}_i}\frac{\partial a^{(l)}_i}{\partial z^{(l)}_j}=w^{(l+1)}_{ji}f{z^{(l)}_i} ∂zi(l)∂zj(l+1)=∂ai(l)∂zj(l+1)∂zj(l)∂ai(l)=wji(l+1)fzi(l)
再带入前面的 δ i ( l ) \ \delta^{(l)}_i δi(l):
$$\ \delta^{(l)}_i = f'(z^{(l)}_i)\sum^{n_l+1}_{j=1}\delta^{(l+1)}_{j}w^{(l+1)}_{ji} $$ 对向量/矩阵运算: $$\ \delta^{(l)}_i = f'(z^{(l)}_i)\odot (W^{(l+1)})^T\delta^{(l+1)} $$输出层偏置更新
偏置的更新其实和权重更新是一样的
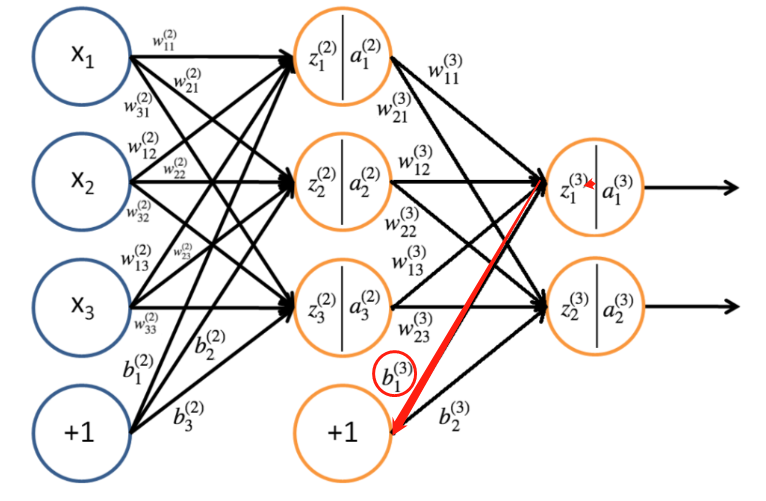
输出层的偏置比较好算
∂ J ∂ b 1 ( 3 ) = ∂ J ∂ a 1 ( 3 ) ∂ a 1 ( 3 ) ∂ z 1 ( 3 ) z 1 ( 3 ) b 1 ( 3 ) \ \frac{\partial J}{\partial b^{(3)}_1} = \frac{\partial J}{\partial a^{(3)}_1}\frac{\partial a^{(3)}_1}{\partial z^{(3)}_1}\frac{z^{(3)}_1}{b^{(3)}_1} ∂b1(3)∂J=∂a1(3)∂J∂z1(3)∂a1(3)b1(3)z1(3)
∂ J ∂ b 2 ( 3 ) = ∂ J ∂ a 2 ( 3 ) ∂ a 2 ( 3 ) ∂ z 2 ( 3 ) z 2 ( 3 ) b 2 ( 3 ) \ \frac{\partial J}{\partial b^{(3)}_2} = \frac{\partial J}{\partial a^{(3)}_2}\frac{\partial a^{(3)}_2}{\partial z^{(3)}_2}\frac{z^{(3)}_2}{b^{(3)}_2} ∂b2(3)∂J=∂a2(3)∂J∂z2(3)∂a2(3)b2(3)z2(3)
再结合
隐藏层偏执更新
隐藏层偏置更新和权重更新也是一个道理
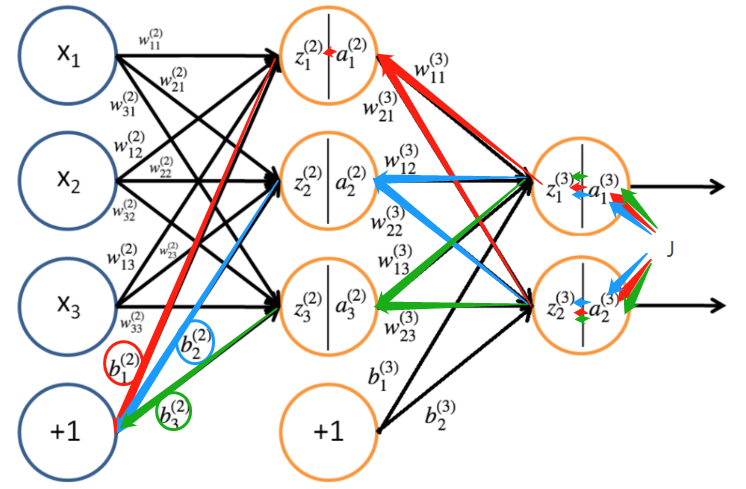
∂ J ∂ b 1 ( 2 ) = ∂ J ∂ a 1 ( 3 ) ∂ a 1 ( 3 ) ∂ z 1 ( 3 ) z 1 ( 3 ) a 1 ( 2 ) a 1 ( 2 ) z 1 ( 2 ) z 1 ( 2 ) b 1 ( 2 ) + ∂ J ∂ a 2 ( 3 ) ∂ a 2 ( 3 ) ∂ z 2 ( 3 ) z 2 ( 3 ) a 1 ( 2 ) a 1 ( 2 ) z 1 ( 2 ) z 1 ( 2 ) b 1 ( 2 ) \ \frac{\partial J}{\partial b^{(2)}_1} = \frac{\partial J}{\partial a^{(3)}_1}\frac{\partial a^{(3)}_1}{\partial z^{(3)}_1}\frac{z^{(3)}_1}{a^{(2)}_1}\frac{a^{(2)}_1}{z^{(2)}_1}\frac{z^{(2)}_1}{b^{(2)}_1}+\frac{\partial J}{\partial a^{(3)}_2}\frac{\partial a^{(3)}_2}{\partial z^{(3)}_2}\frac{z^{(3)}_2}{a^{(2)}_1}\frac{a^{(2)}_1}{z^{(2)}_1}\frac{z^{(2)}_1}{b^{(2)}_1} ∂b1(2)∂J=∂a1(3)∂J∂z1(3)∂a1(3)a1(2)z1(3)z1(2)a1(2)b1(2)z1(2)+∂a2(3)∂J∂z2(3)∂a2(3)a1(2)z2(3)z1(2)a1(2)b1(2)z1(2)
∂ J ∂ b 2 ( 2 ) = ∂ J ∂ a 1 ( 3 ) ∂ a 1 ( 3 ) ∂ z 1 ( 3 ) z 1 ( 3 ) a 2 ( 2 ) a 2 ( 2 ) z 2 ( 2 ) z 2 ( 2 ) b 2 ( 2 ) + ∂ J ∂ a 2 ( 3 ) ∂ a 2 ( 3 ) ∂ z 2 ( 3 ) z 2 ( 3 ) a 2 ( 2 ) a 2 ( 2 ) z 2 ( 2 ) z 2 ( 2 ) b 2 ( 2 ) \ \frac{\partial J}{\partial b^{(2)}_2} = \frac{\partial J}{\partial a^{(3)}_1}\frac{\partial a^{(3)}_1}{\partial z^{(3)}_1}\frac{z^{(3)}_1}{a^{(2)}_2}\frac{a^{(2)}_2}{z^{(2)}_2}\frac{z^{(2)}_2}{b^{(2)}_2}+\frac{\partial J}{\partial a^{(3)}_2}\frac{\partial a^{(3)}_2}{\partial z^{(3)}_2}\frac{z^{(3)}_2}{a^{(2)}_2}\frac{a^{(2)}_2}{z^{(2)}_2}\frac{z^{(2)}_2}{b^{(2)}_2} ∂b2(2)∂J=∂a1(3)∂J∂z1(3)∂a1(3)a2(2)z1(3)z2(2)a2(2)b2(2)z2(2)+∂a2(3)∂J∂z2(3)∂a2(3)a2(2)z2(3)z2(2)a2(2)b2(2)z2(2)
∂ J ∂ b 3 ( 2 ) = ∂ J ∂ a 1 ( 3 ) ∂ a 1 ( 3 ) ∂ z 1 ( 3 ) z 1 ( 3 ) a 3 ( 2 ) a 3 ( 2 ) z 3 ( 2 ) z 3 ( 2 ) b 3 ( 2 ) + ∂ J ∂ a 2 ( 3 ) ∂ a 2 ( 3 ) ∂ z 2 ( 3 ) z 2 ( 3 ) a 3 ( 2 ) a 3 ( 2 ) z 3 ( 2 ) z 3 ( 2 ) b 3 ( 2 ) \ \frac{\partial J}{\partial b^{(2)}_3} = \frac{\partial J}{\partial a^{(3)}_1}\frac{\partial a^{(3)}_1}{\partial z^{(3)}_1}\frac{z^{(3)}_1}{a^{(2)}_3}\frac{a^{(2)}_3}{z^{(2)}_3}\frac{z^{(2)}_3}{b^{(2)}_3}+\frac{\partial J}{\partial a^{(3)}_2}\frac{\partial a^{(3)}_2}{\partial z^{(3)}_2}\frac{z^{(3)}_2}{a^{(2)}_3}\frac{a^{(2)}_3}{z^{(2)}_3}\frac{z^{(2)}_3}{b^{(2)}_3} ∂b3(2)∂J=∂a1(3)∂J∂z1(3)∂a1(3)a3(2)z1(3)z3(2)a3(2)b3(2)z3(2)+∂a2(3)∂J∂z2(3)∂a2(3)a3(2)z2(3)z3(2)a3(2)b3(2)z3(2)
再根据对权重的推论,同理可得:
$$\ \delta^{(l)}_i = \frac{\partial J}{\partial b^{(l)}_i}=\frac{\partial J}{\partial z^{(l)}_i}\frac{\partial z^{(l)}_i}{b^{(l)}_i} $$ 对向量/矩阵运算: $$\ \delta^{l}=\bigtriangledown_b^{(l)}J $$再结合: