版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/zhq9695/article/details/82814197
目录
学习完吴恩达老师机器学习课程的逻辑回归，简单的做个笔记。文中部分描述属于个人消化后的理解，仅供参考。
0. 前言
逻辑回归（Logistic Regression），是一种用于二分类（binary classification）的算法。我们可假设：
--- 代表二分类中的正类
--- 代表二分类中的反类
1. 假设函数（Hypothesis）
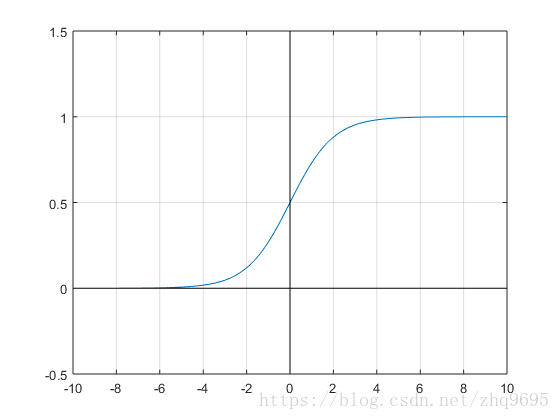
首先给出一个函数，Sigmoid 函数，，它的函数图像如下所示：
我们知道，在线性回归算法中，假设函数被定义为 ，此时假设函数的取值范围可以为
。在二分类中，输出
的取值只能为
或者
，在
之外包裹一层 Sigmoid 函数，使之取值范围属于
，所以给出如下定义：
例如 ，表示有
的概率
，表示输入为
时，
的概率。
2. 决策边界（Decision Boundary）
根据以上假设函数表示概率，我们可以推得：
令 ，则
为决策边界。如果用图像表示，如下例子：
3. 代价函数（Cost Funciton）
在线性回归中，我们给出定义 ，由于它是一个凸函数，所以可用梯度下降直接求解，局部最小值即全局最小值。
但在逻辑回归中， 是一个复杂的非线性函数，属于非凸函数，直接使用梯度下降会陷入局部最小值中。
根据极大似然估计（Maximum likelihood Estimate），可对代价函数作如下修改：
当 时，我们对
作图如下。易知当
（可判定
）时，代价是接近无穷大的（因为此时判错），反之亦然。
我们亦可将代价函数写成如下形式：
此时的代价函数是凸函数，可用梯度下降法求全局最优解。
4. 梯度下降（Gradient Descent）
与线性回归一致，梯度下降仍然采用如下公式：
5. 逻辑回归实现多分类
多分类（multi-classification）是指分类的结果不只两类，而是有多个类别。
逻辑回归本质上是一种二分类的算法，但是可以通过搭建多个二分类器的思想，实现多分类。
- 针对类别
，设
- 针对类别
，设
- 针对类别
，设
- ........
由于 ，即求
时的
。
6. 其他求解参数的方法
除了梯度下降外，还有以下求解方法：
- 共轭梯度法（Conjugate Gradient）
- BFGS
- L-BFGS
在这些方法中，相比梯度下降，有以下优点和缺点：
- 不需要主观的选择学习率
，算法中的内循环会自动调节
- 速度更快
- 算法更复杂