逻辑回归的模型
希望:![]()
我们详细说明一下机器学习(6)中的相关概念
1 假说表示
由于逻辑回归要求我们的输出值在 0 和 1 之间,因此我们需要有一个满足0≤hθx≤1![]() 的假设函数:
的假设函数:
![]()
其中,x ![]() 为特征向量,g
为特征向量,g![]() 为逻辑函数,也叫做S形函数(Sigmoid Function)或者叫做逻辑函数(Logistic Fuction),它具体为:
为逻辑函数,也叫做S形函数(Sigmoid Function)或者叫做逻辑函数(Logistic Fuction),它具体为:
![]()
逻辑函数在图像上具体是这样子的:
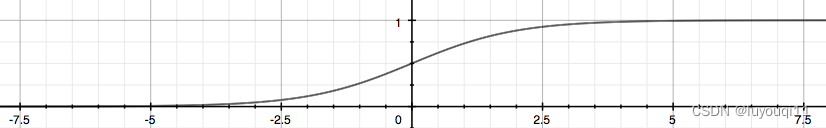
不难看出逻辑函数左侧无限趋近 0,右侧无限趋近 1,这正符合我们所需要的模型的输出值介于 0 和 1 之间。
讲上面两个式子结合一下,我们的假设函数也可以写作:
![]()
![]() 的作用是,根据设定的参数,输入给定的变量,计算输出变量的值为 1 的可能性(Estimated Probablity),即 :
的作用是,根据设定的参数,输入给定的变量,计算输出变量的值为 1 的可能性(Estimated Probablity),即 :
![]()
由概率定义知:
![]()
因此:
![]()
假设![]() ,表示 y 属于正向类的可能性为 70%,所以 y=0 的概率为 30% 。
,表示 y 属于正向类的可能性为 70%,所以 y=0 的概率为 30% 。
2 决策界限(Decision Boundary)
可以更好地理解逻辑回归中的假设函数的作用。
![]()
逻辑函数在图像上具体是这样子的:
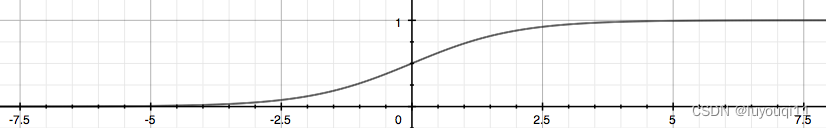
不难看出逻辑函数左侧无限趋近 0,右侧无限趋近 1,这正符合我们所需要的模型的输出值介于 0 和 1 之间。
如果我们预测:如果 ![]() 如果
如果![]() 即:
即:
- 当
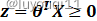 时,
时,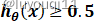 ,
, 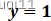 ;
; - 当
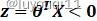 时,
时,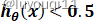 ,
,  ;
;
于是![]() 就成了决策边界。
就成了决策边界。
决策边界(Decision Boundary)由假设函数决定,理论上可以为任意曲线,也就是说根据模型计算得到的值再由决策边界进行决定最终属于正向类还是负向类。
例子:线性决策边界
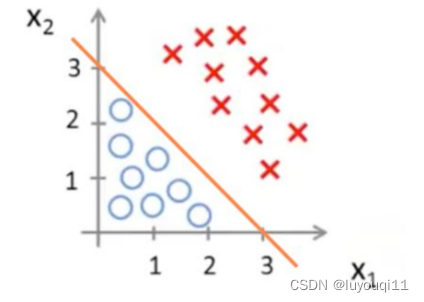
假设函数:![]()
逻辑函数:![]()
参数:![]() ,
,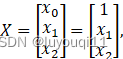
![]()
预测:当![]() 即
即![]() 时,模型预测
时,模型预测 ![]() 。
。
当![]() 即
即 ![]() 时,模型预测
时,模型预测![]() 。
。
决策边界:![]() ,将预测值为 1 和 0 的两个区域区分开来。
,将预测值为 1 和 0 的两个区域区分开来。
例子:非线性决策边界
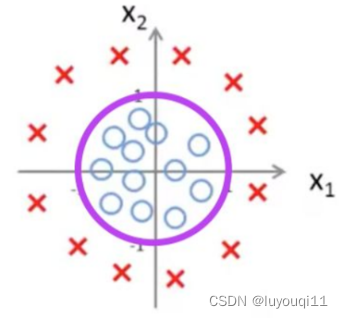
还有更加复杂的情况,如果数据像以上的图形:
则需要曲线才能将两个类区分开来,就需要用到二次方,如:
假设函数:![]()
逻辑函数:![]()
参数假设为:![]() ,
,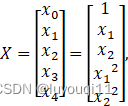 ,
,![]()
预测:当![]() 即
即![]() 时,模型预测
时,模型预测![]() 。
。
当![]() 即
即 ![]() 时,模型预测
时,模型预测![]() 。。
。。
决策边界:![]() ,则曲线正好是以原点为圆心,1 为半径的圆。将预测值为 1 和 0 的两个区域区分开来。
,则曲线正好是以原点为圆心,1 为半径的圆。将预测值为 1 和 0 的两个区域区分开来。
我们可以用任意复杂的曲线作为分布复杂的数据的决策边界。
3 代价函数(Cost Fuction)
训练集(Training Set):![]()
m个样本: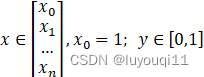
假设函数:![]()
决策边界:![]()
问题:如何选择参数θ呢?
这就涉及到了逻辑回归的拟合问题。
定义
由线性回归的代价函数:
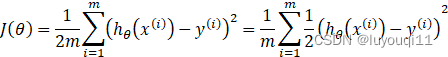
若我们定义:
![]()
则有:

称![]() 为逻辑回归的单样本代价函数
为逻辑回归的单样本代价函数
称 ![]() 为逻辑回归的代价函数,
为逻辑回归的代价函数,
我们将![]() 代入代价函数,则有:
代入代价函数,则有:
![]()
该函数是个非凸函数,这会导致在梯度下降时没有全局最优解。于是我们必须另外选择一个代价函数。如:

这个函数看起来很复杂,但画出图形如下:
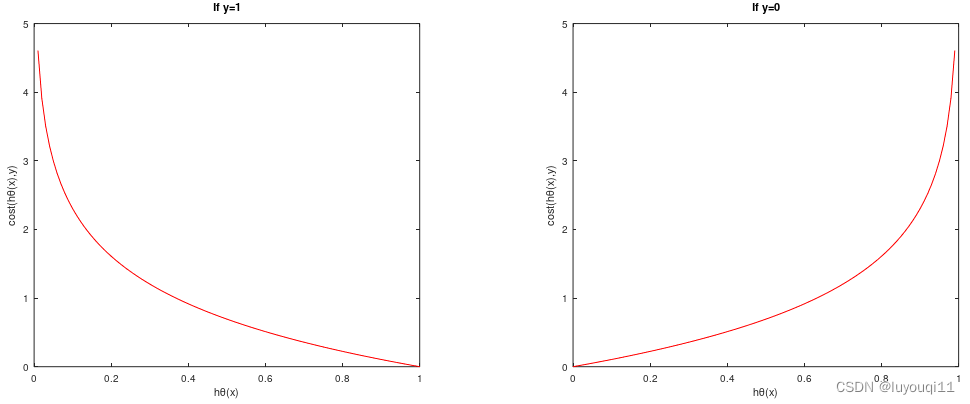
通过上面图形,我们知道:
预测:如果 ![]() ,预测y=1,此时Cost=0 。(正常预测)
,预测y=1,此时Cost=0 。(正常预测)
如果![]() ,预测y=1,此时Cost=0.8。(正常预测)
,预测y=1,此时Cost=0.8。(正常预测)
如果![]() ,预测y=1,此时Cost→∞ 。(极不正常预测)
,预测y=1,此时Cost→∞ 。(极不正常预测)
反之:如果 ![]() ,预测y=0,此时Cost→∞ 。(极不正常预测)
,预测y=0,此时Cost→∞ 。(极不正常预测)
如果![]() ,预测y=0,此时Cost=1 。(可疑预测,因为Cost比预测y=1大)
,预测y=0,此时Cost=1 。(可疑预测,因为Cost比预测y=1大)
如果 ![]() ,预测y=0,此时Cost=0 。(正常预测)
,预测y=0,此时Cost=0 。(正常预测)
以上图形,用Octave绘制的代码如下:
clear;clc;close;
x=[0:0.01:1];
y1=-log(x);
% 绘制第一个子图
subplot(1,2,1);
plot(x,y1,'r');
title('If y=1');x
label('hθ(x)');ylabel('cost(hθ(x),y)');
% 绘制第二个子图
y0=-log(1-x);
subplot(1,2,2);
plot(x,y0,'r');
title('If y=0');
xlabel('hθ(x)');
ylabel('cost(hθ(x),y)');
简化代价函数与梯度下降
逻辑回归的代价函数:![]()
单样本代价函数: 
注意:在逻辑回归中,y只能取0或1。
简化代价函数
以上单样本代价函数是不连续的,我们将其合并为一个式子,这样我们可以更方便地写出单样本代价函数,且可以运用梯度下降。结果如下:
![]()
逻辑回归的简化代价函数

这个式子的来源于统计学中的极大似然法,这是一种快速寻找参数的方法。
梯度下降求参数θ
逻辑回归的代价函数:![]()
找到合适的参数θ:使得![]() 最小。
最小。
选择一个合适输入特征x,输出:![]() 即
即![]()
代价函数的偏导函数:![]()
梯度下降寻找合适的参数θ:重复迭代![]()
观察![]() ,我们会惊人地发现形式上和以前的线性回归是一样的。
,我们会惊人地发现形式上和以前的线性回归是一样的。
但是由于逻辑回归中假设函数和线性回归中的假设函数是不一样的:
- 在线性回归中
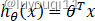 ,
, - 逻辑回归中

所以梯度下降的算法是完全不一样的。但是控制逻辑是一样的。
计算代价函数的高级优化
在梯度下降算法中,核心是计算![]() 和
和![]() ,选择合适的步长α,重复迭代
,选择合适的步长α,重复迭代
![]()
使得![]() 极小。
极小。
为了提高逻辑回归的效率,可以使用下面一些高级优化算法可以更快地求偏导数。
- 梯度下降(Gradient descent)
- 共轭梯度(Conjugate gradient)
- BFGS
- L-BFGS
以上三种算法的详细介绍已经超出了本书的内容,不详解。但这三种算法有共同的特点:
优点:
不需要自己手动选择学习速率,可智能选择合适的学习速率
比梯度下降法收敛的更快
缺点
比梯度下降法更复杂。
通常,我们不需要编写这些算法的代码,除非你是数值计算专家。我们一般是调用别人的软件库。Octave中就有这样的库,我们直接调用即可。需要注意的一点,如果你是使用其他高级语言如C++、Java,你可能需要多是几个不同的库,才能找到合适的算法。因为同一算法不同人编写的效率是不一样的,而这些算法的效率在数据量很大的情况下表现得差异特别明显。