1.介绍:
我们如何去衡量y,y`的接近程度?
在这里我们介绍一下一种衡量方式交叉熵(Cross-Entropy),然后说明一下为什么这种方式适用于分类问题。
2.熵(Entropy):
熵的概念来自物理中的热力学,表示热力学系统中的无序程度,我们说的熵是信息论中的熵,表示对不确定性的测量,熵越高,能传输的信息越多,熵越少,传输的信息越少。
也就是我们现在有了观测到的概率分布y,y_i = P(X=x_i)。我们要使用平均最小的bit,所以我们应该为x_i 分配log(1/y_i) 个比特。对所有的x_i 我们都有一个对应的最小需要分配的bit长度,那么我们对这个log(1/y_i)求期望也就得到了X的熵的定义了:
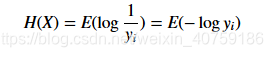
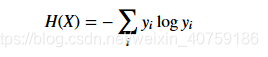
3.交叉熵(Cross-Entropy):
假如说我们用这个分布来作为我们来对事件编码的一个工具,熵就衡量了我们用这个正确的分布y来对事件编码所能用的最小的bit 长度,我们不能用更短的bit来编码这些事件或者符号了。
相对的,交叉熵是我们要对y这个分布去编码,但是我们用了一些模型估计分布y`。这里的话通过y`这个分布我们得到的关于x_i的最小编码长度就变成了log(1/y`_i),但是呢,我们的期望仍是关于真是分布y的。所以交叉熵的定义就变成了:
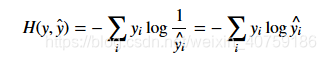
交叉熵是大于等于熵的,因为我们使用了错误的分布y`会带来更多的bit使用。当y和y`相等的时候,交叉熵就等于熵了。
4.KL 松散度(KL Divergence):
KL松散度和交叉熵的区别比较小,KL松散度又叫做相对熵,从定义很好看出区别:
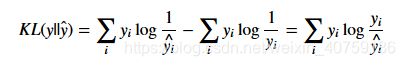
这个意思就是说我们要编码一个服从y分布的随机变量,假设我们使用了一些数据估计出来这个随机变量的分布是y`,那么我们需要用比真实的最小bit多多少来编码这个随机变量。这个值是大于等于0的,并且当,y和y`相等的时候才为0。注意这里对交叉熵求最小和对KL松散度求最小是一样的。也就是我们要调整参数使得交叉熵和熵更接近,KL松散度越接近0,也就是y`越接近y。
5.预测:
通过上面的描述和介绍,我们应该很高兴使用交叉熵来比较两个分布y,y`之间的不同,然后我们可以用所有训练数据的交叉熵的和来作为我们的损失,假如用n来表示我们训练数据的数量,则损失loss为:
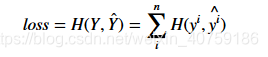
来对这个函数求最小值我们就可以求到最好的参数来使得y和y`最接近。
6.似然(Likelihood):
我们来看看另一种关于两个分布之间差异的测量标准–似然,这种标准更加直接,似然越大说明两个分布越接近,在分类问题中,我们会选择那些多数时候预测对了的模型。因为我们总是假设所有的数据点都是独立同分布的,对于所有数据的似然就可以定义为所有单个数据点的似然的乘积:
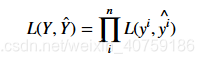
对于第n个数据他的似然怎么算呢?其实很简单,就是简单的y*y,来看一下我们最初的那个例子y={苹果:1,梨子:0},y`={苹果:0.4,梨子:0.6},所以似然就等于:
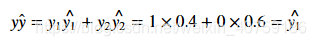
所以这里我们是不是可以考虑一下使用极大似然估计法来求最优参数呢?也就是求似然函数的极大值点。我们来对这个似然函数动一点点手脚。
我们知道对数函数使连续单调函数,我们要求似然函数的极大值等同于我们要求对数似然函数的极大值,然后我们取一个负,就等同于求负对数似然函数的极小值:
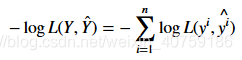
这样,我们就可以把似然函数中的累积连乘变成累加了。而且我们知道我们的观测结果y中两个元素必有一个元素是1,另一个元素是0.则对数似然函数为:

然后我们看看所有的数据的负对数似然:
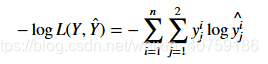
看着有没有一点眼熟?这就是我们上面的所有数据的交叉熵:
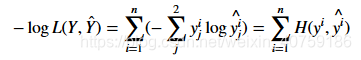
7.总结:
当我们做一个分类模型的时候,我们需要一种方法去衡量真实概率分布y和预测概率分布y`之间的差异,然后在训练过程中调整参数来减小这个差异。在这篇文章中我们可以看到交叉熵是一种不错的可行的选择,通过上面的这些等式可以看到,我们求交叉熵的极小值也就等同于我们求负对数似然的极小值。