EM Algorithm 从直观到数学理解

版权声明：转载需征求同意 https://blog.csdn.net/weixin_41483813/article/details/82352284

0x00 引言

EM算法是什么？什么是E（Epectation）？什么是M（Maximization）？什么又是公式里面出现的Q函数？这些公式都是怎么推导的？Nature抛硬币的那个图怎么就看不懂嘞？为什么看了那么多文章之后还是不懂？公式的符号怎么又不一样呢？谁谁还说有九层塔？Emmm…interesting

下面，让我们走进科学。

0x10 直观理解

现在有一个随机变量数据集$\mathbf{D}$，假设我们知道这个随机变量$\mathbf{X}$服从某种分布(一般是高斯正规分布），我们的目的是想知道这个分布的参数$\mathbf{\theta}$，可是随机变量$\mathbf{X}$里面包含不可知的参数（也就是隐变量$\mathbf{z}$）的时候，EM算法是在一边猜隐变量$\mathbf{z}$一边更新$\mathbf{\theta}$：

1. 先蒙一下目标参数$\mathbf{\theta}^{old}$
2. E步：利用测算的目标参数$\mathbf{\theta}^{old}$和数据集$\mathbf{D}$猜隐变量$\mathbf{z}$的分布
3. M步：利用上一步猜出来的隐变量$\mathbf{z}$反思更新目标参数$\mathbf{\theta}^{new}$
4. 重复上面两步直到目标参数$\mathbf{\theta}$收缩为止

再压缩成人话的话，数据集$\mathbf{D}$是以$\mathbf{z}$为比例而测出来的$\mathbf{X}$，先用$\mathbf{\theta}$蒙一个$\mathbf{z}$，然后用$\mathbf{z}$再算一个$\mathbf{\theta}$，如此反复。

0x20 抛硬币的例子

来源：Do, C. B., & Batzoglou, S. (2008). What is the expectation maximization algorithm? Nature Biotechnology, 26(8), 897–899. https://doi.org/10.1038/nbt1406

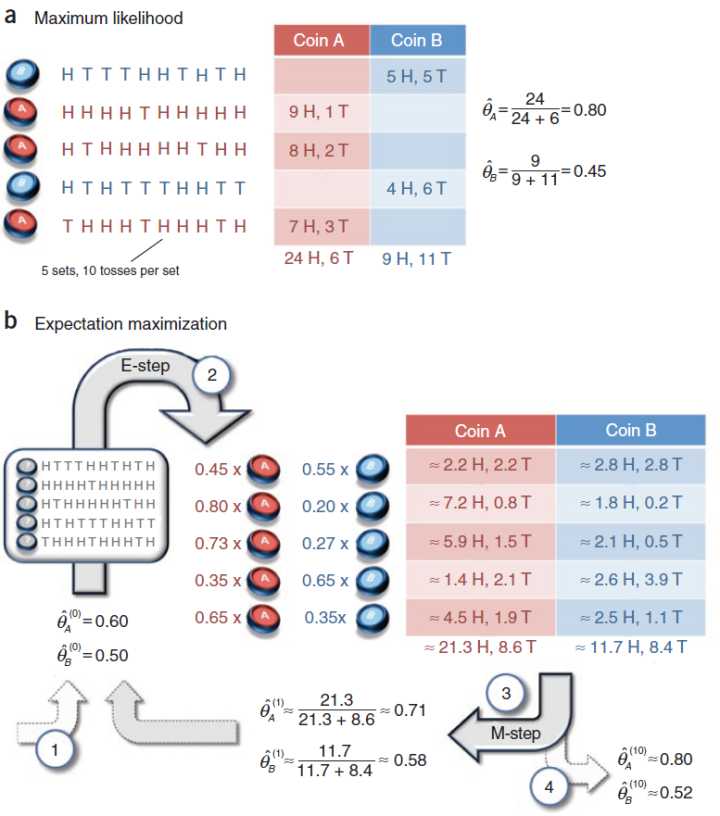
上面这篇著名的EM入门论文里面有一张很好的图例，利用抛硬币来说明EM，可是对于某些初学者来讲缺乏解读可能还是有点难理解思路。

下面尝试拆解一下分步骤解读

0x21 问题定义

已知：

• 手上有两种不同的硬币，分别称为A和B

实验：

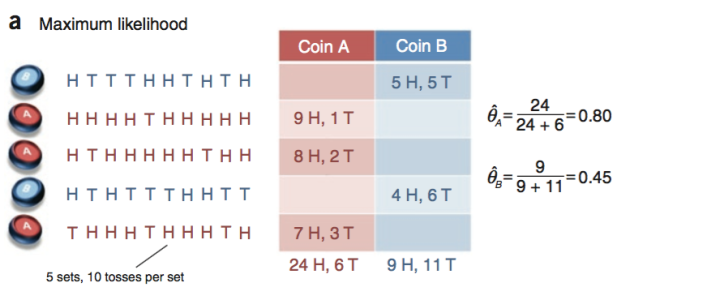
• 随机抛硬币十次为一组，记录正面朝上（H）和反面朝上（T）的数据
• 换硬币重复试验

问题：

• 分别求这两个硬币正面朝上的概率$\theta_{A}$和$\theta_{B}$

0x22 完全信息 vs 包含隐函数的不完全信息

上图的实验过程中如果记录了当时抛的是A或者B哪种硬币，统计推断的时候知道了每一组是属于哪一种硬币的情况下那当然很好算，这种情况叫完全信息。

假如实验中根本不知道抛的时候究竟是哪一种硬币，或者就不告诉你的话，我们就没办法直接计算两种硬币正面朝上的概率了，这种情况叫不完全信息。

例如上图的数据是和完全信息的情况一样的，区别在于左边的标签是问号，不知道是什么硬币。

这个时候就用到了EM算法。

0x23 完全信息下的求解

每次抛硬币都是独立的，从二项分布的期望公式$E[\mathbf{X}]=np$可以推导出$p=\frac{E[\mathbf{X}]}{n}=\frac{n_{ head}}{n}$。

• 对于A来说，一共抛了三组共三十次，共24次向上6次向下，那么A硬币朝上的概率是$\hat \theta_{A}=\frac{24}{30}=0.8$。

• 对于B来说，一共抛了两组共二十次，共9次向上11次向下，那么B硬币朝上的概率是$\hat \theta_{B}=\frac{9}{30}=0.45$。

0x24 不完全信息下的初级EM求解

不完全信息情况呢？我们根本不知道每一组的结果是属于哪种硬币的，没办法用0x24的方法算。这个时候硬币是否属于A的隐变量$z_n$是未知的。

（硬币的情况来说正常用二分法，$z_n= \begin{cases} 1, if \ coin \ A \\ 0, if \ coin \ B \end{cases}$，不过下面使用$z_n$代表数据重新分割的时候属于A的比例。）

 
 
 

那怎么办？

想一下就发现，一组抛多次，不同硬币的抛出不同结果的概率是相当不同的。比如说：

• 一个$\theta=0.3$的硬币抛出4H6T的概率是$P(4H6T|\theta=0.3)=\binom{10}{4}0.3^4(1-0.3)^6=\binom{10}{4}0.0009529569$
• 而$\theta=0.4$的硬币抛出4H6T的概率是$P(4H6T|\theta=0.4)=\binom{10}{4}0.4^4(1-0.4)^6=\binom{10}{4}0.0011943936$

也就是说，倒过来说，看到4H6T的结果的时候，这个硬币本身朝上的概率更有可能是$\theta=0.4$而不是$\theta=0.3$。

（注意有些文章里面的概率函数式子的写法用到了分号，$P(\theta;X)$，意思这是个以X为输入以$\theta$为变量的函数。为了方便，本文不使用；符号。）

所以说，已知$\theta_{A}$和$\theta_{B}$的话，我们可以通过观察抛出来的结果来推测原来硬币究竟是属于A还是B的！（这个做法叫做最大似然估计）

可是我们现在不知道$\theta_{A}$和$\theta_{B}$怎么办呢？这不是要求解的参数吗？

面对这个蛋生鸡还是鸡生蛋的cul-de-sac（死胡同），我们的做法是：先蒙一个！然后再不停互相更新修改。

 
 
 

具体步骤

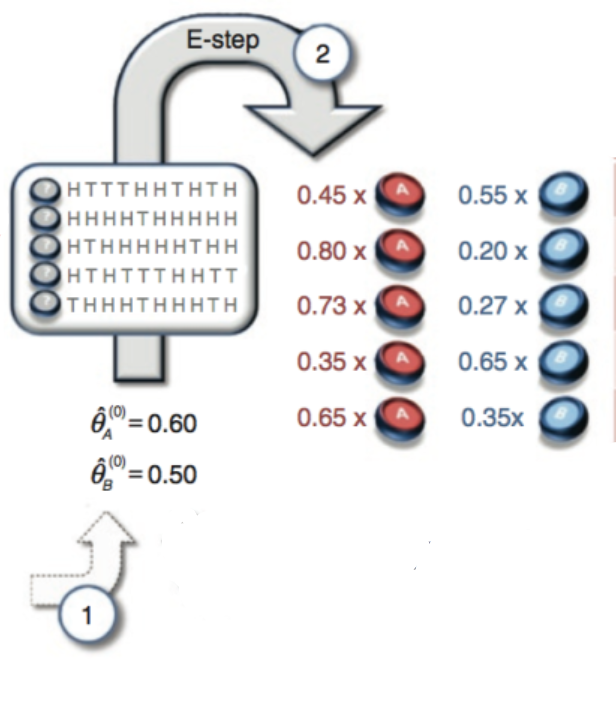
（1）先给$\theta_{A}$和$\theta_{B}$随便赋值。
比如$\theta_{A}^{(0)}=0.60$, $\theta_{B}^{(0)}=0.50$。

（2）然后算出

• A硬币抛出第一组的似然函数是$P(5H5T|\theta_{A}^{(0)}=0.6)=\binom{10}{5}0.6^5(1-0.6)^5=\binom{10}{5}0.0007962624$。
• B硬币抛出第一组的似然函数是$P(5H5T|\theta_{B}^{(0)}=0.5)=\binom{10}{5}0.5^5(1-0.5)^5=\binom{10}{5}0.0009765625$。

由此可以看到这组比较有可能是属于A。这个例子先按照比例来把第一组数据划分给A和B。

• 划分给A的比例是$z_1=\frac{P(5H5T|\theta_{A}^{(0)})}{P(5H5T|\theta_{A}^{(0)})+P(5H5T|\theta_{B}^{(0)})}\approx0.45$。
• 同理划分给B的比例是$1-z_1=\frac{P(5H5T|\theta_{B}^{(0)})}{P(5H5T|\theta_{A}^{(0)})+P(5H5T|\theta_{B}^{(0)})}\approx0.55$。

对其他组也进行推算，得到$z_2\approx0.80$，$z_3\approx0.73$，$z_4\approx0.35$，$z_5\approx0.65$。

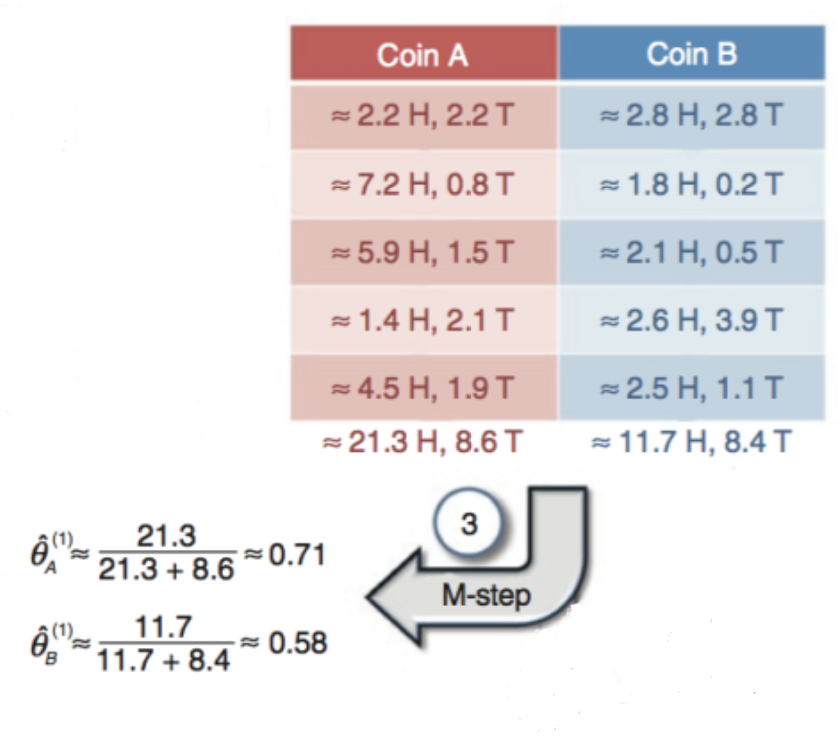
（3）接下来得到了新的划分后的数据，可以更新参数了

• 对于A来说，一共有21.3次向上8.6次向下，那么A硬币朝上的概率是$\hat \theta_{A}^{(1)}=\frac{21.3}{21.3+8.6}\approx0.71$。
• 对于B来说，一共有11.7次向上8.4次向下，那么B硬币朝上的概率是$\hat \theta_{B}^{(1)}=\frac{11.7}{11.7+8.4}\approx0.58$。

（4）重复步骤（2）和（3），直到收敛，可以算得第十次循环之后$\hat \theta_{A}^{(10)}\approx0.80$，$\hat \theta_{B}^{(10)}\approx0.52$。

可以看到这个结果也跟之前完全信息算出来的比较接近。

 
 
 

0x30 EM算法的公式推导

0x31 定义

• m个互相独立的样本组成的数据集$\mathbf{X}=(\mathbf{x}^{(1)},\mathbf{x}^{(2)},...\mathbf{x}^{(m)})$(这里每个$\mathbf{x}^{(k)}$对应硬币例子里面的一组共抛十次的数据，不知道每组属于哪种)
• 相对应的隐参数$\mathbf{z}=(z^{(1)},z^{(2)},...z^{(m)})$（每组数据属于哪种硬币的标记）
• 样本本身的模型参数$\mathbf{\theta}$（硬币例子就是$\mathbf{\theta}=(\theta_{A}, \theta_{B})$)

对应似然函数为

• 观察到$\mathbf{x}^{(k)}$的似然函数为$P(\mathbf{x}^{(k)}|\mathbf{\theta})$（例如硬币例子的$P(4H6T|\theta=0.3)$）
• 完全信息情况下的似然函数则是$P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})$（例如硬币例子的$P(4H6T,z=1|\theta_1=0.3,\theta_2=0.4)$。）
   
   
   

0x32 最大似然估计

那么为了求模型参数$\mathbf{\theta}$，将$\mathbf{\theta}$看成是参数，求解让各个样本的似然函数的乘积$L(\mathbf{\theta})$最大即可。

• 也就是$\mathbf{\theta}=\mathop{\arg\max}_{\mathbf{\theta}} L(\mathbf{\theta})= \mathop{\arg\max}_{\mathbf{\theta}} \prod_{k=1}^{m}P(\mathbf{x}^{(k)}|\mathbf{\theta})= \mathop{\arg\max}_{\mathbf{\theta}} \sum_{k=1}^{m} \log P(\mathbf{x}^{(k)}|\mathbf{\theta})$，让$L(\mathbf{\theta})$对$\mathbf{\theta}$求导为零容易算出$\mathbf{\theta}$
• 如果有隐函数的话则是$\mathbf{\theta},z=\mathop{\arg\max}_{\mathbf{\theta},z} L(\mathbf{\theta},z)= \mathop{\arg\max}_{\mathbf{\theta},z} \sum_{k=1}^{m} \log \sum_{z} P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})$，由于包含了$\log \sum_{z}P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})$这个时候求导的计算量就很繁杂了

解决思路是利用Jensen不等式$E[f(x)] \ge f(E(x))$,

将$\log \sum_{z}P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})$变成$\sum_{z} \log P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})$，即是下面的(1)到(2)，同时对P乘以了$\frac{q(z^{(k)})}{q(z^{(k)})}=1$。

因此，

$\begin{aligned} \sum_{k=1}^{m} \log \sum_{z} P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta}) & = \sum_{k=1}^{m} \log \sum_{z} q(z^{(k)}) \frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{q(z^{(k)})} \ \ \ (1) \\ & \ge \sum_{k=1}^{m} \sum_{z} q(z^{(k)}) \log \frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{q(z^{(k)})} \ \ (2) \\ & \to \sum_{k=1}^{m} \sum_{z} q(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta}^{old}) \log \frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{q(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta}^{old})} \ \ (3)\\ & = \sum_{k=1}^{m} \sum_{z} q(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta}^{old}) \log P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta}) \\ & \ \ \ - \sum_{k=1}^{m} \sum_{z} q(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta}^{old}) \log q(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta}^{old}) \ \ (4)\\ & = Q(\mathbf{\theta},\mathbf{\theta}^{old})+constant \ \ (5) \end{aligned}$

上面出来传说中的Q辅助函数，让Q最大化得出新的$\mathbf{\theta}$就是所谓的M步。从(2)到(3)步其实是E步。

所以EM算法就是上面推导公式的(3)(4)(5)之间不断循环直到收敛。

 
 

0x33 意义解读

E步来看,

（以下参考了人人都懂EM算法，略有修改）

(1)右边乘以了$\frac{q(z^{(k)})}{q(z^{(k)})}=1$，而引进的未知分布q满足$\sum_{z} q(z^{(k)})=1$

(2)里面的$\sum_{z} q(z^{(k)}) \log \frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{q(z^{(k)})}$其实是对$\log \frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{q(z^{(k)})}$求加权平均，也就是求它的数学期望（Expectation）：$E(\log \frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{q(z^{(k)})})$，这也是E步的名字来源。

为了让(2)能够取等号，也就是让$L(\mathbf{\theta},z)$取一个下限，Jensen不等式告诉我们上面的数学期望里面的变量需要是一个常数，即$\log \frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{q(z^{(k)})}=c$

去掉log之后有$P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})=cq(z^{(k)})$

累加后$\sum_{z}P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})=c\sum_{z}q(z^{(k)})=c$

所以即$q(z^{(k)})=\frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{c}=\frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{\sum_{z}P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}=\frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{P(\mathbf{x}^{(k)}|\mathbf{\theta})}=P(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta})$

q也就是已知$\mathbf{\theta}$和$\mathbf{x}^{(k)}$情况下求隐变量$\mathbf{z}^{(k)}$的分布，也就是隐变量的后验概率。然后我们才能继续算下面M步需要用到的$Q(\mathbf{\theta},\mathbf{\theta}^{old})$

$\mathbf{\theta}$不是未知数么？说得好，所以(3)里面代入了上次迭代算出的模型参数$\mathbf{\theta}^{old}$。

$Q(\mathbf{\theta},\mathbf{\theta}^{old})=E_{\mathbf{z}|\mathbf{X},\mathbf{\theta}^{old}}(\log L(\mathbf{X},\mathbf{Z}|\mathbf{\theta}))$

以上是E步。

M步来看，

最大化$Q(\mathbf{\theta},\mathbf{\theta}^{old})$更新$\mathbf{\theta}$。（(5)右边的constant可以忽略，不影响最大化似然函数的操作）

也就是$\mathbf{\theta}=\mathop{\arg\max}_{\mathbf{\theta}}Q(\mathbf{\theta},\mathbf{\theta}^{old})=\mathop{\arg\max}_{\mathbf{\theta}}\sum_{k=1}^{m} \sum_{z} q(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta}^{old}) \log P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})$

以上是M步。

另一个角度来看，

$\begin{aligned} \sum_{k=1}^{m} \log P(\mathbf{x}^{(k)}|\mathbf{\theta}) & = \sum_{k=1}^{m} \sum_{z} q(z^{(k)})\log \frac{P(\mathbf{x}^{(k)}|\mathbf{\theta})P(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta})}{P(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta})} \ \ \ \ (6)\\ & = \sum_{k=1}^{m} \sum_{z} q(z^{(k)})\log \frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{P(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta})} \ \ \ \ \ \ \ \ \ (7) \\ & = \sum_{k=1}^{m}\sum_{z} q(z^{(k)}) \{\log \frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{q(z^{(k)})}- \log\frac{P(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta})}{q(z^{(k)})}\} \ \ \ (8) \\ & = \sum_{k=1}^{m}\sum_{z} q(z^{(k)}) \log \frac{P(\mathbf{x}^{(k)},z^{(k)}|\mathbf{\theta})}{q(z^{(k)})}- \sum_{k=1}^{m}\sum_{z} q(z^{(k)}) \log \frac{P(z^{(k)}|\mathbf{x}^{(k)},\mathbf{\theta})}{q(z^{(k)})} \ \ \ (9) \\ & = L(\mathbf{\theta},z)+KL[q(\mathbf{z})|| P(\mathbf{z}|\mathbf{x},\mathbf{\theta})] \ \ \ \ \ \ \ \ \ \ \ \ \ (10)\end{aligned}$

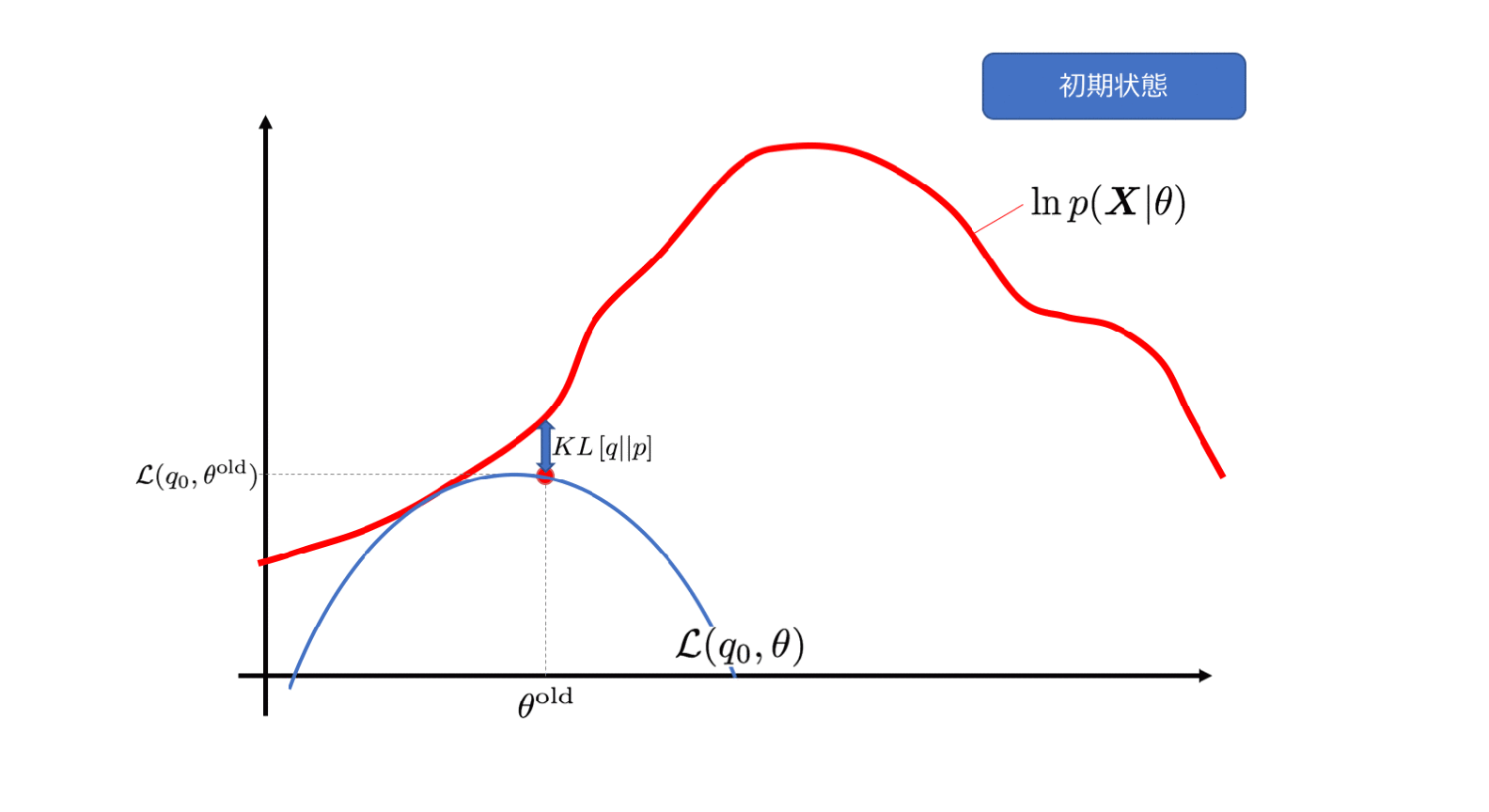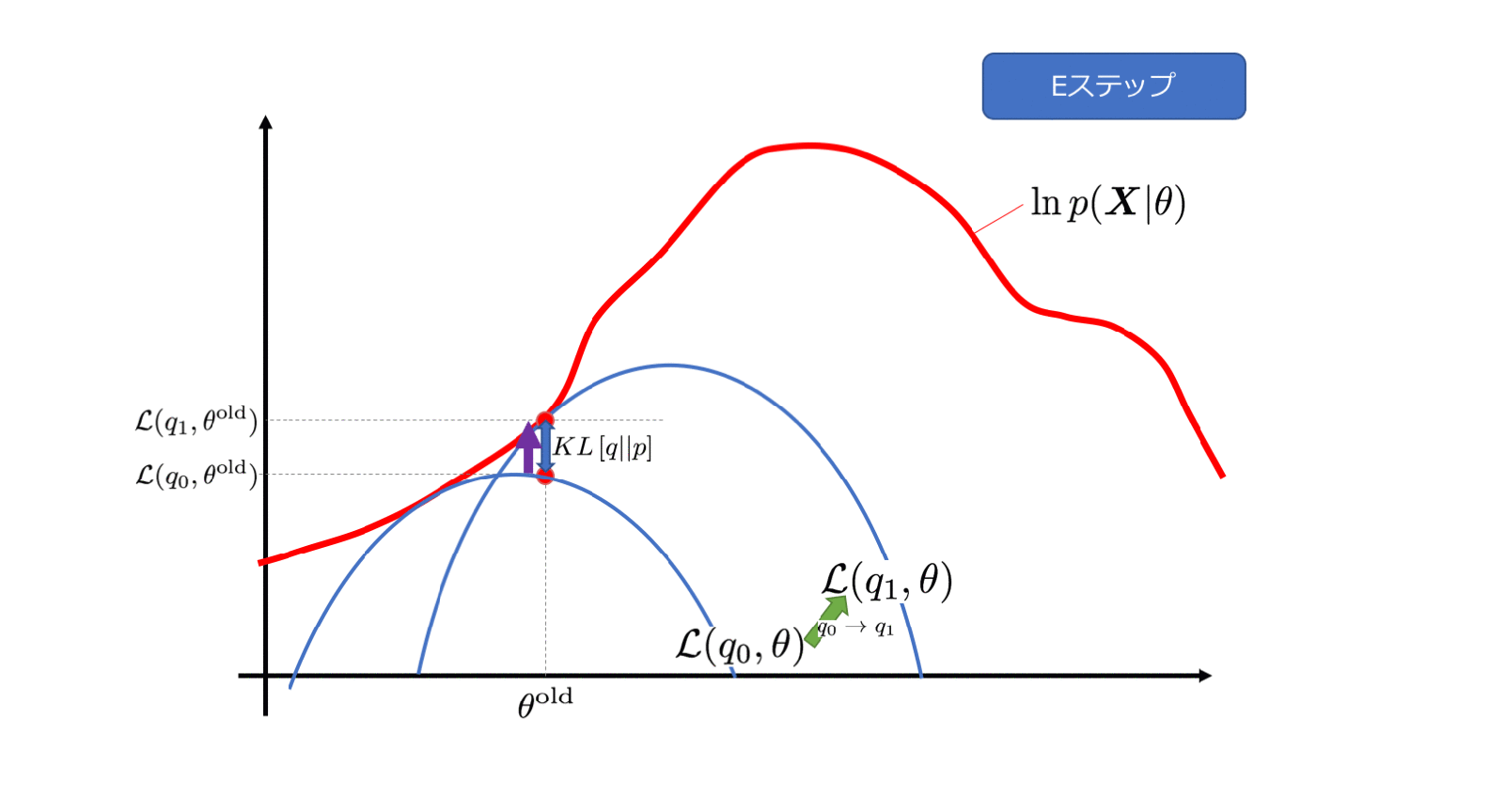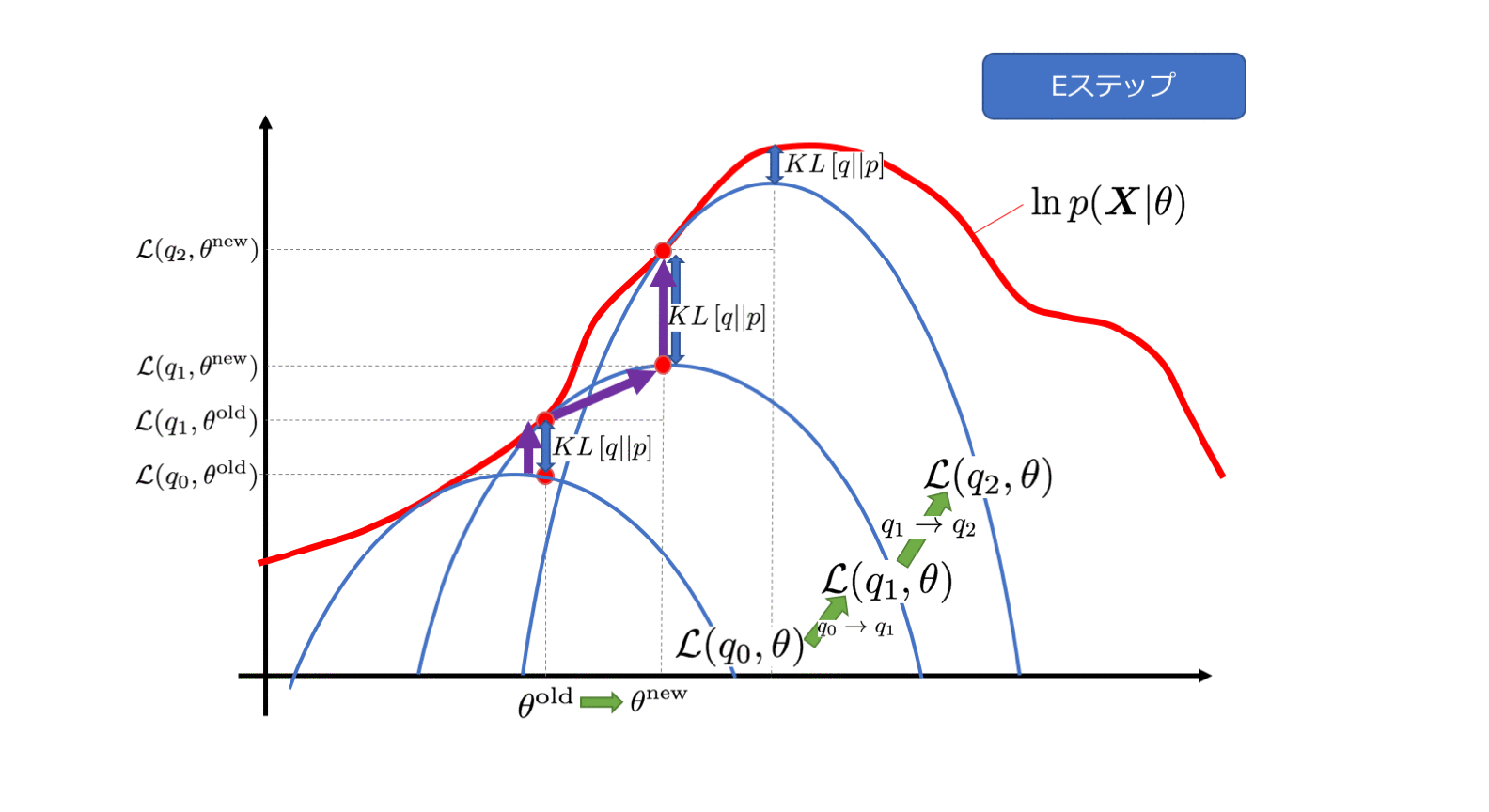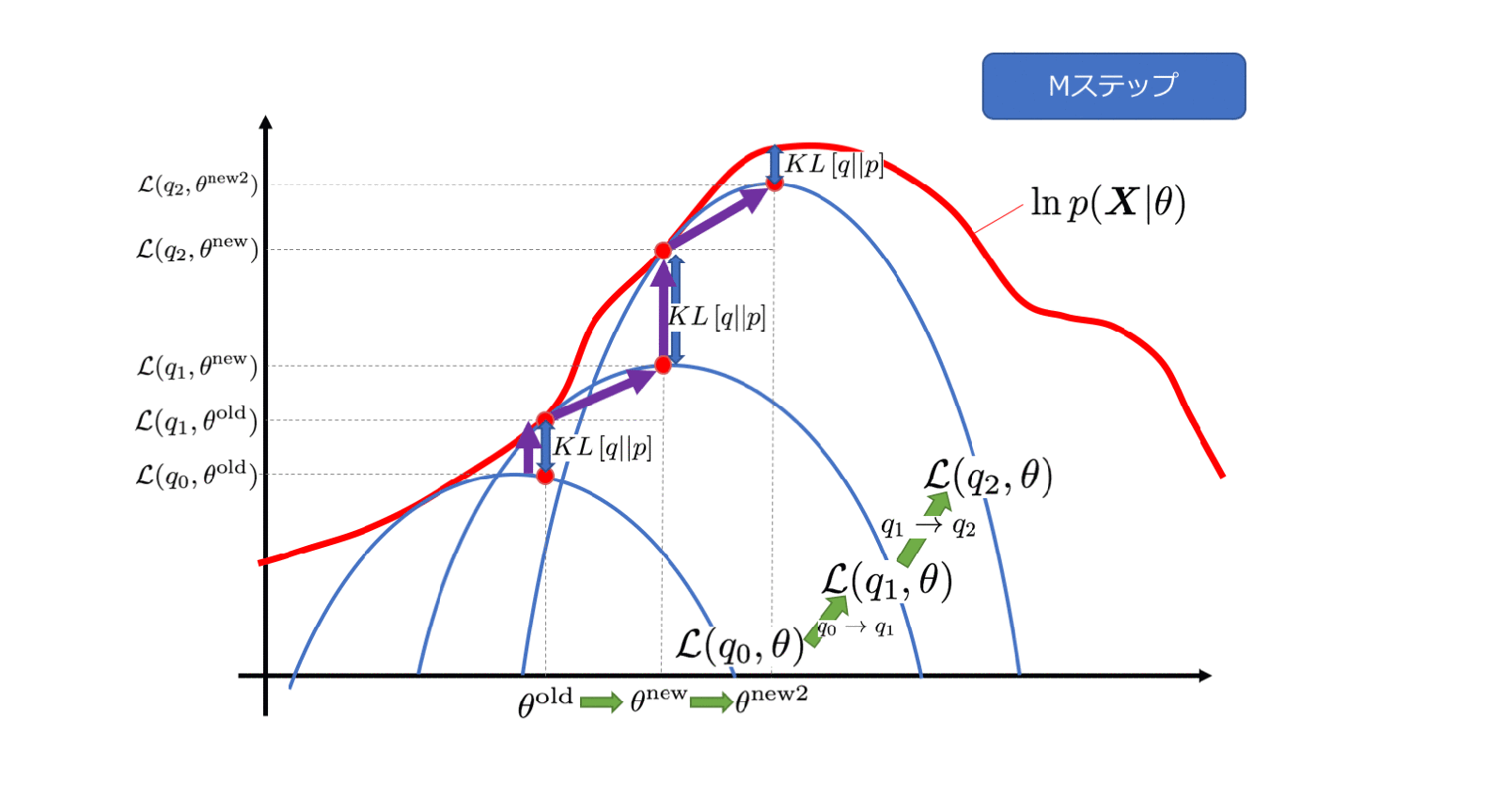
(6)引入了隐函数后，(7)通过条件概率公式变换概率函数，然后就可以得到(10)。这里可以看出，我们是在构造一个隐函数的分布q。因为我们想让似然函数最大，那就是说(10)第二项的KL散度尽可能小，也就是要让构造出来的q尽可能和真实的隐函数分布接近，这时候$q(\mathbf{z})= P(\mathbf{z}|\mathbf{x},\mathbf{\theta})$，KL散度为零。

同时可以看出来刚才的(2)步的让Jensen不等式取等号的操作也是在让KL散度为零构造下限，也就是让$q(\mathbf{z})= P(\mathbf{z}|\mathbf{x},\mathbf{\theta})$取q分布的期望（Expectation）当做隐函数分布的估算。

然后利用q分布再对对数似然函数最大化（Maximization）更新$\theta$。

这个也是所谓的九层境界里面的第二层。（EM算法的九层境界：Hinton和Jordan理解的EM算法）

0x40 GMM混合高斯分布的例子

有空再更新

其他

参考及延伸

[1] PRML

[2] 知乎: 怎么通俗易懂地解释EM算法并且举个例子?:彭一洋的回答有概括性的数学公式

[3] Do, C. B., & Batzoglou, S. (2008). What is the expectation maximization algorithm? Nature Biotechnology, 26(8), 897–899. https://doi.org/10.1038/nbt1406

[4] https://ibug.doc.ic.ac.uk/media/uploads/documents/expectation_maximization-1.pdf

[5] 如何感性地理解EM算法？（抛硬币的详解）

[6] EMアルゴリズム徹底解説

[7] EM算法的九层境界：​Hinton和Jordan理解的EM算法

[8] 机器学习系列-强填EM算法在理论与工程之间的鸿沟（上）

[9] 机器学习系列-强填EM算法在理论与工程之间的鸿沟（下）

վ HᴗP ի