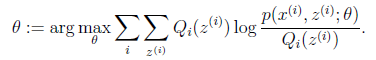EM是一种解决存在隐含变量优化问题的有效方法。EM的意思是“Expectation Maximization”，与最大似然估计MLE的关系，EM是解决（不完全数据的）MLE问题的迭代算法 iterative algorithm。
EM算法的步骤
Note: 通过男女混合高斯模型来记！
初始化分布参数θ； 循环重复直到收敛 { （E步）对于每一个i，计算 #E步骤：根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率，其实就是隐性变量的期望。作为隐藏变量的现估计值： （M步）计算 #将似然函数最大化以获得新的参数值(log式中分母可省略) |
EM收敛
EM的收敛性证明方法确实很牛，能够利用log的凹函数性质，还能够想到利用创造下界，拉平函数下界，优化下界的方法来逐步逼近极大值。而且每一步迭代都能保证是单调的。最重要的是证明的数学公式非常精妙，硬是分子分母都乘以z的概率变成期望来套上Jensen不等式。
Jensen不等式：如果f是凸函数，X是随机变量，那么
。特别地，如果f是严格凸函数，那么
当且仅当
，也就是说X是常量。Jensen不等式应用于凹函数时，不等号方向反向，也就是
。
如果将样本看作观察值，潜在类别看作是隐藏变量，那么聚类问题也就是参数估计问题，只不过聚类问题中参数分为隐含类别变量和其他参数，这犹如在x-y坐标系中找一个曲线的极值，然而曲线函数不能直接求导，因此什么梯度下降方法就不适用了。但固定一个变量后，另外一个可以通过求导得到，因此可以使用坐标上升法，一次固定一个变量，对另外的求极值，最后逐步逼近极值。对应到EM上，E步估计隐含变量，M步估计其他参数，交替将极值推向最大。
EM算法另一种理解
坐标上升法（Coordinate ascent）：
图中的直线式迭代优化的路径，可以看到每一步都会向最优值前进一步，而且前进路线是平行于坐标轴的，因为每一步只优化一个变量。
这犹如在x-y坐标系中找一个曲线的极值，然而曲线函数不能直接求导，因此什么梯度下降方法就不适用了。但固定一个变量后，另外一个可以通过求导得到，因此可以使用坐标上升法，一次固定一个变量，对另外的求极值，最后逐步逼近极值。对应到EM上，E步：固定θ，优化Q；M步：固定Q，优化θ；交替将极值推向最大。
参考https://blog.csdn.net/pipisorry/article/details/42550815