今天我们复习一下线性代数中的矩阵特征分解与奇异值分解。本文将结合几何的角度来阐述这两个概念。
一、特征值与特征分解
假设我们现在有一个对角矩阵为:
将该矩阵作用于列向量,则可以得到:
从几何的角度,上式可以看做在平面上取一个点(x, y)并使用矩阵乘法将其变换为另外一个点。我们可以用下图表示上述变换:
由图中可以看出矩阵M使该平面在横轴方向变大了3倍,纵轴方向保持不变。
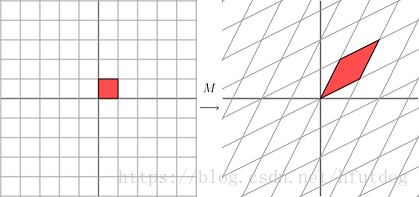
如果矩阵M换作下式是什么情况呢?
变换的效果会像下面这张图一样:
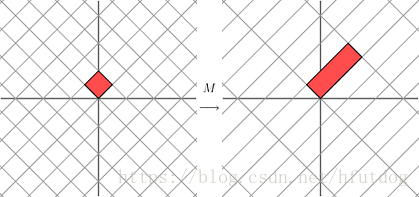
上面的图可能不是很直观,让我们把图片中的网格向左旋转45度观察:
现在,我们能够很明显地看到,M矩阵将向量在一个方向上拉伸了3倍,在另外一个方向上保持不变。在2*2对称矩阵作用下的结果,我们一般都需要通过旋转网格来观察。这样的矩阵一般会使原向量在其两个方向上产生拉伸或者反射,也就是说它对向量的作用和对角矩阵类似。
现在,我们来具体地看特征值和特征向量。
假设我们有一个对称矩阵M,那么我们可以找到一组正交向量使得
是
的常数(标量)倍,即:
也就意味着向量在被矩阵M乘以后发生了拉伸或者反射变换。因为上面的性质,我们把
叫做矩阵M的特征向量,而
叫做矩阵M的特征值。需要注意的是,对应于不同特征值的特征向量相互之间应该是正交的。
结合上面的三张图,也就是我们的向量被矩阵M(M是2*2的)作用,实际上就相当于将该向量旋转到M的两个相互正交的特征向量所在的网格中,然后再对其进行拉伸或者反射变换。还有一点需要的说明的是,虽然我们上面例子中的矩阵M都是对称矩阵,但实际上如果M是非对称矩阵,上述性质也是成立的。
可能这样说明特征值和特征向量还不够直观,那么我们可以考虑拳击的场景。在拳击场景下,特征向量决定了你出拳的方向,特征值就决定了你出拳的力度。
了解了特征值和特征向量后,我们可以很容易地理解特征分解,特征分解就是将一个可对角化的矩阵A分解成如下形式:
其中Q是n阶方阵,且其第i列为 A 的特征向量。
是对角矩阵,其对角线上的元素为对应的特征值,也即
。
这里需要注意的是A为可对角化矩阵,也就是说存在一个可逆矩阵P使得是对角矩阵。
二、奇异值分解
特征分解限制了矩阵的形状和性质,而奇异值分解则适用于任何矩阵,它的几何本质在于对于一个固定形状的矩阵,我们都可以将其从一组正交基(也就是上面三张图中平行四边形旋转前两条边所在的轴)变换到另一组正交基(也就是上面三张图中平行四边形旋转后两条边所在的轴)。
现在我们来具体看一下奇异值分解:
这里M仍然是2维矩阵,我们可以为其找到一组标准正交基和
使得
和
是正交的。然后,我们再使用
和
表示
和
方向上的单位向量,如图所示:
和
的长度用
和
表示,也就是矩阵M的奇异值。因此,我们可以得到下式:
现在,我们可以看一下矩阵M是如何对向量X进行变换的,由于和
是正交单位向量,那么有
也就是:
又因为点积可以转换为向量和向量的转置乘积的形式:
那么就有:
通常上式会被写作:
其中U是一个列由和
组成的矩阵。
是一个对角矩阵,它对角线上的元素是
和
,也就是奇异值。V是一个列由
和
组成的矩阵,它的上标T表示矩阵转置。
这也就表示了如何将矩阵M分解成三个矩阵的乘积,V是一个标准正交基,U是共域的另一组标准正交基,而就表示了如何将V中的向量拉伸变换到向量U。
三、奇异值分解的应用
在人工智能中奇异值分解一般是和PCA(主成分分析)相关的,数据集的特征值(在SVD中用奇异值表征)按照重要性排列,降维的过程就是舍弃不重要的特征向量的过程,而剩下的特征向量构成降维后的空间。比较具体的应用是数据压缩、降噪等。更广泛的应用网络上也有很多文章讲到,这里就不再赘述。
参考资料: