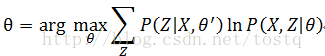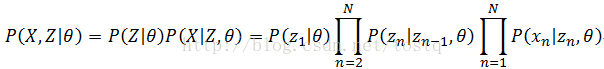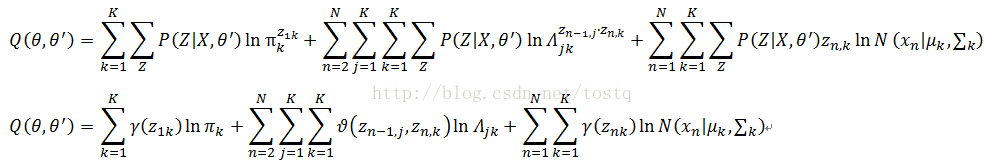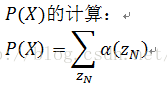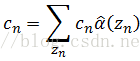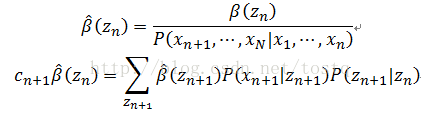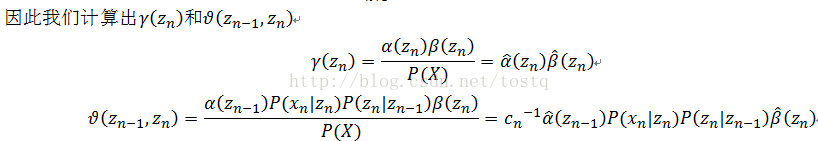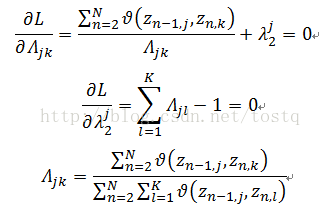隐马尔科夫链HMM的参数θ的EM训练过程
现在回到前一节最后提出的参数θ的最大似然函数上来,先对其做个对数变换,做对数变换是考虑到序列X的概率计算公式中包含了连乘,为了方便计算同时避免序列X的概率过小,因此对其做了对数变换。

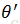
为了方便表示,以下定义:
而
根据HMM的结构定义,其参数θ主要分为三部分:隐藏状态的先验分布π(同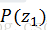
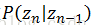

此时综合得出:
这里定义:
1、E步骤
这里定义:
求α的过程,也即所谓的前向算法,具体代码如下(这里增加了一个归一化因子c,下面会具体讲解):
# 求向前传递因子
def forward(self, X, Z):
X_length = len(X)
alpha = np.zeros((X_length, self.n_state)) # P(x,z)
alpha[0] = self.emit_prob(X[0]) * self.start_prob * Z[0] # 初始值
# 归一化因子
c = np.zeros(X_length)
c[0] = np.sum(alpha[0])
alpha[0] = alpha[0] / c[0]
# 递归传递
for i in range(X_length):
if i == 0: continue
alpha[i] = self.emit_prob(X[i]) * np.dot(alpha[i - 1], self.transmat_prob) * Z[i]
c[i] = np.sum(alpha[i])
if c[i]==0: continue
alpha[i] = alpha[i] / c[i]
return alpha, c同理,我们也可以通过后向算法来递归求出β
Python代码
# 求向后传递因子
def backward(self, X, Z, c):
X_length = len(X)
beta = np.zeros((X_length, self.n_state)) # P(x|z)
beta[X_length - 1] = np.ones((self.n_state))
# 递归传递
for i in reversed(range(X_length)):
if i == X_length - 1: continue
beta[i] = np.dot(beta[i + 1] * self.emit_prob(X[i + 1]), self.transmat_prob.T) * Z[i]
if c[i+1]==0: continue
beta[i] = beta[i] / c[i + 1]
return beta另外还可以根据α和β值求出序列X的发生概率
α和β的归一化问题
引入缩放因子:
归一化的α的新求解公式表示为
这里的c非常好求:
因此可以求出
同理:
相关Python代码:
# E步骤
# 向前向后传递因子
alpha, c = self.forward(X, Z) # P(x,z)
beta = self.backward(X, Z, c) # P(x|z)
post_state = alpha * beta
post_adj_state = np.zeros((self.n_state, self.n_state)) # 相邻状态的联合后验概率
for i in range(X_length):
if i == 0: continue
if c[i]==0: continue
post_adj_state += (1 / c[i])*np.outer(alpha[i - 1],beta[i]*self.emit_prob(X[i]))*self.transmat_prob而此时序列X的发生概率可以计算为:
相关Python代码
# 估计序列X出现的概率
def X_prob(self, X, Z_seq=np.array([])):
# 状态序列预处理
# 判断是否已知隐藏状态
X_length = len(X)
if Z_seq.any():
Z = np.zeros((X_length, self.n_state))
for i in range(X_length):
Z[i][int(Z_seq[i])] = 1
else:
Z = np.ones((X_length, self.n_state))
# 向前向后传递因子
_, c = self.forward(X, Z) # P(x,z)
# 序列的出现概率估计
prob_X = np.sum(np.log(c)) # P(X)
return prob_X2、M步骤
解最大似然方程,首先定义拉格朗日式:
求解初始状态概率为:
同理,求解状态转换概率为:
这个过程用Python代码表示:
# M步骤,估计参数
self.start_prob = post_state[0] / np.sum(post_state[0])
for k in range(self.n_state):
self.transmat_prob[k] = post_adj_state[k] / np.sum(post_adj_state[k])均值求解:
同理协方差求解:
相关Python代码:
def emit_prob_updated(self, X, post_state): # 更新发射概率
for k in range(self.n_state):
for j in range(self.x_size):
self.emit_means[k][j] = np.sum(post_state[:,k] *X[:,j]) / np.sum(post_state[:,k])
X_cov = np.dot((X-self.emit_means[k]).T, (post_state[:,k]*(X-self.emit_means[k]).T).T)
self.emit_covars[k] = X_cov / np.sum(post_state[:,k])
if det(self.emit_covars[k]) == 0: # 对奇异矩阵的处理
self.emit_covars[k] = self.emit_covars[k] + 0.01*np.eye(len(X[0]))关于离散概率分布函数的更新,离散概率分布类似于一个表格,观测值x只能包含有限的特定值,而离散概率分布表示为由某状态得到某观测值的概率。由此我们重新定义拉格朗日式,这里增加的一项指某状态生成所有观测值的概率之和应该为1。
然后我们求解离散概率分布函数:
相关Python代码为:
def emit_prob_updated(self, X, post_state): # 更新发射概率
self.emission_prob = np.zeros((self.n_state, self.x_num))
X_length = len(X)
for n in range(X_length):
self.emission_prob[:,int(X[n])] += post_state[n]
self.emission_prob+= 0.1/self.x_num
for k in range(self.n_state):
if np.sum(post_state[:,k])==0: continue
self.emission_prob[k] = self.emission_prob[k]/np.sum(post_state[:,k])
经过EM算法后,可以得到隐马尔科夫的所有参数。
PS:
项目说明:http://blog.csdn.net/tostq/article/details/70846702
代码下载:https://github.com/tostq/Easy_HMM (点星是对作者最好的支持!!!^_^)