1.1.3 后向算法

1.2 根据观测序列预测状态序列

1.2.1 维特比算法（动态规划）

1.3 估计模型参数

参考文献

阐述

隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。

用一个简单的例子来阐述：

假设我手里有三个不同的骰子。

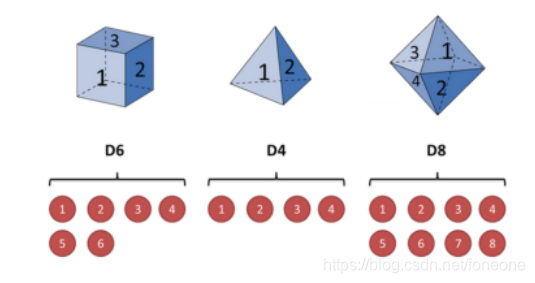
第一个骰子6个面（称这个骰子为D6），每个面（1，2，3，4，5，6）出现的概率是1/6。

第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4。

第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。

假设开始掷骰子，先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。然后掷骰子，得到一个数字：1，2，3，4，5，6，7，8中的一个。不停的重复上述过程，会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。例如可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4

这串数字叫做可见状态链（书中的观测数据）。但是在隐马尔可夫模型中，不仅仅有这么一串可见状态链，还有一串隐含状态链（状态序列）。在这个例子里，这串隐含状态链就是你用的骰子的序列。比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8

一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率（transition probability）。

可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率（emission probability）。就我们的例子来说，六面骰（D6）产生1的输出概率是1/6。

采用《统计学习方法》书上的定义，将上述描述定义如下：

Q为所有可能发生的状态序列（共N个），V是所有可能的观测数列集合（共M个）。

$Q=\left\{q_{1}, q_{2}, \cdots, q_{N}\right\}, \quad V=\left\{v_{1}, v_{2}, \cdots, v_{M}\right\}$

I是长度为T的状态序列，O是对应的观测数据序列。

$I=\left(i_{1}, i_{2}, \cdots, i_{T}\right), \quad O=\left(o_{1}, o_{2}, \cdots, o_{T}\right)$

A是状态转移概率矩阵：

$A=\left[a_{i j}\right]_{N \times N}$

其中， $a_{i j}=P\left(i_{t+1}=q_{j} | i_{t}=q_{i}\right), \quad i=1,2, \cdots, N ; j=1,2, \cdots, N$ ，是在时刻t处于状态 $q_{i}$ 的条件下在时刻t+1转移到状态 $q_{j}$ 的概率。

B是观测概率矩阵：

$B=\left[b_{j}(k)\right]_{N \times M}$

其中， $b_{j}(k)=P\left(o_{t}=v_{k} | i_{t}=q_{j}\right), \quad k=1,2, \cdots, M ; j=1,2, \cdots, N$ ，是在时刻t处于 $q_{j}$ 状态的条件下生成观测序列 $v_{k}$ 的概率。

$\pi$ 是初始状态概率向量：

$\pi=\left(\pi_{i}\right)$

其中， $\pi_{i}=P\left(i_{1}=q_{i}\right), \quad i=1,2, \cdots, N$ ，是时刻t=1处于状态 $q_{i}$ 的概率。

隐马尔可夫模型由初始状态概率向量 $\pi$ ，状态转移概率矩阵A和观测概率矩阵B决定。 $\pi$ 和A决定状态序列，B决定观测序列。因此，隐马尔可夫模型 $\lambda$ 可以用三元符号表示，即

$\lambda=(A, B, \pi)$

隐马尔可夫模型有3个基本问题：

(1)概率计算问题，在给定模型 $\lambda=(A, B, \pi)$ 和观测序列O的情况下，计算在模型 $\lambda=(A, B, \pi)$ 下观测序列O出现的概率 $P(O | \lambda)$ ；知道骰子有几种（隐含状态数量），也知道每种骰子掷出来数字的概率（观测概率矩阵），骰子之间如何转换比如现在是D4，下一个是D4，D6，D8的概率（状态转移概率矩阵），根据掷骰子掷出的结果（观测序列），想知道掷出这个结果（观测序列）的概率。

(2)预测问题（解码问题），已知模型 $\lambda=(A, B, \pi)$ 和观测序列O，求给定观测序列条件概率 $P(I | O)$ 最大的状态序列I ，即给定观测序列，求最有可能的对应的状态序列；骰子有几种（隐含状态数量），也知道每种骰子掷出来数字的概率（观测概率矩阵），骰子之间如何转换（状态转移概率矩阵），根据掷骰子掷出的结果（观测序列），想知道每次（骰子共掷了10次）掷出来的都是哪种骰子（状态序列）

(3)学习问题，已知观测序列O，估计模型参数 $\lambda=(A, B, \pi)$ 参数，使得在该模型下观测序列概率最大 $P(O | \lambda)$ ，用极大似然估计的方法估计参数；知道骰子有几种（隐含状态数量），观测到很多次掷骰子的结果（观测序列），想反推出每种骰子掷出来数字的概率（观测概率矩阵），骰子之间如何转换（状态转移概率矩阵）

1.1 观测序列O出现的概率

1.1.1 穷举法（直接计算法）

通过列举所有可能产生观测序列O的状态，对于各个状态下求解产生观测序列的概率。然后对所有可能的概率求和，可以得到 $P(O | \lambda)$ 。

拿上面的骰子举例子，求最终观测预测为1 6 3 5 2 7 3 5 2 4的概率。

第一步：列举出可能产生此序列的状态，（1）可能序列：D4 D6 D4 D6 D4 D8 D8 D6 D4 D4（2）可能序列：D4 D6 D6 D8 D8 D8 D4 D6 D6 D4....

第二步：计算出产生这些状态的概率，然后在求出这些状态产生1 6 3 5 2 7 3 5 2 4的概率，将对应的状态和产生1 6 3 5 2 7 3 5 2 4的概率相乘（联合概率）

第三步：将所有可能概率求和，得到 $P(O | \lambda)$

上述过程用公式表示为：

状态序列I的概率 $P(I | \lambda)$ 为：

$P(I | \lambda)=\pi_{i_{1}} a_{i_{1} i_{2}} a_{i_{2} i_{3}} \cdots a_{i_{r-1}, i_{r}}$

这个状态下，观测序列O的概率为 $P(O |I, \lambda)$ ：

$P(O | I, \lambda)=b_{i_{1}}\left(o_{1}\right) b_{i_{2}}\left(o_{2}\right) \cdots b_{i_{r}}\left(o_{T}\right)$

O和I同时出现的概率 $P(O ,I| \lambda)$ 为：

$P(O, I | \lambda)=P(O | I, \lambda) P(I | \lambda) =\pi_{i_{1}} b_{i_{1}}\left(o_{1}\right) a_{i_{1} i_{2}} b_{i_{2}}\left(o_{2}\right) \cdots a_{i_{r-1}, i_{T}} b_{i_{r}}\left(o_{T}\right)$

再对所有可能的状态序列I求和，得到观测序列O的概率 $P(O | \lambda)$

$P(O | \lambda)=\sum_{I} P(O | I, \lambda) P(I | \lambda) =\sum_{i_{1}, i_{2}, \cdots, i_{T}} \pi_{i_{1}} b_{i_{1}}\left(o_{1}\right) a_{i_{1} i_{2}} b_{i_{2}}\left(o_{2}\right) \cdots a_{i_{r-1} i_{T}} b_{i_{r}}\left(o_{T}\right)$

但是这样做工作量很大，是 $O\left(T N^{T}\right)$ 阶的，所以利用前向-后向算法。

1.1.2前向算法

这个前向算法的意思就是每次一个状态一个状态的来，假设初始状态为D4，那么下一个状态为D4，D6，D8，的概率分别为1/3，1/3，1/3，下下一个状态为D4的概率为：D4->D4+D6->D4+D8->D4=(1/3)*(1/3)+(1/3)*(1/3)+(1/3)*(1/3)

以此类推，在上述骰子问题中，第n次转移都是计算前n-1次状态累加而成的，所以避免了求解所有的状态概率，节约时间，所以前向算法的复杂度为 $O\left(T N^{2}\right)$ ，简要说明问题可以看下图。

(第一个状态为D4，第二个状态为D4、D6、D8的概率在第一次的基础上计算，第三次的状态为D4、D6、D8又在前一次的基础上计算)

上述过程，用公式表述如下：

首先定义前向概率：（t时刻的部分观测序列为 $o_{1}, o_{2}, \cdots, o_{t}$ ，且状态为 $q_{i}$ 的概率为前向概率）

$\alpha_{t}(i)=P\left(o_{1}, o_{2}, \cdots, o_{t}, i_{t}=q_{i} | \lambda\right)$

可以递推求出前向概率 $\alpha_{t}(i)$ 和观测序列 $P(O | \lambda)$

递推算法如下：

1，初值：

$\alpha_{1}(i)=\pi_{i} b_{i}\left(o_{1}\right)$

2，递推，对于t=1,2,3,...,T-1

$\alpha_{t+1}(i)=\left[\sum_{j=1}^{N} \alpha_{i}(j) a_{j i}\right] b_{i}\left(o_{t+1}\right), \quad i=1,2, \cdots, N$

3，终止

$P(O | \lambda)=\sum_{i=1}^{N} \alpha_{T}(i)$

1.1.3 后向算法

后向算法和前向算法差不多的道理，只不过这是从后往前推导，从最后一个观测序列开始。

定义后向概率：（在t时刻状态为 $q_{i}$ 的，从t+1到T的部分观测序列为 $O_{t+1}, O_{t+2}, \cdots, O_{T}$ 的概率为后向概率）

$\beta_{t}(i)=P\left(o_{t+1}, o_{t+2}, \cdots, o_{T} | i_{t}=q_{i}, \lambda\right)$

（1）最后时刻的所有状态 $q_{i}$ 规定为 $\beta_{T}(i)=1$

$\beta_{T}(i)=1, \quad i=1,2, \cdots, N$

（2）对于t=T-1,T-2,...,1

$\beta_{t}(i)=\sum_{j=1}^{N} a_{i j} b_{j}\left(o_{t+1}\right) \beta_{t+1}(j), \quad i=1,2, \cdots, N$

（3）最终求得的观测概率为

$P(O | \lambda)=\sum_{i=1}^{N} \pi_{i} b_{i}\left(o_{1}\right) \beta_{1}(i)$

1.2 根据观测序列预测状态序列

继续拿上面的骰子举例子，假设最终观测预测为1 6 3 5 2 7 3 5 2 4，求解这个序列所对应的最有可能的状态序列是什么？

1.2.1 维特比算法（动态规划）

维特比算法实际上是用动态规划解马尔科夫模型预测问题，即用动态规划求解概率最大的路径（最优路径）。最优路径求解，必须保证每个路径之间都必须是最优的，否则其中就会有一条路径代替它。

以上面的骰子序列作为例子，假设D4、D6、D8产生1的概率分别为：1/4，1/6，1/8，故1对应的状态序列最优为D4，假设骰子之间转移概率相同，那么6为D6、D8的概率分别为1/6，1/8，因此第二个状态为D6，（如果状态转移概率不同，那么有可能第二个筛子状态为D8的可能性更大），顺着这样的思想依次求解，最终求得最后的状态序列。

上述描述过程，也就是维特比算法的过程，在这个过程中，既求解到了最优路径，又求解到了最大概率。

首先定义两个变量 $\delta$ 和 $\psi$ ，定义在时刻t状态为i的所有单个路径 $\left(i_{1}, i_{2}, \cdots, i_{t}\right)$ 中概率最大值的为

$\delta_{t}(i)=\max _{i_{1}, i_{2}, \cdots, i_{+1}} P\left(i_{t}=i, i_{t-1}, \cdots, i_{1}, o_{t}, \cdots, o_{1} | \lambda\right), \quad i=1,2, \cdots, N$

由上述推导过程可知变量 $\delta$ 的递推公式为，

$\delta_{t+1}(i)=\max _{i_{1}, i_{2}, \cdots, i_{t}} P\left(i_{t+1}=i, i_{t}, \cdots, i_{1}, o_{t+1}, \cdots, o_{1} | \lambda\right)$

$=\max _{1<j<N}\left[\delta_{t}(j) a_{j i}\right] b_{i}\left(o_{i+1}\right), \quad i=1,2, \cdots, N ; t=1,2, \cdots, T-1$

定义在时刻t状态为i的所有单个路径 $\left(i_{1}, i_{2}, \cdots, i_{t}\right)$ 中概率最大的路径的第t-1个结点为：

$\psi_{i}(i)=\arg \max _{1 \leq j \leq N}\left[\delta_{t-1}(j) a_{j i}\right], \quad i=1,2, \cdots, N$

维特比算法过程如下：

（1）初始化（初始状态向量乘以第一个观测 $o_{1}$ ）：

$\delta_{1}(i)=\pi_{i} b_{i}\left(o_{1}\right), \quad i=1,2, \cdots, N$

$\psi_{1}(i)=0, \quad t=1,2,...,N$

（2）递推，对于t=2,3,...,T

$\delta_{t}(i)=\max _{1 \leq j<N}\left[\delta_{t-1}(j) a_{j i}\right] b_{i}\left(O_{t}\right) i=1,2,...,N$

（说明一下：t-1时刻状态[假设D4]乘以转移概率（0.1，0.2, 0.7）那么t时刻的概率分别为0.1，0.2, 0.7；再用t时刻的状态去乘以观测概率矩阵（0.8，0.1,0.1）这个的联合概率乘积中最大才是t时刻的最终状态，因为可能小状态概率对应大观测概率）

记录当前状态：

$\psi_{t}(i)=\arg \max _{1\leqslant j\leqslant N}\left[\delta_{t-1}(j) a_{j i}\right] i=1,2,...,N$

（3）终止：

$P^{*}=\max _{1 \leqslant i \leqslant N} \delta_{T}(i)$

$i_{T}^{*}=\arg \max _{1 \leq i \leq N}\left[\delta_{T}(i)\right]$

（4）最优路径回溯.对于 $t=T-1, T-2, \cdots, 1$

$i_{t}^{*}=\psi_{t+1}\left(i_{t+1}^{*}\right)$

求得的最优路径也就是最可能的状态序列为： $I^{*}=\left(i_{1}^{*}, i_{2}^{*}, \cdots, i_{T}^{*}\right)$

解释一下这里为什么是最优路径回溯：

因为 $\psi_{t}(i)$ 记录的是当前t时刻、状态为i时，第t-1个结点是哪个的状态。用骰子距离，假设t-1时刻D4、D6、D8的状态概率分别为（0.1,0.4,0.5）, $\psi_{t}(D4) =$ max[（0.1,0.4,0.5）*（D4->D4的转化概率、D6->D4的转化概率、D8->D4的转化概率）]，假设这个过程中，D6->D4转化概率最大，故 $\psi_{t}(D4) =$ D6；当计算t时刻，状态为D6的上一个结点时，同理但是此时 $\psi_{t}(D6)$ 可能等于D8。因此 $\psi_{t}(i)$ 仅是记录上一结点到这一节点最大的概率。

当通过 $i_{T}^{*}=\arg \max _{1 \leq i \leq N}\left[\delta_{T}(i)\right]$ 公式，计算出T时刻，状态为i时，就可以利用公式 $i_{t}^{*}=\psi_{t+1}\left(i_{t+1}^{*}\right)$ ，计算出每一次迭代过程存储的最大概率下的上一结点信息，因此这里涉及到一个回溯的过程。

1.3 估计模型参数

用的EM算法。因为状态序列看不见（隐藏变量），只能用观测序列（观测数据）去推导。

先求解函数Q（E步），再极大化求解参数（M步）。

由EM算法的Q函数可以写出如下推导：

$Q(\lambda, \overline{\lambda})=E_{I}[\log P(O,I | \lambda) |O, \overline{\lambda}]$

$=\sum_{\mathbf{I}} \log P(O, I | \lambda) \cdot P(I | O, \overline{\lambda})$

$=\sum_{I} \log P(O, I | \lambda) \cdot \frac{P(O,I | \overline{\lambda})}{P(O | \overline{\lambda})}$

由于 $P(O | \overline{\lambda})$ 对于 $\lambda$ 是一个常数，故（其中 $\overline{\lambda}$ 是上一次迭代出来的，是一个常数， $\lambda$ 是一个变量）：

$Q(\lambda, \overline{\lambda})=\sum_{\mathbb{I}} \log P(O,I|\lambda) \cdot P(O, I | \overline{\lambda})$

由于：

$P(O | \overline{\lambda})=\pi_{i 1} b_{i}(o_{1})a_{i_{1}i_{2}} b_{i_{2}}\left(o_{2}\right)....a_{i_{T-1}i_{T}} b_{i_{T}}({o_{T}})$

故：

$Q(\lambda, \overline{\lambda})=\sum_{I} \log \pi_{i 1} P(O,I| \overline\lambda)+\sum_{I}\left(\sum_{t=1}^{T-1} \log a_{i_{t}} a_{i_{t+1}}\right) \cdot P(O,I | \overline{\lambda})$ $+\sum_{I}\left(\sum_{t=1}^{T-1} \log b_{i_{t}}(o_{t})\right) \cdot P(O,I | \overline{\lambda})$

至此E步完成。构造出来了Q函数，下面就是对Q函数极大化然后更新参数（M步）。

M步：由于模型中有三个参数要求解， $\pi,a,b$ 。并且Q函数里面三个参数是求和的形式，所以求解 $\pi,a,b$ 只取其中一部分就行了。

《统计学习方法》书中给出了 $\pi$ 的求解，所以我列一个a的求解。

由于 $\sum_{j=1}^{N} a_{i j}=1$ （为什么是j不是i呢？可以看一下a状态转移概率矩阵，每一行都是一个状态（t-1时刻）向下一个时刻（t时刻）所有状态转移的概率，所以概率为1）

利用拉格朗日函数求解，构造的拉格朗日函数形式如下：

$\sum_{t=1}^{T} \sum_{i=1}^{N} \sum_{j=1}^{N}\log _{a_{i j}}\log _{a_{i j}}P(O,i_{t}=i,i_{t+1}=j|\overline\lambda)+\gamma \left(\sum_{j=1}^{n} a_{i j-1}\right)$

对上式 $a_{i j}$ 求导数得，

$\frac{P\left(O, i_{t}=i, i_{t+1}=j | \overline\lambda\right)}{a_{i j}}+\gamma =0$

即

${P\left(O, i_{t}=i, i_{t+1}=j | \overline\lambda\right)}+\gamma{a_{i j}} =0$ （1）

对上式所有j求和可得：

$\gamma=-P(O, i_{t}=i |\overline{\lambda})$

把上述结果带入（1）可得：

$a_{ij}=\frac{\sum_{t=1}^{T-1} P\left(O, i_{t}=i, i_{t+1}=j | \overline{\lambda}\right)}{\sum_{t=1}^{T-1} P\left(O, i_{t}=i | \overline{\lambda}\right)}$

以上述同样的方法也可以求解出其他两个变量：

$\pi_{i}=\frac{P\left(O, i_{1}=i| \overline\lambda\right)}{P(O=i |\overline{\lambda})}$

$b_{j}(k)=\frac{\sum_{t=1}^{N}P\left(O, i_{t}=j )I(o_{t}=v_{k})| \overline\lambda\right)}{\sum_{t=1}^{N}P(O, i_{t}=j |\overline{\lambda})}$ 、

扩展：

（1）给定模型 $\lambda$ 和观测序列O，在时刻t处于状态 $q_{i}$ 的概率，记为：

$\gamma_{t}(i)=P\left(i_{i}=q_{i} | {O}, \lambda\right)=\frac{P\left(i_{t}=q_{i}, O | \lambda\right)}{P(O | \lambda)}$

由前向概率和后向概率定义可知，

${\alpha_{t}(i) \beta_{t}(i)}=P\left(i_{t}=q_{i}, O | \lambda\right)$

故

$\gamma_{t}(i)=\frac{\alpha_{t}(i) \beta_{t}(i)}{P(O | \lambda)}=\frac{\alpha_{t}(i) \beta_{t}(i)}{\sum_{j=1}^{N} \alpha_{t}(j) \beta_{t}(j)}$

即利用 $\gamma_{t}(i)$ 刻画，单个时刻的状态概率。

（2）给定模型 $\lambda$ 和观测序列O，在时刻t处于状态 $q_{i}$ 的概率，t+1时刻处于 $q_{j}$ 的状态概率为：

$\xi_{t}(i, j)=P\left(i=q_{i}, i_{t+1}=q_{j} | O, \lambda\right)$

利用上述方法有，

$\xi_{t}(i, j)=\frac{P\left(i_{i}=q_{i}, i_{t+1}=q_{j}, O | \lambda\right)}{P(O | \lambda)}=\frac{P\left(i_{t}=q_{i}, i_{i+1}=q_{j}, O | \lambda\right)}{\sum_{i=1}^{N} \sum_{j=1}^{N} P\left(i_{t}=q_{i}, i_{t+1}=q_{j}, O | \lambda\right)}$

$P\left(i_{t}=q_{i}, i_{i+1}=q_{j}, O | \lambda\right)=\alpha_{i}(i) a_{i} b_{j}\left(o_{i+1}\right) \beta_{i+1}(j)$

$\xi_{i}(i, j)=\frac{\alpha_{i}(i) a_{i j} b_{j}\left(o_{t+1}\right) \beta_{t+1}(j)}{\sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{t}(i) a_{i j} b_{j}\left(o_{t+1}\right) \beta_{t+1}(j)}$

因此在利用学习算法（EM）算法求解出各个参数后，

可以进行进一步化简表示，即

$a_{i j}=\frac{\sum_{t=1}^{T-1} P\left(O, i_{t}=i, i_{t+1}=j | \overline{\lambda}\right)}{\sum_{t=1}^{T-1} P\left(O, i_{t}=i | \overline{\lambda}\right)}=\frac{\sum_{i=1}^{T-1} \xi_{t}(i, j)}{\sum_{i=1}^{T-1} \gamma_{t}(i)}$ （1）

$b_{j}(k)=\frac{\sum_{i=1}^{T} P\left(O, i_{t}=j | \overline{\lambda}\right) I\left(o_{t}=v_{k}\right)}{\sum_{i=1}^{T} P\left(O, i_{t}=j | \overline{\lambda}\right)}=\frac{\sum_{t=1,o_{t}=v_{k}}^{T} \gamma_{t}(j)}{\sum_{t=1}^{T} \gamma_{t}(j)}$ （2）