Second paper:《Auto-encoding Variational Bayes》自编码变分贝叶斯的阅读笔记

这是生成模型下面阅读的second paper：

论文地址：[1312.6114] Auto-Encoding Variational Bayes

来源：arXiv:1312.6114v10 [stat.ML] 1 May 2014

参考文章链接：https://zhuanlan.zhihu.com/p/37224492

1 介绍

在涉及如下图所示的包含隐变量的学习和推理问题时，往往会遇到后验概率不可计算的情况，这会导致参数难以学习以及推理难以进行。下边的问题基于下图所示的概率图进行讨论，其中 $N$ 表示样本集大小， $x$ 表示观察变量， $z$ 表示隐含变量，生成模型表示为 $p_{\theta}(z)p_{\theta}(x|z)$ ， $q_{\phi}(z|x)$ 是对 $p_{\theta}(z|x)$ 的近似，表示识别模型。

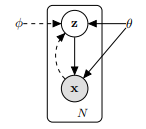
观察变量及隐变量概率图

注：从x到z是inference model（encoder）,从z到x是generative model (decoder),对于在生成模型这一部分中 $p_{\theta}(z|x)$ 是生成模型的后验概率。而对于实际的生成模型中这一后验概率往往是不可计算的，所以需要根据假设分布来进行近似，再利用KL散度来刻画这两个分布的相似度（最小化）。这也是斯坦福Ermon教授的EM[1]----EM[2]-----EM[3]中提到的逐次进行近似刻画。

2 Problem

2.1不可计算问题

如果对概率图所示的随机变量 $X$ 、 $Z$ 进行建模，便得到生成模型 $P_{\theta}(Z)P_{\theta}(X|Z)$ ：

遍历样本得到对数似然函数： $Objective=\sum_{i=1}^{N}{log(p_{\theta}(x^{(i)}))}$ ，先验概率的计算公式为 $p_{\theta}(x)=\int_{}^{}p_{\theta}(z)p_{\theta}(x|z)dz$ ，如果公式不可以写成有限运算的形式，则不可计算，故无法通过ML算法进行参数优化，同时 $p_{\theta}(z|x)=p_{\theta}(x,z)/p_{\theta}(x)$ 中含有先验概率也不可计算，故无法使用EM算法对参数进行优化以及进行所有基于后验概率的推理。为了解决这个问题，论文提出了 $AEVB$ (自编码变分贝叶斯)算法，采用 $q_{\phi}(z|x)$ 近似 $p_{\theta}(z|x)$ 同时把最大化似然函数下界作为目标函数的方法，巧妙地避开了后验概率计算。

2.2 数据集问题：一个大数据集：我们有大量的数据，批处理优化成本太高;我们希望使用小型的小批量甚至单个的数据点来进行参数更新。基于采样的解决方案，例如MC-EM，但是一般来说太慢了，因为它涉及到每个数据点的一个典型的昂贵的采样循环。

3 似然函数下界

对 $Objective$ 中的一项 $log(x^{(i)})$ 进行推导得到：

$log(x^{(i)})=D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x))+L(\theta,\phi;x^{(i)})$

$L(\theta,\phi;x^{(i)})=-D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z))+E_{q_\phi(z|x^{(i)})}logp_\theta(x^{(i)}|z)\\ =E_{q_\phi(z|x^{(i)})}log(p_\theta(x^{(i)},z))+H_{q_\phi(z|x^{(i)})}(z)$

由于 $D_{KL}>=0$ 恒成立，故 $L(\theta,\phi;x^{(i)})$ 是似然函数对应 $x^{(i)}$ 项的下界，可见该下界的计算不需要涉及后验概率 $p_\theta(z|x^{(i)})$ 的计算，所以是可计算的，论文通过最大化该下界来进行参数的学习。

4 SGVB estimator(随机梯度变分贝叶斯估计器)

由于 $L(\theta,\phi;x^{(i)})$ 存在无法直接计算梯度的项比如 $E_{q_\phi(z|x^{(i)})}logp_\theta(x^{(i)}|z)$ 和 $E_{q_\phi(z|x^{(i)})}log(p_\theta(x^{(i)},z))$ ，一般采用Monte Carlo方法进行计算： $\bigtriangledown_{\theta}E_{p_\theta(z)}f(z)=E_{p_{\theta}(z)}\bigtriangledown_{\theta}log(p_\theta(z))f(z)\simeq\frac{1}{L}\sum_{l=1}^{L}{\bigtriangledown_{\theta}log(p_\theta(z^{(l)}))f(z^{(l)})}$

其中 $z^{(i)}\sim{p_\theta(z)}$ ，所以可以得到可计算梯度的 $\tilde{L}(\theta,\phi;x^{(i)})$ ，其中 $z^{(i,l)}\sim{q_\phi(z|x^{(i)})}$ :

$L(\theta,\phi;x^{(i)})\simeq\tilde{L}(\theta,\phi;x^{(i)})=-D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z))+\frac{1}{L}\sum_{l=1}^{L}logp_\theta(x^{(i)}|z^{(i,l)})\\ =\frac{1}{L}\sum_{l=1}^{L}log(p_\theta(x^{(i)},z^{(i,l)}))+H_{q_\phi(z|x^{(i)})}(z)$

由前人研究发现，在使用Monte Carlo方法计算梯度时，应该尽量减少分布的方差，故论文中采取了参数重构技巧，即令 $z^{(i)}=g_\phi(\varepsilon,x^{(i)})$ ，其中g为一个以 $\phi$ 为参数的二元函数，以 $\varepsilon\sim{p}(\varepsilon)$ 对 $\varepsilon$ 进行采样得到 $\varepsilon^{(l)}$ ，计算得到 $z^{(i,l)}=g_\phi(\varepsilon^{(l)},x^{(i)})$ ，这就是论文提出的SGVB estimator。论文还发现，当batch size足够大（=100）时，L=1即可。

5 VAE

当通过NN对AEVB中的概率进行建模时，便得到VAE模型，模型图如下：

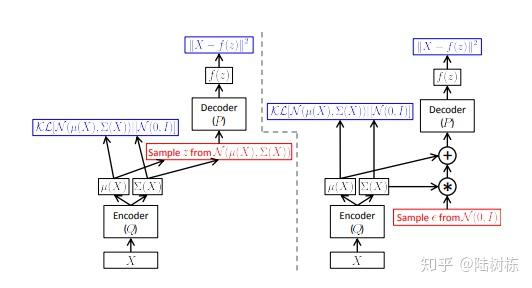
VAE：左侧为不进行参数重构，右侧进行了参数重构

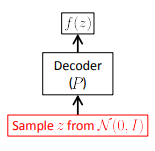
VAE：随机生成数据

模型反映了使用了如下形式的SGVB estimator：

$\tilde{L}(\theta,\phi;x^{(i)})=-D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z))+\frac{1}{L}\sum_{l=1}^{L}logp_\theta(x^{(i)}|z^{(i,l)})\\$

模型假设 $q_\phi(z|x^{(i)})、p_\theta(z)$ 均满足高斯分布，当 $L=1$ 时，第二项表示的是重构误差，故可以使用 $||x^{(i)}-f(z^{(i)})||^2$ 来优化，同时计算可知 $D_{KL}(N(\mu,\delta)||N(0,1))=0.5\times(1 + 2\times{log}(\delta)-\mu^2- \delta^2)$

通过SGD可以对参数进行优化。

6 实验结果

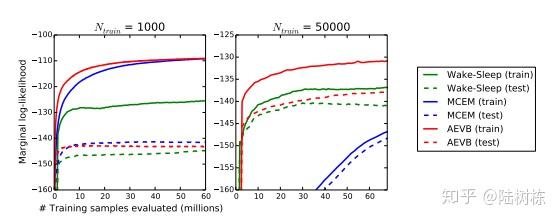
不同训练数据数据量：Wake-Sleep、MCEM、AEVB

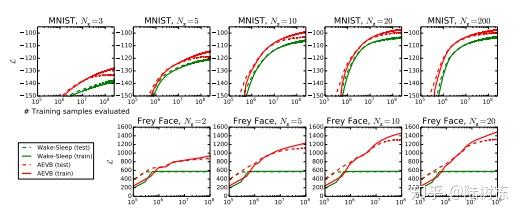
不同隐向量维度：Wake-Sleep、AEVB

Mnist训练后，模型随机生成的数字

7 总结

虽然是一篇很早的论文，但其中涉及到多种技巧，包括概率近似、优化似然函数下界、Monte Carlo采样以及参数重构等，很值得学习。

针对paper的总结：生成模型是由z（潜在隐变量）到x的模型，但是在刻画该模型时会遇到后验概率 $p_{\theta}(z|x)$ intractable，所以引入了inference model生成 $q_{\phi}(z|x)$ 用来近似该后验概率分布 $p_{\theta}(z|x)$ 。

在第二章首先介绍了问题场景----变分下界函数----SGVB估计器和AEVB算法----重参数化技巧

有了变分下界之后，则变成了关于变分参数和生成参数来对变分下界函数L()进行优化；而关于参数求梯度时，采用了MC算法，再将MC算法带入不同的变分下界函数得到不同的SGVB（A and B）估计器，这即是AEVB算法；原本不可导，但利用了重参数化技巧之后，根据MC就可以实现对推理部分（inference model）的参数进行求导。

对于推理模型中的从x到z的采样概率，可以找到一个可微的变换g()和一个辅助变量eplison,再利用重参数化技巧，这样既实现了生成模型中的不可计算的后验概率的估计，并且在更新过程中还可导。

第三章介绍了自编码变分贝叶斯（AEVB）的特例----VAE