[洛谷P4769][BZOJ5416][UOJ#394][NOI2018]冒泡排序（dp+树状数组+组合数学）

Address

https://www.luogu.org/problemnew/show/P4769
https://www.lydsy.com/JudgeOnline/problem.php?id=5416
https://www.lydsy.com/JudgeOnline/upload/noi2018day1.pdf
http://uoj.ac/problem/394

Solution

网上有各种不同的题解，来写一发自己的思路。
一道打表找规律好题

感觉题解比代码还长
首先通过 (zhao) 证 (gui) 明 (lv) ，可以得到：
一个排列的操作数达到下界，
当且仅当该排列不存在任意一个长度大于等于 $3$ 的下降子序列。
一个不严谨的证明：
设第一个数为 $x$ ， $x$ 右边第一个比 $x$ 的位置为 $d$ 。
那么第一轮排序会把 $x$ 移到位置 $d-1$ ，
原先 $[2,d]$ 位置区间内的数整体左移，相对顺序不变。
由于操作数达到下界相当于每次交换的两个数都朝着自己的方向移动，
故只有 $[2,d]$ 内按顺序填着 $[1,d-1]$ 内的数才合法。
以此类推，得出结论。
这证明确实不严谨，还是打表找规律快且简单
这种题当然要从下往上考虑，从暴力推出正解啦。
先考虑 $i=p_i$ （不考虑字典序）及 $n\le 1000$ 。
首先，通过一定的规律可以发现，长度为 $n$ 的排列第一个数为 $1$ 和 $2$ 时方案数相同，为 $3$ 时明显没有为 $2$ 时多，为 $4$ 时方案数继续下降，…，为 $n$ 时只有 $1$ 个合法方案。
我们可以设 (luan) 计 (gao) 出一个状态：
$f[i][j]$ 表示 $i$ 个数的排列，以 $j$ 为开头，合法方案数。
继续利用爆搜打出 $1\le j\le i\le10$ 的 dp 值。
可以通过找规律，得出：

$$f[1][1]=1$$
$$\forall i\ge j\ge2,f[i][j]=\sum_{k=j-1}^{i-1}f[i-1][k]$$
$$\forall i\ge 2,f[i][1]=\sum_{k=1}^{i-1}f[i-1][k]$$
利用前缀和优化，我们解决了 $n\le 1000$ 且 $i=p_i$ 的数据。
如果对字典序有限制，我们就必须要证明。
首先如果第 $1$ 个数为 $1$ ，那么后面的 $i-1$ 个数只要不产生长度大于等于 $3$ 的下降子序列即可。（ $1$ 无法作为长度为 $3$ 的下降子序列的第一个数）
如果把后面 $i-1$ 个数同时减去 $1$ ，那么后 $i-1$ 个数构成了一个合法的 $i-1$ 个数的排列。
如果第 $1$ 个数为 $j$ ，我们分情况讨论：
（1）如果第 $2$ 个数 $\in(1,j)$ ，那么 $1$ 一定出现在第 $2$ 个数的右边，这样第 $1$ 个数 $j$ 、第 $2$ 个数、以及 $1$ 构成了一个长度为 $3$ 的下降子序列。不合法。
（2）如果第 $2$ 个数 $\in(j,i]$ ，那么如果第一个数右边存在两个值 $x,y$ 可以和 $j$ 构成下降子序列，那么第二个数也一定能和 $x,y$ 构成下降子序列（第二个数大于第一个数）。如果把从第二个数开始的所有大于 $j$ 的数都减一，那么后 $i-1$ 个数一定构成了一个合法排列，首位数的取值为 $[j,i-1]$ 。
（3）如果第 $2$ 个数为 $1$ ，就比较难讨论了。但思考一下，这时候后面的数满足的条件为： $[1,j-1]$ 范围的数按照相对顺序出现。也就是说， 数 $2$ 在 $1$ 后面出现，数 $3$ 在 $2$ 后面出现，…，数 $j-1$ 在 $j-2$ 后面出现，但不一定出现在序列的一段连续区间内。同样地，如果把从第二个数开始的所有大于 $j$ 的数都减掉 $1$ ， 并把 $1$ 移到 $2$ 的所在位置， $2$ 移到 $3$ 所在的位置，…， $j-1$ 移到 $1$ 的所在位置，那么这样得到的排列就是一个 $i-1$ 个数的排列，并且第一个数为 $j-1$ 。同样地，我们证了必要性后也可以用差不多的方法证充分性。于是第 $2$ 个数为 $1$ 时的贡献为 $f[i-1][j-1]$ 。
至此，我们已经证完了转移方程。
开始考虑字典序限制。
我们知道， $f[i][j]$ 可以从 $f[i-1][k]$ 转移，其中 $k\in[\max(1,j-1),i-1]$ 。
其中如果 $k$ 为 $\max(1,j-1)$ ，那么表示从「第 $2$ 个数为 $1$ 」转移，否则表示从「第 $2$ 个数为 $k$ 转移 」。
注意：下面我们把 $f[i][j]$ 广义化：表示 $i$ 个不同的数的排列，第一个数排名为 $j$ 的方案数， $rk_i$ 的定义为 $p$ 在位置区间 $[i,n]$ （以 $i$ 为开头的后缀）内 $i$ 位置上数的排名。当然， $rk_1=p_1$ 。
做法：首先考虑 $f[n][...]$ 。
对于 $i>rk_1$ ，根据字典序的定义，如果排列的第 $1$ 个数填了 $i$ ，那么之后不管怎么填字典序都不会小于等于 $p$ 。
而对于 $i=rk_1$ ，我们需要继续去寻求 $j>rk_2$ ，让第二个数填 $j$ 。
于是从 $f[n][i]$ 向上走，转移到 $f[n-1][\max(1,i-1)...n-1]$ 继续处理。
但这一步 $j$ 的取值只能是 $1∪(\max(1,i-1)+1,n-1]$ 。
同样把 $j>rk_2$ 和 $j=rk_2$ 分开处理，如果 $j>rk_2$ ，那么直接把 $f[n-1][j]$ 加入即可。
如果 $rk_2=1$ ，那么从 $f[n-1][\max(1,i-1)]$ 向上一层转移。
否则在 $f[n-1][rk_2]$ 向上一层转移。
必须注意 $rk_x=1$ 时向上转移的方式，如上。
本蒟蒻的代码里使用总方案数减去了字典序小于等于 p 的方案数，请见谅
像这样从下往上 迭代转移，就能统计答案。
我们实现了 $O(Tn^2)$ 的复杂度，可以得到 80 分。
为了拿到 100 分，我们先解决掉俩小问题：
（1）求 $rk_i$ 使用树状数组，就可以把单次求 $rk$ 的复杂度降到 $O(\log n)$ 。
（2）上面的过程中，我们对于每一层（第一维下标） $f$ 其实都是进行了一次区间求和。我们记录下 $f$ 每一层的前缀和即可快速求得 $f$ 某一层的区间和。同时，我们从 $f$ 的转移方程里可以知道， $f$ 的某一层内的区间和，就是下一层的单点值。
这两个小问题解决了，我们就剩下一个待解决的问题：
前面的 $f$ 是要通过平方的时间预处理的，但是实际上会用到的 dp 值只有 $O(Tn)$ 个。故我们考虑如何单点快速求 $f$ ，即 $f$ 的通项公式。
我们之前打出 $f$ 的时候忘记说了一个性质：
$$f[i][1]=Catalan(i+1)$$
$Catalan$ 表示卡特兰数。
预处理阶乘及其逆元即可。
但我们要求的不仅仅是 $f[i][1]$ ，
故我们还是要证明为什么 $f$ 是卡特兰数。
我们注意到 $f$ 的转移中用到的其他 dp 值个数为 $O(n)$ 级别。
故考虑记录 $s[i][j]$ 表示 $f$ 第 $i$ 层的后缀和：
$$s[i][j]=\sum_{k=j}^if[i][k]$$
根据上面，我们有 $s[n][1]=Catalan(n)$ 。
这样转移方程就简化了：
$$s[1][1]=1$$
$$\forall i\ge j\ge2,s[i][j]=s[i-1][j-1]+s[i][j+1]$$
$$\forall i\ge 2,s[i][1]=s[i-1][j]+s[i][j+1]$$
这是一个显然的路径模型！
$s[i][j]$ 可以看做从 $(1,1)$ 出发，每一步走的规则如下：
（1）可以往右上 45 度走 $\sqrt2$ 个长度单位（ $x$ 坐标和 $y$ 坐标各加 $1$ ）
（2）可以往下走（ $y$ 坐标减 $1$ ）
（3）如果当前 $y$ 坐标为 $1$ （触碰直线 $y=1$ ），那么可以往右走（ $x$ 坐标加 $1$ ）
（4）不得走到直线 $y=1$ 的下方。
走到 $(n,1)$ 的方案数。

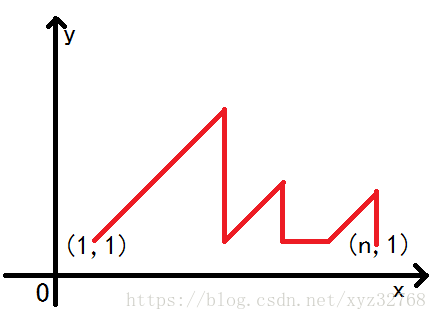
发现规则（3）让我们很难推出性质。
所以我们把 $0$ 扩充进 $i,j$ 的取值，规定 $s[0][0]=1,s[i][0]=s[i][1]$ （ $i>0$ ）
那么所有的转移都被整成一样的，不会有（3）那样 GAYGAY 的条件：
$$s[i][j]=s[i-1][j-1]+s[i][j+1]$$
我们的走法也简单了。
从 $(0,0)$ 走到 $(n,0)$ ，
（1）可以向右上 45 度走 $\sqrt2$ 个长度单位或者向下走 $1$ 个长度单位。
（2）不得越到 $x$ 轴的正下方。
求方案数。

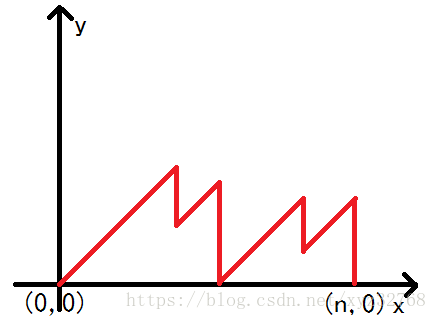
为了使 $x$ 坐标 $+=n$ ，我们要使用 45 度走法走 $n$ 步，但这样导致 $y$ 坐标加一了 $n$ 次，故我们还要使用向下走的操作 $n$ ，才能到达 $(n,0)$ 。
这相当于在 $2n$ 步中选出 $n$ 步向下走。方案数 $C_{2n}^n$ 。
如何去除掉越到 $x$ 轴下方（触碰直线 $y=-1$ ）的方案数呢？
显然，走了 $k$ 步之后，到达点的 $y$ 坐标为前 $k$ 步中， 45 度的步数减去向下的步数。
把操作序列转化成 01 序列， $0$ 表示走 45 度， $1$ 表示向下走，显然这是一个 Catalan 序列，即任意前缀中 $0$ 的个数都 $\ge$ $1$ 的个数的长度为 $2n$ 的序列。
对于一个不合法的序列，我们可以找到第一个满足 $0$ 的个数 $+1=$ $1$ 的个数的前缀 $[1,k]$ 。
将 $[1,k]$ 内的数全部取反，我们得到了一个 $n+1$ 个 $0$ 和 $n-1$ 个 $1$ 构成的序列。
于是有：
$$s[n][0]=Catalan(n)=C_{2n}^n-C_{2n}^{n-1}$$
拓展到一般情况：
$$s[n][m]=C_{2n-m}^{n-m}-C_{2n-m}^{n-m-1}$$
至此，我们实现了单点求 $s$ ，故查询一个 $f$ 值可以在线性预处理阶乘及其逆元后 $O(1)$ 求出。
由于求 $rk$ 时要用树状数组，故复杂度 $O(Tn\log n)$ 。

Code

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define For(i, a, b) for (i = a; i <= b; i++)
#define Rof(i, a, b) for (i = a; i >= b; i--)
using namespace std;
inline int read() {
    int res = 0; bool bo = 0; char c;
    while (((c = getchar()) < '0' || c > '9') && c != '-');
    if (c == '-') bo = 1; else res = c - 48;
    while ((c = getchar()) >= '0' && c <= '9')
        res = (res << 3) + (res << 1) + (c - 48);
    return bo ? ~res + 1 : res;
}
const int N = 6e5 + 5, M = 12e5 + 5, ZZQ = 998244353;
int n, a[N], fac[M], inv[M], A[N], rk[N];
int C(int n, int m) {
    return 1ll * fac[n] * inv[m] % ZZQ * inv[n - m] % ZZQ;
}
int sum(int n, int m) {
    return (C((n << 1) - m, n - m) - C((n << 1) - m, n - 1 - m) + ZZQ) % ZZQ;
}
void change(int x, int v) {
    for (; x <= n; x += x & -x)
        A[x] += v;
}
int ask(int x) {
    int res = 0;
    for (; x; x -= x & -x) res += A[x];
    return res;
}
void work() {
    int i, j, lst = 1, ans = 0;
    n = read();
    if (!n) return (void) puts("0");
    For (i, 1, n) a[i] = read(), A[i] = 0;
    Rof (i, n, 1) change(a[i], 1), rk[i] = ask(a[i]);
    For (i, 1, n) {
        if (lst < rk[i]) ans = (ans + (sum(n - i + 1, lst) -
            sum(n - i + 1, rk[i]) + ZZQ) % ZZQ) % ZZQ, lst = rk[i];
        else if (rk[i] > 1) {
            ans = (ans + sum(n - i, lst - 1)) % ZZQ;
            break;
        }
        else if (i == n) ans = (ans + 1) % ZZQ;
        if (lst > 1) lst--;
    }
    printf("%d\n", (sum(n, 0) - ans + ZZQ) % ZZQ);
}
int main() {
    int i, j, T = read();
    fac[0] = inv[0] = inv[1] = 1;
    For (i, 1, 1200000) fac[i] = 1ll * fac[i - 1] * i % ZZQ;
    For (i, 2, 1200000) inv[i] = 1ll * (ZZQ - ZZQ / i) * inv[ZZQ % i] % ZZQ;
    For (i, 1, 1200000) inv[i] = 1ll * inv[i] * inv[i - 1] % ZZQ;
    while (T--) work();
    return 0;
}