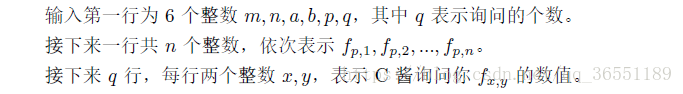【JZOJ5622】【NOI2018模拟4.2】table（组合数学）

Problem

Input

Output

Hint

Solution

40points

　　前8个点的n和m较小，可以直接暴力求出数表中的每个数。
　　时间复杂度：$O(nm)$。

Code

　　Code就不贴了，毕竟后面的60points方法也有这部分。

60points

　　我们考虑第9~12个点，即p=1的情况。
　　当m=4，n=5时，设第1行的5个数分别为A、B、C、D、E。则数表为：
　　

$$\begin{array}{c|lcr} _m\setminus ^n & \text{1} & \text{2} & \text{3} & \text{4} &\text{5}\\ \hline 1 & A & B & C & D & E \\ 2 & aA & aB+bA & aC+bB & aD+bC & aE+bD \\ 3 & a^2A & a^2B+2abA & a^2C+2abB+b^2A & a^2D+2abC+b^2C & a^2E+2abD+b^2C \\ 4 & a^3A &a^3B+3a^2bA & a^3C+3a^2bB+3ab^2A & a^3D+3a^2bC+3ab^2B+b^3A & a^3E+3a^2bD+3ab^2C+b^3B \end{array}$$
　　由表可知，第i行的系数其实就等于 $(a+b)^i$所得系数，也即杨辉三角。f[i][j]的第一个未知数其实就为f[1][j]，第二个为f[1][j-1]，以此类推。但是从f[3][2]可得，它的系数应为{1,2,1}，但是j不足3，所以它的系数就只为前两项。
　　所以，我们知道，杨辉三角其实就等于组合数，我们可以用阶乘以及阶乘的逆元快速求出系数。这样一来，我们就可以用 $O(n)$的时间（因为它最多有n个系数）求出某个位置的值。
　　但是为什么是这样呢？观察f[2][2]可知，它为aB+bA，所以可以运用逆向思维，即每个数都对它的下方产生a倍的贡献，对它的右下方产生 $b$倍的贡献。那么我们可以无视除第1行以外的数，因为如果有某个这种数对其下方和右下方造成了贡献，那么它本身也是由第1行的数累成的，所以相当于第1行的数对其下方和右方造成了贡献。
　　因此，对于x>p，有： $$f[x][y]=\sum_{i=0}^{x-p} f[p][y-i]a^{x-p-i}b^iC_{x-p}^i$$
　　 $C_{x-p}^i$即为第i+1个数的系数。因为你可以视为从f[p][y-i]这个格子走到f[x][y]，而它们的行差为x-p；而它只有两种走法：1.往下走一格；2.往右下走一格。由于它们都得往下走，所以总共走了x-p步；而且由于行差为y-(y-i)=i，所以按照走法2走了i步。于是总共有 $C_{x-p}^i$种走法。
　　时间复杂度：预处理阶乘及逆元 $O(nlog_2998244353)$，计算答案 $O(qn)$。

Code

#include <cstdio>
#include <cctype>
#include <algorithm>
using namespace std;
#define MI 101
#define N MI*1000
#define M N*100
#define MO 998244353
#define ll long long
#define fo(i,a,b) for(i=a;i<=b;i++)
#define fd(i,a,b) for(i=a;i>=b;i--)
int i,j,m,n,p,q,x[MI],y[MI];
ll a,b,na,A[N],f[N][MI],jc[M],nj[M];
void read(int &x)
{
    char c=getchar(); x=0;
    for(;!isdigit(c);c=getchar());
    for(;isdigit(c);x=(x<<3)+(x<<1)+c-'0',c=getchar());
}
void read(ll &x)
{
    char c=getchar(); x=0;
    for(;!isdigit(c);c=getchar());
    for(;isdigit(c);x=(x<<3)+(x<<1)+c-'0',c=getchar());
}
ll ksm(ll x,int y)
{
    ll ans=1;
    while(y)
    {
        if(y&1)ans=ans*x%MO;
        x=x*x%MO;
        y>>=1;
    }
    return ans;
}
inline ll ny(ll x)
{
    return ksm(x,MO-2);
}
void scan()
{
    read(m);read(n);read(a);read(b);read(p);read(q);
    na=ny(a);
    fo(i,1,n)read(A[i]);
    fo(i,1,q)read(x[i]),read(y[i]);
}
void init1()
{
    fo(i,1,n)f[p][i]=A[i];
    fo(i,p+1,m)
    {
        f[i][1]=a*f[i-1][1]%MO;
        fo(j,2,n)f[i][j]=(a*f[i-1][j]+b*f[i-1][j-1])%MO;
    }
    fd(i,p-1,1)
    {
        f[i][1]=na*f[i+1][1]%MO;
        fo(j,2,n)f[i][j]=na*(f[i+1][j]-b*f[i][j-1]%MO+MO)%MO;
    }
}
void init2()
{
    jc[0]=nj[0]=1;
    ll i;
    fo(i,1,m)nj[i]=ny(jc[i]=jc[i-1]*i%MO);
}
inline ll C(int n,int m)
{
    return jc[m]*nj[n]%MO*nj[m-n]%MO;
}
void work()
{
    if(n<=MI&&m<=N)
    {
        init1();
        fo(i,1,q)printf("%lld\n",f[x[i]][y[i]]);
        return;
    }
    init2();
    int all,ac;
    ll xs,as,bs,ans;
    fo(i,1,q)
    {
        all=ac=x[i]-p;
        ans=0;
        fo(j,0,min(y[i]-1,all))
        {
            xs=C(j,all);
            as=ksm(a,ac);
            bs=ksm(b,j);
            ans=(ans+xs*as%MO*bs%MO*A[y[i]-j])%MO;
            ac--;
        }
        printf("%lld\n",ans);
    }
}
int main()
{
    freopen("table.in","r",stdin);
    freopen("table.out","w",stdout);
    scan();
    work();
}

100points

　　考虑对于x＜p的f[x][y]怎么求。
　　类似60points方法，我们可以视为f[p][i]对上方的数有两种贡献：1.往上走一步，则为$\frac{1}{a}f[p][i]$的贡献；2.往右走一步（必须先离开第p行），则为$-\frac{b}{a}f[p][i]$的贡献。
　　因此，对于x＜p，有：

$$f[x][y]=\sum_{i=1}^y \frac{f[p][i](-b)^{y-i}C_{p-x+y-i-1}^{p-x-1}}{a^{p-x+y-i}}$$
　　因为y-i为行差，所以它总共按照走法2走了y-i步，所以-b的指数为y-i；而p-x为行差，所以它总共走了p-x+y-i步，所以a的指数为-(p-x+y-i)。而它要先离开第p行才能按走法2走，所以其实相当于它从f[p-1][i]往上、往右走到f[x][y]的方案数；而这样一来，就总共要走p-x+y-i-1步，且要按照走法1走p-x-1步，于是系数就为 $C_{p-x+y-i-1}^{p-x-1}$。
　　从计算公式可以看出，我们必须要计算 $O(n+m)$级别的阶乘及其逆元以及a的次幂的逆元，而m最大为 $10^7$，用60points的预处理方法很慢。那么考虑优化它。
　　我们在计算a的次幂的逆元时，可以不必对每个次幂都计算它的-1次幂。因为我们可以先求出 $a^{-1}$，而且我们知道， $a^{-2}=a^{-1}·a^{-1}$， $a^{-x}=a^{-x+1}·a^{-1}$。但是阶乘的逆元就 凉拌炒鸡蛋了得用一种比较神奇的方法了：
　　我们知道，i!的逆元等于 $\frac{1}{i!}$。那么，设i!的逆元为nj[i]，则对于nj[i]其实可以用nj[i+1]转移过来：因为 $\frac{1}{(i+1)!}=\frac{1}{i!(i+1)}$，于是 $\frac{1}{i!}=\frac{i+1}{(i+1)!}$。所以，我们可以先求出nj[n+m]，再倒推一波，计算出nj[0~n+m-1]。
　　时间复杂度：预处理各种东西 $O(n+m+log_2998244353)$，计算答案 $O(qn)$。

Code

#include <cstdio>
#include <cctype>
#include <algorithm>
using namespace std;
#define MI 101
#define N MI*1000
#define M N*100
#define MO 998244353
#define ll long long
#define fo(i,a,b) for(i=a;i<=b;i++)
#define fd(i,a,b) for(i=a;i>=b;i--)
int i,j,m,n,p,q;
ll a,b,x,y,na,A[N],jc[M+N],nj[M+N],MA[M+N],NA[M+N],MB[M+N];
void read(int &x)
{
    char c=getchar(); x=0;
    for(;!isdigit(c);c=getchar());
    for(;isdigit(c);x=(x<<3)+(x<<1)+c-'0',c=getchar());
}
void read(ll &x)
{
    char c=getchar(); x=0;
    for(;!isdigit(c);c=getchar());
    for(;isdigit(c);x=(x<<3)+(x<<1)+c-'0',c=getchar());
}
ll ksm(ll x,int y)
{
    ll ans=1;
    while(y)
    {
        if(y&1)ans=ans*x%MO;
        x=x*x%MO;
        y>>=1;
    }
    return ans;
}
inline ll ny(ll x)
{
    return ksm(x,MO-2);
}
void scan()
{
    read(m);read(n);read(a);read(b);read(p);read(q);
    na=ny(a);
    fo(i,1,n)read(A[i]);
}
void init()
{
    jc[0]=MA[0]=NA[0]=MB[0]=1;
    ll i;
    fo(i,1,m+n)
    {
        jc[i]=jc[i-1]*i%MO;
        MA[i]=MA[i-1]*a%MO;
        NA[i]=NA[i-1]*na%MO;
        MB[i]=MB[i-1]*b%MO;
    }
    nj[m+n]=ny(jc[m+n]);
    fd(i,m+n-1,0)nj[i]=nj[i+1]*(i+1)%MO;
}
inline ll C(int m,int n)
{
    return jc[m]*nj[n]%MO*nj[m-n]%MO;
}
void work()
{
    init();
    int all,hc,lc,ac;
    ll xs,as,bs,ans;
    fo(i,1,q)
    {
        read(x);read(y);
        ans=0;
        if(x>=p)
        {
            as=MA[all=ac=x-p];
            fo(j,0,min((ll)all,y-1))
            {
                xs=C(all,j);
                bs=MB[j];
                ans=(ans+xs*as%MO*bs%MO*A[y-j])%MO;
                as=MA[--ac];
            }
        }
        else
        {
            hc=p-x;
            fo(j,1,y)
            {
                lc=y-j;
                xs=C(hc+lc-1,hc-1);
                as=NA[hc+lc];
                bs=MB[lc];
                if((y-j)&1)bs=MO-bs;
                ans=(ans+xs*as%MO*bs%MO*A[j])%MO;
            }
        }
        printf("%lld\n",ans);
    }
}
int main()
{
    freopen("table.in","r",stdin);
    freopen("table.out","w",stdout);
    scan();
    work();
}