[Luogu P4769] [BZOJ 5416] [UOJ #394] [LOJ 2719] [NOI2018]冒泡排序

题目描述

最近，小S 对冒泡排序产生了浓厚的兴趣。为了问题简单，小 S 只研究对 $1$ 到 $n$ 的排列的冒泡排序。

下面是对冒泡排序的算法描述。

输入：一个长度为 $n$ 的排列 $p[1...n]$

输出： $p$ 排序后的结果。

for i = 1 to n do
    for j = 1 to n - 1 do
        if(p[j] > p[j + 1])
            交换p[j] 与p[j + 1] 的值

冒泡排序的交换次数被定义为交换过程的执行次数。可以证明交换次数的一个下界是 $\frac{1}{2} \sum_{i=1}^n |i-p_i|$ 其中 $p_i$ 是排列 $p$ 中第 $i$ 个位置的数字。如果你对证明感兴趣，可以看提示。

小S 开始专注于研究长度为 $n$ 的排列中，满足交换次数 $= \frac{1}{2} \sum_{i=1}^n |i-p_i|$ 的排列（在后文中，为了方便，我们把所有这样的排列叫“好”的排列）。他进一步想，这样的排列到底多不多？它们分布的密不密集？小S 想要对于一个给定的长度为 $n$ 的排列 $q$ ，计算字典序严格大于 $q$ 的“好”的排列个数。但是他不会做，于是求助于你，希望你帮他解决这个问题，考虑到答案可能会很大，因此只需输出答案对 $998244353$ 取模的结果。

输入输出格式

输入格式：

从文件inverse.in 中读入数据。

输入第一行包含一个正整数T，表示数据组数。

对于每组数据，第一行有一个正整数 $n$ , 保证 $n \leq 6 \times 10^5$ 。

接下来一行会输入 $n$ 个正整数，对应于题目描述中的 $q_i$ ，保证输入的是一个 $1$ 到 $n$ 的排列。

输出格式：

输出到文件inverse.out 中。

输出共 $T$ 行，每行一个整数。

对于每组数据，输出一个整数，表示字典序严格大于 $q$ 的“好”的排列个数对 $998244353$ 取模的结果。

输入输出样例

输入样例#1：

1
3
1 3 2

输出样例#1：

输入样例#2：

1
4
1 4 2 3

输出样例#2：

说明

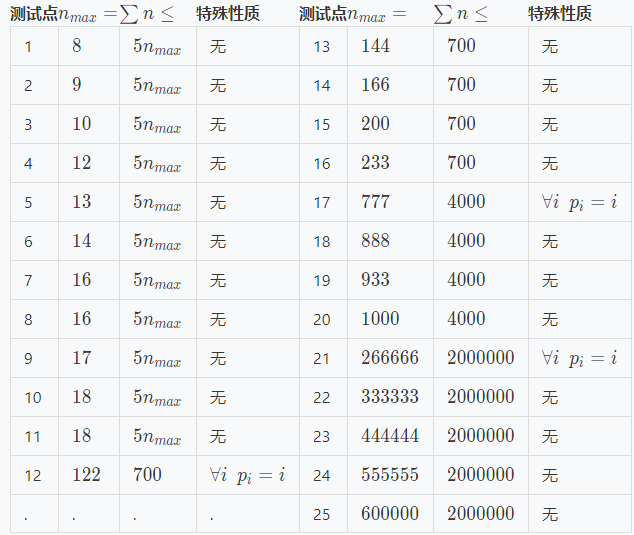
下面是对本题每个测试点的输入规模的说明。

对于所有数据，均满足 $T = 5$ (样例可能不满足).
记 $n_{max}$ 表示每组数据中 $n$ 的最大值，
$\sum n$ 表示所有数据的 $n$ 的和。

下面是对交换次数下界是 $\frac{1}{2} \sum_{i=1}^n |i-p_i|$ 的证明。

排序本质上就是数字的移动，因此排序的交换次数应当可以用数字移动的总距离来描述。对于第 $i$ 个位置，假设在初始排列中，这个位置上的数字是 $p_i$ ，那么我们需要将这个数字移动到第 $p_i$ 个位置上，移动的距离是 $|i-p_i|$ 。从而移动的总距离就是 $\sum_{i=1}^n |i-p_i|$ ，而冒泡排序每次会交换两个相邻的数字，每次交换可以使移动的总距离至多减少 $2$ 。因此 $\frac{1}{2} \sum_{i=1}^n |i-p_i|$ 是冒泡排序的交换次数的下界。

并不是所有的排列都达到了下界，比如在 $n = 3$ 的时候，考虑排列 $3\ 2\ 1$ , 这个排列进行冒泡排序以后的交换次数是 $3$ ，但是 $\frac{1}{2} \sum_{i=1}^n |i-p_i|$ 只有 $2$ 。

【样例1 解释】字典序比 $1\ 3\ 2$ 大的排列中，除了 $3\ 2\ 1$ 以外都是“好”的排列，故答案为 $3$ 。

解题分析

证明已经基本上告诉我们了，如果可以达到下界，那么最长下降子序列的长度不能超过 $2$ ，否则由于要交换最小最大的两个元素中间的那个元素会多交换，无法达到最优。

那么设 $dp[i][j]$ 表示已选 $i$ 个数放入序列，其中最大值为 $j$ 的方案数，如果下一个可选的数比 $j$ 大，显然是合法的。但如果下一个数比 $j$ 小，为了保证最长下降子序列的长度不超过 $2$ ，显然应该选当前未选的元素中最小的一个，因此这个转移是唯一的。所以 $dp[i][j]$ 可转移至 $dp[i+1][j+k](j+k\le n,k\ge 0)$ 。

把 $(i,j)$ 视为一个点，那么发现实际上我们要求的就是 $(0,0)$ 到 $(n,n)$ 且不跨过 $y=x$ 这条直线，始终保持在其上方的，只能向右或向右上走的方案数。这实际上就是 $Catalan(n)$ 。

那么如果加上字典序限制怎么办呢？类似数位 $dp$ ，我们可以先算一部分最高位比限制大的方案数，这样之后的数位是不会受到影响的，然后假设这位恰好为当前位限制的大小继续推下一位。

例如下面这个例子：

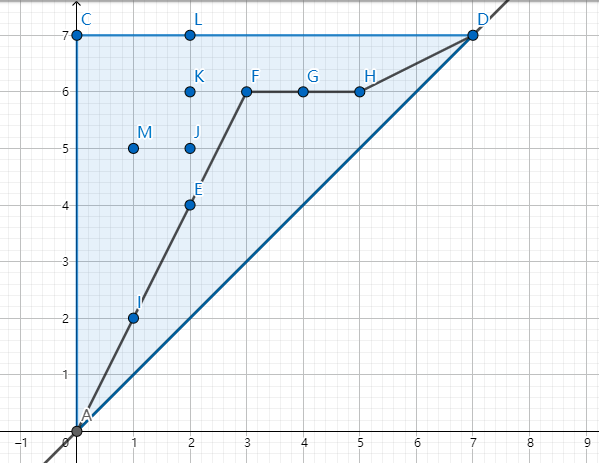
假设我们现在在考虑 $E$ 先的限制，那么其上面的三个点都不受后面字典序的限制。我们只需要求出这三个点只向右或向右上走到 $D$ 点，且不跨过 $y=x$ 这条直线的方案数。显然这个值也就等于 $M$ 点到 $D$ 点的方案数。

这个方案数怎么算？就是这道题…预处理逆元，阶乘即可 $O(1)$ 计算。

另外，注意如果我们强制卡满限制，填数也是需要满足上面我们 $dp$ 的要求的，如果某次填入的限制比当前最大的限制小，且不是最小的一个未填的元素，直接 $break$ 即可，因为这样根本不能满足要求，一定会在这一位选取到一个更大的数。

代码如下：

#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cctype>
#include <cstring>
#include <algorithm>
#define R register
#define IN inline
#define W while
#define gc getchar()
#define MX 1205000
#define MOD 998244353ll
#define ll long long
template <class T>
IN void in(T &x)
{
	x = 0; R char c = gc;
	for (; !isdigit(c); c = gc);
	for (;  isdigit(c); c = gc)
	x = (x << 1) + (x << 3) + c - 48;
}
template <class T> IN T max(T a, T b) {return a > b ? a : b;}
int fac[MX], inv[MX], bd[MX];
bool used[MX];
IN void pre()
{
	fac[0] = fac[1] = inv[0] = inv[1] = 1;
	for (R int i = 2; i <= 1200000; ++i)
	{
		fac[i] = 1ll * fac[i - 1] * i % MOD;
		inv[i] = 1ll * inv[MOD % i] * (MOD - MOD / i) % MOD;
	}
	for (R int i = 2; i <= 1200000; ++i) inv[i] = 1ll * inv[i] * inv[i - 1] % MOD;
}
IN int C(R int n, R int m)
{
	if (n < m) return 0;
	return 1ll * fac[n] * inv[m] % MOD * inv[n - m] % MOD;
}
int main(void)
{
	int T, n, lim, mn, mx, ans; pre(), in(T);
	W (T--)
	{
		in(n); mx = ans = 0, mn = 1;
		std::memset(used, false, sizeof(bool) * (n + 1));
		for (R int i = 1; i <= n; ++i) in(bd[i]);
		for (R int i = 1; i <= n; ++i)
		{
			lim = max(mx + 1, bd[i] + 1); used[bd[i]] = true;
			if (lim <= n)
			(ans += ((C(2 * n - i - lim + 1, n - i + 1) - C(2 * n - i - lim + 1, n - i + 2) + MOD) % MOD)) %= MOD;
			if (mx < bd[i]) mx = bd[i];
			else if (bd[i] != mn) break;
			W (used[mn]) ++mn;
		}
		printf("%d\n", ans);
	}
}