在之前我们有介绍过贝叶斯线性回归,贝叶斯线性回归利用了最大后验估计(MAP)加上权重的高斯分布先验推导出带有L2正则项的线性回归。
其实这就是岭回归,即 岭回归=MAP+高斯先验。
推导就参见贝叶斯线性回归了,其实两者就是一模一样的东西,不过贝叶斯线性回归更侧重于推导这个过程,因为用了MAP方法,而提到岭回归我们就会更去研究强调其L2正则项的一些特性与作用。
直接给出岭回归的推导结果:
强烈建议阅读其MAP+高斯分布先验的推导过程
Normal Equation推导
接下来就按照之前在线性回归之Normal Equation里讲过的Normal Equation方法推导一下加入L2正则化之后的岭回归有什么不同。
对上面的目标函数做一些符号替换以及变形,我们记,
,
,
则得到新的目标函数:
向量化变形之后得到:

对其求导得:
最后可以得到:
我们记(后面会用到)
可以发现上述正规方程与一般线性回归的正规方程相比,多了一项,其中
表示单位矩阵。假如
是一个奇异矩阵(不满秩),添加这一项后可以保证该项可逆。由于单位矩阵的形状是对角线上为1其他地方都为0,看起来像一条山岭,因此而得名。
回顾一下,Normal Equation方法可以帮助我们求解得到误差最小的向量,至于为什么加入
之后可以解决矩阵病态等问题,会在之后新开一篇文章来详细讲解。先稍微提一嘴,单位矩阵
是满秩矩阵,故
也是满秩矩阵,所以可以求稳定的逆。
岭回归的几何解释
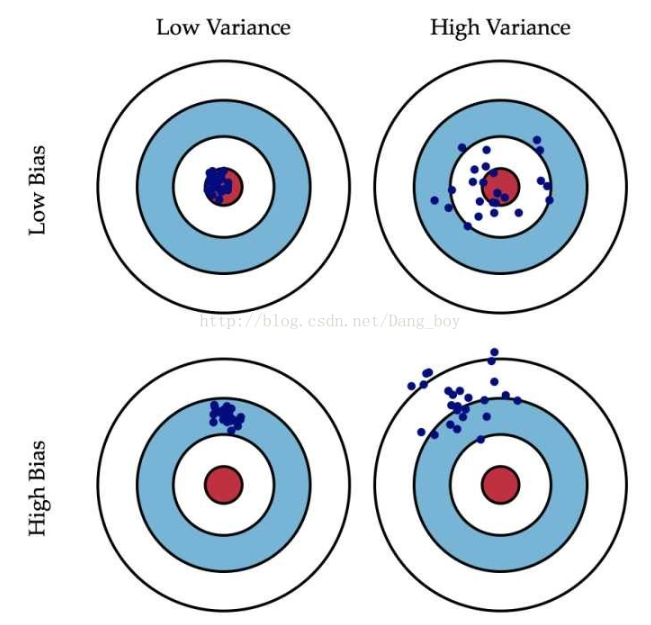
先来回顾一下偏差与方差:
偏差:预测数据和真实数据的差距
方差:预测出来数据的分散程度
下面以两变量为例
没有约束项时系数β1和β2已经经过标准化。残差平方和RSS可以表示为β1和β2的一个二次函数,数学上可以用一个抛物面表示。

约束项对应着投影为β1和β2平面上的一个圆,即下图中的圆柱

椭圆形抛物面为即平方差损失函数,圆柱形为
,由最小二乘法求得的解释抛物面的最低点,由岭回归得到的是黄色的点,一般来说,拟合的误差值(偏差)越小,
的各个元素(权值)的方差越高,所以岭回归是找到一个方差不会太大,误差也不会太大的权衡的点。随着t的增大,也就是圆柱的半径,方差变大(对照上面偏差方差的图仔细想一下)。
从β1,β2平面理解,即为抛物面等高线在水平面的投影和圆的交点,如下图所示

这幅图其实在之前讲L1、L2正则化时出现过。
岭回归的性质:
- 当岭参数为0,得到最小二乘解。
- 当岭参数λ趋向更大时,岭回归系数A估计趋向于0。
- 岭回归是回归参数A的有偏估计。它的结果是使得残差平和变大,但是会使系数检验变好。
- 在认为岭参数λ是与y无关的常数时,是最小二乘估计的一个线性变换,也是y的线性函数。
- 但在实际应用中,由于λ总是要通过数据确定,因此λ也依赖于y、因此从本质上说,并非的线性变换,也非y的线性函数。
- 对于回归系数向量来说,有偏估计回归系数向量长度<无偏估计回归系数向量长度。即
。
- 存在某一个λ,使得它所对应的的MSE(估计向量的均方误差)<最小二乘法对应估计向量的的MSE。即 存在λ>0,使得
岭迹图:
是的函数,岭迹图的横坐标为
,纵坐标为
。而
是一个向量,由
、
、…等很多分量组成,每一个分量都是
的函数,将每一个分量分别用一条线。
当不存在奇异性时,岭迹应是稳定地逐渐趋向于0
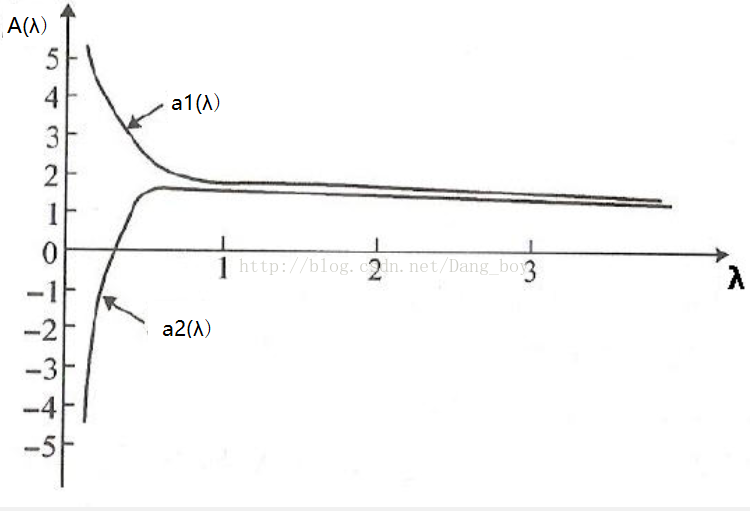
其实很好理解,当趋向于无穷的时候,所有参数都应该趋向于0,惩罚很大。
岭迹图作用:
- 观察λ较佳取值;
- 观察变量是否有多重共线性;
在很小时,
很大,且不稳定,当
增大到一定程度时,
系数迅速缩小,趋于稳定。
的选择:一般通过观察,选取喇叭口附近的值,此时各
各分量已趋于稳定,但总的RSS又不是很大。
选择变量:删除那些取值一直趋于0的变量。
岭参数的一般选择原则
选择λ值,使得
- 各回归系数的岭估计基本稳定;
- 用最小二乘估计时符号不合理的回归系数,其岭估计的符号变得合理;
- 回归系数没有不合乎实际意义的值;
- 残差平方和增大不太多。 一般λ越大,系数β会出现稳定的假象,但是残差平方和也会更大。
取λ的方法比较多,但是结果差异较大。这是岭回归的弱点之一。
参考文章: