一、线性回归的形式
1.线性回归通过y=XW的形式来拟合p(y|X)的条件分布公式。X为每行一个样本的矩阵,W为参数列向量。也可用其他形式的函数(如多项式)来进行拟合。
2.问题是希望找到最优的W,使得均方误差最小化,即求得使(y-XW)^T*(y-XW)最小的W。问题等价于解上式对W求偏导等于0(此处为零向量,因为均方误差对W求导得到的是梯度向量)的W的解,即2X^T*(XW-y)(使用到了多维求导,W是向量,均方误差是标量。)
3.均方误差对应了欧式距离,最小二乘法就是试图在超空间中找到一个超平面,使所有样本到超平面的欧式距离之和最小。
4.从正态分布的角度来看,线性回归假设yi=XW+ei,e为服从(0,sigma)正态分布的噪音,且各ei独立同分布。则y服从(XW,sigma)的正态分布。由此,参数为W下的多元概率分布P(y|X)可写成正态分布的密度函数,对W进行极大似然估计,可推出与最小二乘相同的优化表达式。
二、多维求导
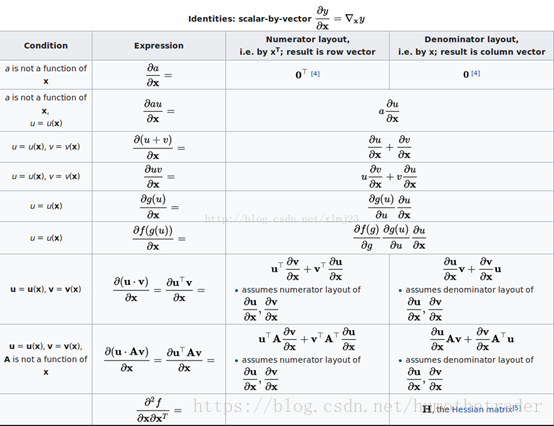
1.标量对向量求导,结果是与向量相同维度的梯度向量。
Hessian矩阵为标量对向量的求二次导组成的,第一列为因变量对x1到xn求导后再对x1求导,第二列为对各x求导后再对x2求导。在二阶偏导连续的点,对两个变量求偏导的顺序在交换后值不变,所以Hessian矩阵在大多数函数几乎处处对称。当Hessian矩阵时实对称的,我们可以将其进行特征分解,而各方向上的二阶倒数是H的所有特征值的加权(权重0到1)。当H是正定的,该临界点是局部极小点。负定,局部极大点。有正有负则为鞍点。当所有非零特征值同号且有一个特征值为0,二阶测试不确定。
2.向量对向量求导,得Jacobian矩阵,每行不同的y,每列不同的x,列成求导表。这个矩阵的第i行是由梯度函数的转置yi(i=1,…,m)表示的。
3.矩阵对向量求导,得到的矩阵与矩阵相同维度,第n列为矩阵第n列除向量第n个元素。

4.标量对矩阵求导,得到梯度矩阵,大小与矩阵相同。
计算技巧:
三、求解偏导为0的函数
1.2X^T(XW-y)=0向量求解,变换为W=(X^T*X)^-1 *X^T*y(该式称为正规方程)。直观来看,可以直接求出W,但X左乘X转置不一定能求逆。
2.X左乘X转置得到一个矩阵,行数列数均为数据集的特征数,第一列是特征向量1分别点积其他各向量,第二列是特征向量2分别点积,以此类推。(1)若特征之间存在线性关系,则现在的矩阵各列之间也会存在对应的线性关系,则该矩阵不满秩。(2)若特征数多于样本数,则该矩阵不满秩。
3.矩阵不满秩的解决方案:将式子改为W=(X^T*X+lambda*I)^-1 *X^T*y。由于加上的对角阵一定正定,加在X左乘X转置上后该矩阵也正定,正定则没有特征值为零,矩阵一定可逆。该方案等同于在最小二乘后面加L2正则项后解出来的正规方程,lambda越大则对参数空间的限制越死。加上的内容被称为扰动。加入
4.梯度下降:特征多时,建议使用梯度下降来解决该问题。在梯度下降中,cost function可以加入l2正则化项和l1正则化项,l2正则化加入后仍可以使用梯度下降求解,或像上面那样使用正规方程,称为Ridge(岭)回归。l1加入后不可用上述方法求解,因为加入后损失函数对w在零点处不可导。
5.l1正则化对应于假设W的先验服从拉普拉斯分布的先验,l2正则化对应于假设W的先验服从正态分布的先验。l1和l2都能防止过拟合,但l1能产生更稀疏的模型,有利于模型的存储,也能够用于特征选择(降维),这是由于l1用以坐标轴为对角线的方形区域来限制各参数,lambda越大该区域越小,则可行区域存在许多边啊面啊,在这些边、面上许多参数等于0,这种限制形状使得参数取到这些区域的概率更高。而l2正则化使用的是圆形区域去限制参数,l2正则化在梯度下降中对应于每次梯度更新前让参数乘以一个小于1的系数,这使得参数在不考虑梯度更新的情况下有越来越小的趋势。
6.加入l1正则化后使用坐标下降法求解(lasso回归)。坐标下降法:随机初始化一组参数,随机或顺序抽取一个维度的参数,固定其他参数为常数的情况下求解该参数的最小值,收敛后换一个维度,直到所有维度的更新都小于阈值为止。
7.其他正则化方式有:增大数据集(或数据集增强),或随机失活(神经网络中使用)。