简介
卡特兰数又称卡塔兰数,英文名Catalan number,是组合数学中一个常出现在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名,其前几项为(从第零项开始) : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...


其通项公式为:
- 通项公式:h(n)=C(n,2n)/(n+1)=(2n)!/((n!)*(n+1)!) = C(n, 2n) - C(n +1, 2n)
- 递推公式1:h(n)=((4*n-2)/(n+1))*h(n-1);
- 递推公式2:h(n)=h(0)*h(n-1)+h(1)*h(n-2)+...+h(n-1)*h(0).
- 其前几项为:h(0)=1,h(1)=1,h(2)=2,h(3)=5,h(4)=14,h(5)=42,......
分析与应用
参考自:http://buptdtt.blog.51cto.com/2369962/832586
分析:
- 一个经典的例子:对于给定的n个左括号和右括号,现在问有多少序列使得所有的括号都可以匹配(即有匹配的括号就删去,一直重复) 这个问题的另一种表述就是,现在有两类物品各n个,线型排列,对于每一个位置,从左侧第一个到当前位置:A类物品的数量>=B类物品的数量,问序列个数
- 思路:考虑最后一个位置,这时候Na==Nb。那我们考虑一下子问题,序列中必然存在一个分割,使得左边和右边都是这个问题的子问题(Na==Nb)。但是,如果把左右这两个都当做子问题,那么将在分割的时候会导致重复(比如n=6,左2右4和左4右2重复)。所以,我们需要将左右的状态区分开。显然,左边的最左边一定是A物体,最右边一定是B物体,那么中间的x-2个依然是子问题,但是对于左右两侧的问题我们已经保证了不会重复(对于左边的状态,除去最后一个点,那么均保证了A类物品的数量>B类物品的数量)。
- 总结:
卡特兰书分析的关键:找到子问题(形式要和递推式类似)、保证子问题不重复
应用:
- 矩阵链乘: P=a1×a2×a3×……×an,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?
思路:可以这样考虑,首先通过括号化,将P分成两个部分,然后分别对两个部分进行括号化。比如分成(a1)×(a2×a3.....×an),然后再对(a1)和(a2×a3.....×an)分别括号化;又如分成(a1×a2)×(a3.....×an),然后再对(a1×a2)和(a3.....×an)括号化。
设n个矩阵的括号化方案的种数为f(n),那么问题的解为
f(n) = f(1)*f(n-1) + f(2)*f(n-2) + f(3)*f(n-3) + f(n-1)*f(1)。f(1)*f(n-1)表示分成(a1)×(a2×a3.....×an)两部分,然后分别括号化。
计算开始几项,f(1) = 1, f(2) = 1, f(3) = 2, f(4) = 5。结合递归式,不难发现f(n)等于h(n-1)。 - 一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列?
思路:这个与加括号的很相似,进栈操作相当于是左括号,而出栈操作相当于右括号。n个数的进栈次序和出栈次序构成了一个含2n个数字的序列。第0个数字肯定是进栈的数,这个数相应的出栈的数一定是第2i+1个数。因为如果是2i,那么中间包含了奇数个数,这奇数个肯定无法构成进栈出栈序列。
设问题的解为f(2n), 那么f(2n) = f(0)*f(2n-2) + f(2)*f(2n-4) + f(2n-2)*f(0)。f(0) * f(2n-2)表示第0个数字进栈后立即出栈,此时这个数字的进栈与出栈间包含的数字个数为0,剩余为2n-2个数。f(2)*f(2n-4)表示第0个数字进栈与出栈间包含了2个数字,相当于1 2 2 1,剩余为2n-4个数字。依次类推。
假设f(0) = 1,计算一下开始几项,f(2) = 1, f(4) = 2, f(6) = 5。结合递归式,不难发现f(2n) 等于h(n)。 - n个节点构成的二叉树,共有多少种情形?
思路:可以这样考虑,根肯定会占用一个结点,那么剩余的n-1个结点可以有如下的分配方式,T(0, n-1),T(1, n-2),...T(n-1, 0),设T(i, j)表示根的左子树含i个结点,右子树含j个结点。
设问题的解为f(n),那么f(n) = f(0)*f(n-1) + f(1)*f(n-2) + .......+ f(n-2)*f(1) + f(n-1)*f(0)。假设f(0) = 1,那么f(1) = 1, f(2) = 2, f(3) = 5。结合递推式,不难发现f(n)等于h(n)。 - n对括号有多少种匹配方式?
思路:n对括号相当于有2n个符号,n个左括号、n个右括号,可以设问题的解为f(2n)。第0个符号肯定为左括号,与之匹配的右括号必须为第2i+1字符。因为如果是第2i个字符,那么第0个字符与第2i个字符间包含奇数个字符,而奇数个字符是无法构成匹配的。
通过简单分析,f(2n)可以转化如下的递推式 f(2n) = f(0)*f(2n-2) + f(2)*f(2n - 4) + ... + f(2n - 4)*f(2) + f(2n-2)*f(0)。简单解释一下,f(0) * f(2n-2)表示第0个字符与第1个字符匹配,同时剩余字符分成两个部分,一部分为0个字符,另一部分为2n-2个字符,然后对这两部分求解。 f(2)*f(2n-4)表示第0个字符与第3个字符匹配,同时剩余字符分成两个部分,一部分为2个字符,另一部分为2n-4个字符。依次类推。
假设f(0) = 1,计算一下开始几项,f(2) = 1, f(4) = 2, f(6) = 5。结合递归式,不难发现f(2n) 等于h(n)。 - 在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
思路:以其中一个点为基点,编号为0,然后按顺时针方向将其他点依次编号。那么与编号为0相连点的编号一定是奇数,否则,这两个编号间含有奇数个点,势必会有个点被孤立,即在一条线段的两侧分别有一个孤立点,从而导致两线段相交。设选中的基点为A,与它连接的点为B,那么A和B将所有点分成两个部分,一部分位于A、B的左边,另一部分位于A、B的右边。然后分别对这两部分求解即可。
设问题的解f(n),那么f(n) = f(0)*f(n-2) + f(2)*f(n-4) + f(4)*f(n-6) + ......f(n-4)*f(2) + f(n-2)*f(0)。f(0)*f(n-2)表示编号0的点与编号1的点相连,此时位于它们右边的点的个数为0,而位于它们左边的点为2n-2。依次类推。
f(0) = 1, f(2) = 1, f(4) = 2。结合递归式,不难发现f(2n) 等于h(n)。 - 求一个凸多边形区域划分成三角形区域的方法数?
思路:以凸多边形的一边为基,设这条边的2个顶点为A和B。从剩余顶点中选1个,可以将凸多边形分成三个部分,中间是一个三角形,左右两边分别是两个凸多边形,然后求解左右两个凸多边形。
设问题的解f(n),其中n表示顶点数,那么f(n) = f(2)*f(n-1) + f(3)*f(n-2) + ......f(n-2)*f(3) + f(n-1)*f(2)。f(2)*f(n-1)表示三个相邻的顶点构成一个三角形,那么另外两个部分的顶点数分别为2和n-1。
设f(2) = 1,那么f(3) = 1, f(4) = 2, f(5) = 5。结合递推式,不难发现f(n) 等于h(n-2)。 - 描述:有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?
思路:可以将持5元买票视为进栈,那么持10元买票视为5元的出栈。这个问题就转化成了栈的出栈次序数。由应用三的分析直接得到结果,f(2n) 等于h(n)*n!*n!。 - 拥有 n+1 个叶子节点的二叉树的数量为h(n).例如 4个叶子节点的所有二叉树形态:
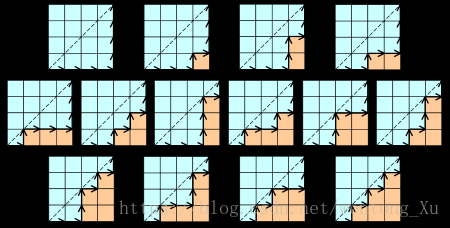
- n*n的方格地图中,从一个角到另外一个角,不跨越对角线的路径数为h(n).例如, 4×4方格地图中的路径有:
- 圆桌周围有 2n个人,他们两两握手,但没有交叉的方案数为h(n)
- 说16个人按顺序去买烧饼,其中8个人每人身上只有一张5块钱,另外8个人每人身上只有一张10块钱。烧饼5块一个,开始时烧饼店老板身上没有钱。16个顾客互相不通气,每人只买一个。问这16个人共有多少种排列方法能避免找不开钱的情况出现。h(8)=1430,所以总数=1430*8!*8!
-
在图书馆一共6个人在排队,3个还《面试宝典》一书,3个在借《面试宝典》一书,图书馆此时没有了面试宝典了,求他们排队的总数?
h(3)=5;所以总数为5*3!*3!=180.
有关例题:
hdoj 1134
2n个人围成一个圆圈,求两两相互握手并且不交叉的所有握手方式。
这个是卡特兰数的一个例子,设2n个人一共有h(n)种,那么现在第一个人可以和第2,4,6,。。。,2(n-1),2n,即必须保证和他握手的那个人两边是偶数,即为:
h(n)=h(0)*h(n-1)+h(1)*h(n-2)+...+h(n-1)*h0=(4*n-2)/(n+1) *h(n-1),h(0)=1,h(1)=1.
通项公式:h(n)=C(n,2n)/n+1=(2n)!/((n!)*(n+1)!)
但是这个题目是大数,所以必须采用数组模拟乘除法.
#include <iostream>
#include <stdio.h>
using namespace std;
const int N=105;
int catalan[102][N];
void setCatalan()
{
memset(catalan,0,sizeof(catalan));
catalan[1][0]=1;
int i,tmp[N],j,yushu,m;
for(i=2;i<=100;i++)
{
m=4*i-2;
//大数乘法
for(j=0;j<N;j++)
{
catalan[i][j]+=catalan[i-1][j]*m;
if(catalan[i][j]>=10)
{
catalan[i][j+1]+=catalan[i][j]/10;
catalan[i][j]=catalan[i][j]%10;
}
}
for(j=0;j<N;j++)
tmp[j]=0;
yushu=0;
m=i+1;
//大数/小数
for(j=N-1;j>=0;--j)
{
tmp[j]=(10*yushu+catalan[i][j])/m;
yushu=(10*yushu+catalan[i][j])%m;
}
for(j=0;j<N;++j)
catalan[i][j]=tmp[j];
}
}
int main()
{
setCatalan();
int i,n;
while(cin>>n && (-1 != n))
{
i=N-1;
while(!catalan[n][i])
--i;
for(;i>=0;--i)
cout<<catalan[n][i];
cout<<endl;
}
return 0;
}hdoj1023
求出栈序列,比如1,2,3,出栈序列为3 2 1,1 2 3,1 3 2,2 1 3,2 3 1,一共5种
我们把入栈看做1,出栈看做0,那么入栈出栈看做一系列的1010。。。,但是必须保证从左往右
看的时候1必须多余0,这个是卡塔兰数的第二个应用,种数为:C(n,2n)-C(n+1,2n).
粗略这样理解:我们从2n个位置中选出n个来存放1,方法数为C(n,2n),减去不满足的情况。
不合法的情况:我们在2n个位置放n+1个0,n-1个1,由于0的个数多2个,2n为偶数,故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换,使之成为由n个0和n个1组成的2n位数,即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数,即C(n+1,2n)。
h(n)=C(n,2n)-C(n+1,2n).
hdoj1130
给出n个点,求组成二叉树的所有种数,2个点组成2种二叉树,3个点组成5种二叉树。。。
这个也是卡塔兰数的一个应用,和1134类似,我们去除一个点作为根节点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) + + h(n-1)h(0)=h(n))。
hdoj2067
给出一个棋盘n*n,求从左下角到右上角的不经过对角线的所有走法,这个经过分析也是卡特兰数。我们把往右走看做1,把往上走看做0,那么从左向右看做一系列的101100.。。,和那个求出栈序列的就是一个问题了,即0的个数不能超过1,由于上半角和下半角一样,所以求出来卡特兰数*2就是我们的答案了。
hdoj1133
买票问题:有m个人手里拿的是50元的,n个人拿的是100元的,问使买票过程不中断的排队方式。我们知道如果前面出现拿50的人小于拿100的人,那么肯定出现找不开的情况,我们把拿50的看做0,拿100的看做1,所以从左往右看的时候0的个数必须大于1。我们知道总的情况为
C(n,m+n),需要求出不合法的序列个数,还是之前的思路,存在一个奇数位置2*k+1,使得0出现k此1出现k+1次,后面会有(m-k)个0,(n-k-1)个1,我们将01交换,即这个序列共有m+1个1,n-1个0,这个序列的所有排序情况就对应了一种不合法的序列情况(可以这样理解:由于m+1>n-1,那么必然在某一个位置出现1的个数大于0的个数,这样在这个位置往后的01我们交换回来,就对于了一种不合法的序列了),即C(m+1,m+n),最后的结果为:ans=C(n,m+n)-C(m+1,m+n),其中(m>=n);当m<n时买票过程必然中断。
#include <iostream>
using namespace std;
const int MAX=400;
const int BASE=1000;
int catalan[MAX],tmp[MAX];
int main()
{
int i,j,n,m,cas=0;
while(cin>>m>>n)
{
if(!(m+n))
break;
if(m<n)
printf("Test #%d:\n0\n",++cas);
else
{
memset(catalan,0,sizeof(catalan));
memset(tmp,0,sizeof(tmp));
catalan[0]=1;
//(m+n)!
for(i=1;i<=(m+n);++i)
{
for(j=0;j<MAX;j++)
catalan[j]=catalan[j]*i;
for(j=0;j<MAX;j++)
{
if(catalan[j]>=BASE)
{
catalan[j+1]+=catalan[j]/BASE;
catalan[j]=catalan[j]%BASE;
}
}
}
//*(m-n+1)
int k=m-n+1;
for(j=0;j<MAX;j++)
catalan[j]=catalan[j]*k;
for(j=0;j<MAX;j++)
{
if(catalan[j]>=BASE)
{
catalan[j+1]+=catalan[j]/BASE;
catalan[j]=catalan[j]%BASE;
}
}
// /(m+1)
int yushu=0;
k=m+1;
for(j=MAX-1;j>=0;--j)
{
tmp[j]=(BASE*yushu+catalan[j])/k;
yushu=(BASE*yushu+catalan[j])%k;
}
printf("Test #%d:\n",++cas);
j=MAX-1;
while(!tmp[j])
--j;
// cout<<"j"<<j<<endl;
printf("%d",tmp[j]);
--j;
for(;j>=0;--j)
printf("%03d",tmp[j]);
printf("\n");
}
}
return 0;
}例题参考自:http://www.cnblogs.com/buptLizer/archive/2011/10/23/2222027.html
感谢各位大神!