斯坦福大学机器学习笔记——单变量的线性回归以及损失函数和梯度下降法（包含代码）

回归问题：
所谓的回归问题就是给定的数据集，且每个数据集中的每个样例都有其正确的答案，通过给定的数据集进行拟合，找到一条能够最好代表该数据集的曲线，然后对于给定的一个样本，能够预测出该样本的答案（对于回归问题来说，最终的输出结果是一个连续的数值）。比如，房价预测问题，最终的输出房价是一个连续的数值。回归问题是监督学习的一种。
分类问题：
与回归问题一样，分类问题同属于监督学习，与之不同的是，分类问题预测的结果输出是离散的值，比如判断一个人得的肿瘤是良性的还是恶性的，这就是0/1离散输出问题。
对于一个回归问题来说，它的一般流程为：

其中，h代表拟合的曲线，也称为学习算法的解决方案或函数或假设。
单变量的线性回归是回归问题的一种，它的表达式为：
$h_{\theta }(x)=\theta _{0}+\theta _{1}x$
由于它只有一个特征/输入变量x，同时它拟合的曲线是一条直线，所以该问题叫做单变量线性回归问题。
以房价问题为例，来举例说明回归问题。

对于回归问题来说，假设的选择是一个关键问题，在只有数据的情况下，如何确定h的形式？我们假设房价问题是线性回归，则$\theta _{0}$和$\theta _{1}$，在房价问题这个例子中便是直线的斜率和在y轴上的截距。
但是我们如何选择参数$\theta _{0}$和$\theta _{1}$，来使得到的线性拟合更加准确呢！这里需要引入一个代价函数（cost function），该函数的功能就是衡量了预测的结果与真正结果之间的差距。
在回归问题中我们一般选择均方误差代价函数（也叫作平方误差代价函数），它是解决回归问题最常用的手段，该函数的表达形式如下：
$J(\theta _{0},\theta _{1})=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }(x^{i})-y^{i})^{2}$
训练的目标就是使得$J(\theta _{0},\theta _{1})$最小。
对于代价函数的理解可以通过下面一个例子加深：
回归问题的整个过程即为：

为了方便绘图和理解，可以对上述问题进行简化，上述各个形式转化为：

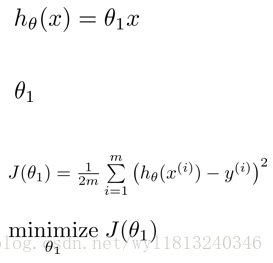
假设有三组数据，数据分别为（1，1），（2，2），（3，3）
当$\theta _{1}=0.5$时，$h_{\theta }(x)=0.5x$，这三个点分别预测为：
（1，0.5），（2，1），（3，1.5）
则此时的损失函数的值为(（1-0.5）^2+(1-2)^2+(3-1.5)^2)/(2*3)=0.583
当$\theta _{1}=1$时，$h_{\theta }(x)=x$这三个点分别预测为：
（1，1），（2，2），（3，3）
则此时的损失函数的值为（（1-1）^2+(2-2)^2+(3-3)^2）/(2*3)=0
以此类推，推出多个$\theta _{1}$值下的损失函数的值，然后绘制$\theta _{1}$和$J(\theta _{1})$的曲线，找到使得$J(\theta _{1})$取得最小值时的$\theta _{1}$的值。绘制的曲线为：

从中可以看出当$\theta _{1}=1$时损失函数最小，所以h的表达形式为：
$h_{\theta }(x)=x$
然后对于一个待测试的样本，最终的预测值就可以通过确定的h表达式来获得。这就是完整的回归问题。

上述的问题已经将其进行了简化，若不是简化形式，求解形式相同，只不过原来的$\theta _{1}$和$J(\theta _{1})$的曲线，转化为$\theta _{0}，\theta _{1}$和$J(\theta _{1}，\theta _{0})$曲面，代价函数的图形模样变成了下图所示：

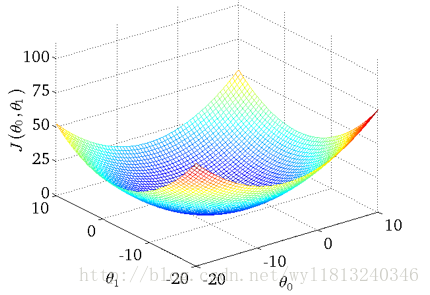
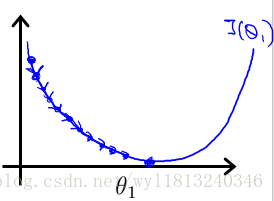
我们不希望通过上述方法，编个程序把这些点绘制出来，通过人工的方法将最低点找到。在低维的情况下还可以这么做，但是在高维更多参数的情况下，显然上述方法是不可行的。所以，可以使用梯度下降法来实现。

梯度下降法的思想是：开始随机选择一个参数的组合$（\theta _{0}，\theta _{1}，...,\theta _{n}）$，计算代价函数，然后我们寻找下一个能让代价函数下降最多的参数组合。我们持续这样做，直到到达一个局部最小值。由于我们没有尝试所有的参数组合，所以不能确定得到的结果是局部最小值还是全局最小值。
梯度下降法的数学定义如下：

其中，$\alpha$代表学习率（learning rate），它决定了沿着能让代价函数下降程度最大方向的步长。
值得注意的是，$\theta _{0}，\theta _{1}$是同时更新，也就是说：

如左图所示，为正确的更新过程，二者不同的地方在于，右图中在求$\theta _{1}$的更新时，代价函数中的$\theta _{0}$是已经更新过的了，而左图中的为将$\theta _{0}，\theta _{1}$都求过偏导之后再进行更新，代价函数中的$\theta _{0}，\theta _{1}$都是上一代中的值，与本次迭代更新无关。
下面举例说明梯度下降的过程：

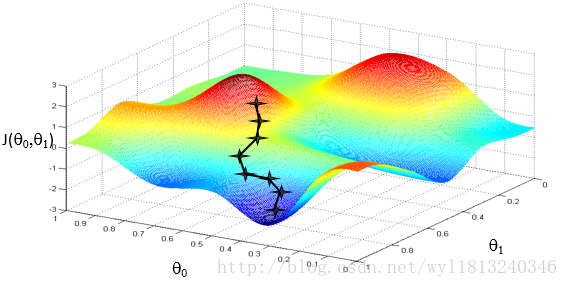
例如上图代表两座山，你现在所处的位置为最上面的那一点，你想以最快的速度达到山下，你环顾360度寻找能快速下山的方向，这个过程对应于求偏导的过程，你每次移动一步，移动的步长对应于$\alpha$，当你走完这一步，然后接着环顾360度，寻求最快下山的方法，然后在走出一步，重复这个过程，直到走到山下，走到山下对应于找到了局部最小值。

下面讨论一下步长$\alpha$和偏导对梯度下降法的影响：
注意：下图中讨论，都是在$\theta _{0}=0$的简单形式下讨论的。
步长对梯度下降法的影响：
1. 当步长太小时，每次走的步子很小，导致到达最小值的速度会很慢，也就是收敛速度慢，但是能保证收敛到最小值点。
2. 当步长太大时，梯度下降法可能会越过最小值点，甚至可能无法收敛。
两种情况的示意图如下：

梯度对梯度下降法的影响：
以下图为例：

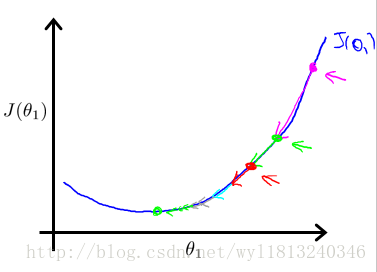
粉红色的点为初始点，在此点求出导数，然后乘以学习率，更新参数$\theta _{1}$，到达第二个点，然后再在第二个点求导数，从斜率上明显可以看出，第二个点的斜率明显比第一个点的斜率低，也就是说虽然学习率固定，但是这一次更新的步长比上一次要小，以此类推，我们能够得出一个结论，当接近局部最低时，导数值会自动变得越来越小，所以梯度下降法会自动采用较小的幅度，这就是梯度下降的做法。所以实际上没有必要再另外减小$\alpha$。

下面我们来讨论一下线性回归的梯度下降法：
梯度下降算法和线性回归算法如下图所示：

我们想用梯度下降算法来最小化损失函数，关键问题在于求导，即：

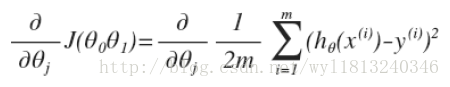
当j=0时：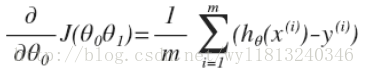
当j=1时：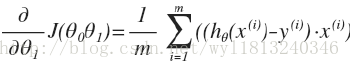
所以梯度下降算法修改为：

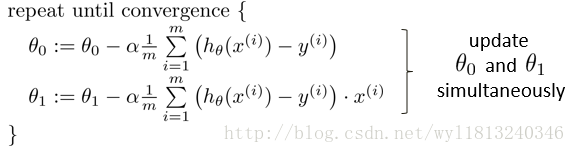
这就是线性回归的梯度下降法。有时候也称为批量梯度下降法，因为在梯度下降的每一步中，我们都用到了所有的训练样本。

使用matlab实现上述算法的代码如下：

clear;
close all;

%% 数据处理和初始化

data = load('ex1data1.txt'); % ex1data.txt中第一列是特征，第二列是标签
feature = data(:,1);    % 取出特征数据
result = data(:,2);  % 出标签数据

% 绘制数据分布，以确定使用哪种假设
figure(1);
plot(feature,result,'bo','MarkerSize', 3);   

m = length(result); % 计算样本的个数
feature = [ones(m,1) feature];  % 将特征进行扩展，在原来的基础上增加一列全为1的矩阵

% 初始化
theta = zeros(2,1); % 对theta进行初始化
iteration = 1500;  % 设置迭代次数
alpha = 0.02;    % 学习率

%% 训练模型和测试数据

% 训练模型，得到最优的theta值
[theta, all_theta, cost] = gradient_descent(theta, feature, result, iteration, alpha);

% 绘制随着迭代次数增加，损失函数的变化过程
x = 1:iteration;
y = cost;
figure;
plot(x',y);

% 测试数据
test_data = [15;8;5];   %测试数据
n = length(test_data);  %测试数据的个数  
test_data = [ones(n,1) test_data];  %测试数据的扩充
test_result = test_data * theta;    %测试数据的预测结果

%% 绘制决策边界

figure;
plot(feature(:,2),result,'bo','MarkerSize', 3);   %绘制数据分布
hold on;
plot(feature(:,2),feature*theta,'-');   %绘制决策边界
hold off;

%% 绘制损失函数曲线

% 观察theta1和theta2的取值范围，为后面选择theta1和theta2做准备
max_theta1=max(all_theta(1,:)); % theta1的最大值
min_theta1=min(all_theta(1,:)); % theta1的最小值
max_theta2=max(all_theta(2,:)); % theta2的最大值
min_theta2=min(all_theta(2,:)); % theta2的最小值

% % 产生101（数目无所谓）个theta1和theta2的值
% theta1 = -10:0.2:10;
% num_theta1 = length(theta1);
% theta2 = -2:3/50:4;
% num_theta2 = length(theta2);

% 一种更好的产生确定数目的方式
theta1 = linspace(-10, 10, 100); % 在-10~10范围内等间隔取100个数
num_theta1 = length(theta1);    % 确定theta1的数目
theta2 = linspace(-1, 4, 100);  % 在-1~4范围内等间隔取100个数
num_theta2 = length(theta2);    % 确定theta2的数目

% 计算上面的theta1和theta2对应下的损失函数
cost=zeros(num_theta1,num_theta2);
for i=1:num_theta1
    for j=1:num_theta2
        theta_temp = [theta1(i);theta2(j)];
        cost(i,j)=compute_cost(feature, result, theta_temp);
    end
end

surf(theta1, theta2, cost');    %由于meshgrid在surf命令中的工作方式，我们需要在调用surf之前需要将cost转置，否则坐标轴将被翻转
xlabel('\theta1');ylabel('\theta2');
title('cost function');

%% 绘制等高线图以及在等高线中找到损失函数取最小值得位置

figure;
contour(theta1, theta2, cost', logspace(-2, 3, 20))
xlabel('\theta_1'); ylabel('\theta_2');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);

上述代码中包含的函数为：

1.计算损失函数：

function cost = compute_cost(feature, result, theta)

m = length(result); % 样本的个数
cost = sum((feature*theta - result).^2)/(2*m);  % 计算当前theta下的损失

end

2.梯度下降算法：

function [theta, all_theta, cost] = gradient_descent(theta,feature,result,iteration,alpha)

[m,n] = size(feature);  % m代表样本的个数，m代表所需要参数的个数
cost = zeros(iteration,1); % 存储每次迭代的损失函数的值
all_theta = zeros(2, iteration);    % 存储所有theta值

for i=1:iteration

    cost(i) = compute_cost(feature, result, theta); % 计算损失函数
%     cost(i) = sum((feature*theta - result).^2)/(2*m);

    theta(1) = theta(1) - alpha * sum((feature * theta - result) .*feature(:,1)) / m;   % 更新theta1
    theta(2) = theta(2) - alpha * sum((feature * theta - result) .* feature(:,2)) / m;  % 更新theta2

    all_theta(:,i) = theta; % 将theta存储起来

end

本人也是刚刚学习机器学习，有什么问题欢迎指正，谢谢！