斯坦福大学机器学习笔记——特征和多项式回归以及正规方程

我们可以举一个例子来引入多项式回归：
比如我们之前遇到的房价问题，对于房价的影响我们假设有两个特征，一个是房子的宽度 $x_{1}$ ，另外一个是房子的长度 $x_{2}$ ，这针对房价的估测我们可以建立下面形式的假设：
$h_{\theta }(x)=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}$
但是我们可以换一个角度思考，我们完全可以用房子的面积 $x_{3}$ 作为特征来对房价进行估计，则房子的价格估计可以建立下面的假设：
$h_{\theta }(x)=\theta _{0}+\theta _{1}x_{3}$
所以我们在建立模型时，可以对一些特征进行选择，选择特征的不同所构建的假设不同。
但是我们经常见到的问题，并不是都是能够线性拟合的，比如下面的数据类型：
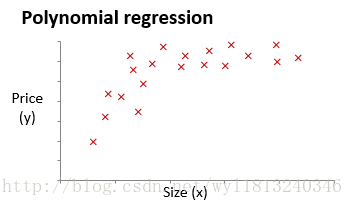
这里写图片描述
显然上面的数据使用线性拟合，拟合的效果不是特别好，同时若是我们选择下面形式的拟合方式：
$h_{\theta }(x)=\theta _{0}+\theta _{1}x+\theta _{2}x^{2}$
这个形式的拟合方式是二次函数，二次函数拟合上面的数据时，会在对称轴的右方出现下降的趋势，所以这种拟合方式也是不合理的，所以我们想到了用到的拟合方式为：
$h_{\theta }(x)=\theta _{0}+\theta _{1}x+\theta _{2}x^{2}+\theta _{3}x^{3}$
这种假设能够很好的拟合该数据类型。
对于使用什么形式的假设比较合适，通常我们需要先观察数据然后确定准备尝试怎样的模型，也就是说模型的确定是由数据来决定的。
上面提到的二次函数和三次函数拟合方式都可以称为多项式回归。
对于多项式的回归我们可以将其转化为线性回归的方式进行拟合，若我们另 $x_{1}=x,x_{2}=x^{2},x_{3}=x^{3}$ ,则：
$h_{\theta }(x)=\theta _{0}+\theta _{1}x+\theta _{2}x^{2}+\theta _{3}x^{3}=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+\theta _{3}x_{3}$
通过上述方式，我们将多项式回归问题转化为线性问题来求解。
注意：我们采用多项式回归时，前面博客讲到的特征缩放仍然是有必要的。

正规方程：
对于上面的线性回归算法我们都是采用的梯度下降法，使得损失函数最小，而对于线性回归算法还有另外一种使得损失函数最小的方法，那就是正规方程。
正规方程式通过求解下面的方程来找出使得代价函数最小的参数：
$\frac{\partial J(\theta _{j}))}{\partial\theta _{j} }=0$
假设我们的训练集特征矩阵为X（包含 $x_{0}=1$ ）并且训练集结果为向量y，利用正规方程可以解得参数 $\theta =（X^{T}X）^{-1}X^{T}y$
其中,T代表矩阵的转置，上标-1代表矩阵的逆运算。
举例来看一下正规方式的使用：
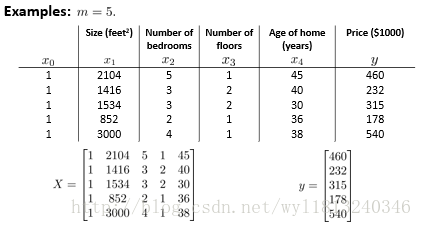
这里写图片描述
这就是上述每个矩阵的构建方式，然后带入公式就可以求得待求参数（一般针对矩阵化的编程语言，求逆一般都有现成的函数可以调用）。
从求取参数的式子中我们不难发现，当求待求的参数 $\theta$ 时，需要一个求逆的过程，但是不是所有的矩阵都有逆矩阵的，一般当出现下列情况四，矩阵不可逆：

特征之间不独立，比如在描述身高时，选取的两个特征为米和英尺，因为这两个之间存在着一种换算关系：1米(m)=3.2808399英尺(ft)，所以这两个特征不是独立的，这种情况下，矩阵是不可逆的。
当特征的数量大于训练集的数量时，正规方程也是不能用的。

当使用正规方程时：
1.首先确定是否有相关的特征，如果存在相关的特征，则去除相关特征；
2.当特征的数目较多时，可以去除一些不重要的特征，用少量的特征表示尽可能多的内容。
下面来比较一下梯度下降法和正规方程的优劣：
梯度下降法的优势：
1.当特征的数量比较大时（特征的数量超过10000），也能够很好的实现损失函数最小化，同时时间复杂度不是很高；而当特征的数量比较大时，使用正规方程求解逆运算是非常耗时的，所以此时使用梯度下降法比较合适。
2.梯度下降法适用于所有类型的模型，而正规方程的方法一般只适用于线性模型，不适合逻辑回归等其他模型。
正规方程的优势：
1.当特征点的数量不是很大时，使用正规方程更加简答，不需要像梯度下降算法一样迭代实现，一次计算就可以得出最优参数。
2.对于梯度算法来说，性能的好坏还与学习率的设置有关，学习率设置不合适，时间消耗较长，甚至得不到最优解，而正规方程的方法不需要学习率的设置。

基于python的正规方程实现如下所示：

import numpy as np

#从数据集中得到特征矩阵和标签向量
def loadDataSet(fileName):

    num_fea=len(open(fileName).readline().split(','))-1 #获得特征的数量
    fr=open(fileName)   #打开文件
    featureArr=[]
    labelArr=[]
    # 读取每一行的数据
    for line in fr.readlines():
        line_fea=[]
        line_data=line.strip().split(',')   #将每一行的数据按照','分隔开（使用什么分隔开看数据本身的构成）
        line_data.insert(0,'1') #将特征进行扩充，将特征矩阵转化为增广矩阵的形式
        for i in range(num_fea+1):
            line_fea.append(float(line_data[i]))    #得到每一行的特征

        featureArr.append(line_fea)
        labelArr.append(float(line_data[-1]))   #得到每一行的标签

    return featureArr,labelArr



def normalEquation(featureArr, labelArr):
    featureArr=np.mat(featureArr)
    labelArr=np.mat(labelArr).T

    xTx = featureArr.T*featureArr
    if np.linalg.det(xTx)==0:
        print("This matrix is singular, it can't do inverse")
        return
    ws=(xTx.I)*(featureArr.T*labelArr)
    return ws


#主程序
featureArr,labelArr=loadDataSet('ex1data2.txt')
ws=normalEquation(featureArr,labelArr)

print(ws)

matlab实现正规方程的代码如下：

clear;
close all;

%% 数据处理和初始化

data = load('ex1data2.txt'); % ex1data.txt中第一列是特征，第二列是标签
feature = data(:,1:end-1);    % 取出特征数据
result = data(:,end);  % 出标签数据  

[num_sample, num_feature] = size(feature);
feature = [ones(num_sample,1) feature];  % 将特征进行扩展，在原来的基础上增加一列全为1的矩阵

xTx = feature' * feature;

if det(xTx)==0
    sprintf('the matric is a singular, it can not do inverse!')
else
    theta = pinv(xTx) * feature' * result;
end

% 测试数据
test_data = [1520 4;5551 3];   %测试数据

[num_test_sample, num_test_feature] = size(test_data);  %测试数据的个数  
test_data = [ones(num_test_sample,1) test_data];  %测试数据的扩充
test_result = test_data * theta;    %测试数据的预测结果

test = feature * theta;

本人菜鸟一枚，有什么问题欢迎指正。

斯坦福大学机器学习笔记——特征和多项式回归以及正规方程

猜你喜欢